#AcWing：DP系列_acwing dp-优快云博客

本文深入探讨了动态规划(DP)在解决背包问题、完全背包、多重背包、线性DP、最长上升子序列、最长公共子序列、最短编辑距离等问题上的应用。通过实例解析了DP的状态转移方程，并展示了如何通过优化减少空间复杂度。同时，文章还介绍了区间DP、状态压缩DP在石子合并和蒙德里安梦想问题中的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

好气啊，每次遇到DP我就无可奈何了！听别人讲觉得好神奇，自己就不会做！行！那我今天就不干啥了（除了数据库PPT）就学这个DP，算是一个周末福利吧！
转一下y总写的，由数据范围反推算法复杂度，仔细琢磨吧，多刷题！
本周任务就是DP学习，加上leetcode练习dp
下周是搜索
在这里插入图片描述

1 背包问题

01背包

01背包是背包里面的物品最多只能选择一个，朴素的做法就是二维DP

f(i, j)表示只能选前i个物品且体积不超过j的最大值；
f(i,j) = max(f(i-1,j), f(i-1,j-v[i]) + w[i])

#include<bits/stdc++.h>
using namespace std;

const int N = 1010;
int V[N], W[N];
int f[N][N];

int main()
{
    int n, v;
    scanf("%d %d", &n, &v);
    for(int i = 1; i <= n; i++)
        scanf("%d %d", &V[i], &W[i]);
    
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= v; j++)
        {
            f[i][j] = f[i - 1][j];
            if(j >= V[i])
                f[i][j] = max(f[i][j], f[i - 1][j - V[i]] + W[i]);
        }
    }
    printf("%d", f[n][v]);
    return 0;
}

然后发现，f[i][j]只与前一个f[i - 1][j]有关，所以可以减少一维数组。但是就是f[j] = max(f[j], f[j - V[i]] + W[i]);需要确保f[j-V[i]]是i-1时候的不是i时候的，所以可以倒着遍历j

#include<bits/stdc++.h>
using namespace std;

const int N = 1010;
int V[N], W[N];
int f[N];

int main()
{
    int n, v;
    scanf("%d %d", &n, &v);
    for(int i = 1; i <= n; i++)
        scanf("%d %d", &V[i], &W[i]);
    
    for(int i = 1; i <= n; i++)
    {
        for(int j = v; j >= V[i]; j--)
            f[j] = max(f[j], f[j - V[i]] + W[i]);
    }
    printf("%d", f[v]);
    return 0;
}

完全背包

完全背包就是指物品的数量是无限的，其他一样。
哈哈哈哈哈哈今天学到了一个词，面向yxc编程，哈哈哈哈哈太对了！
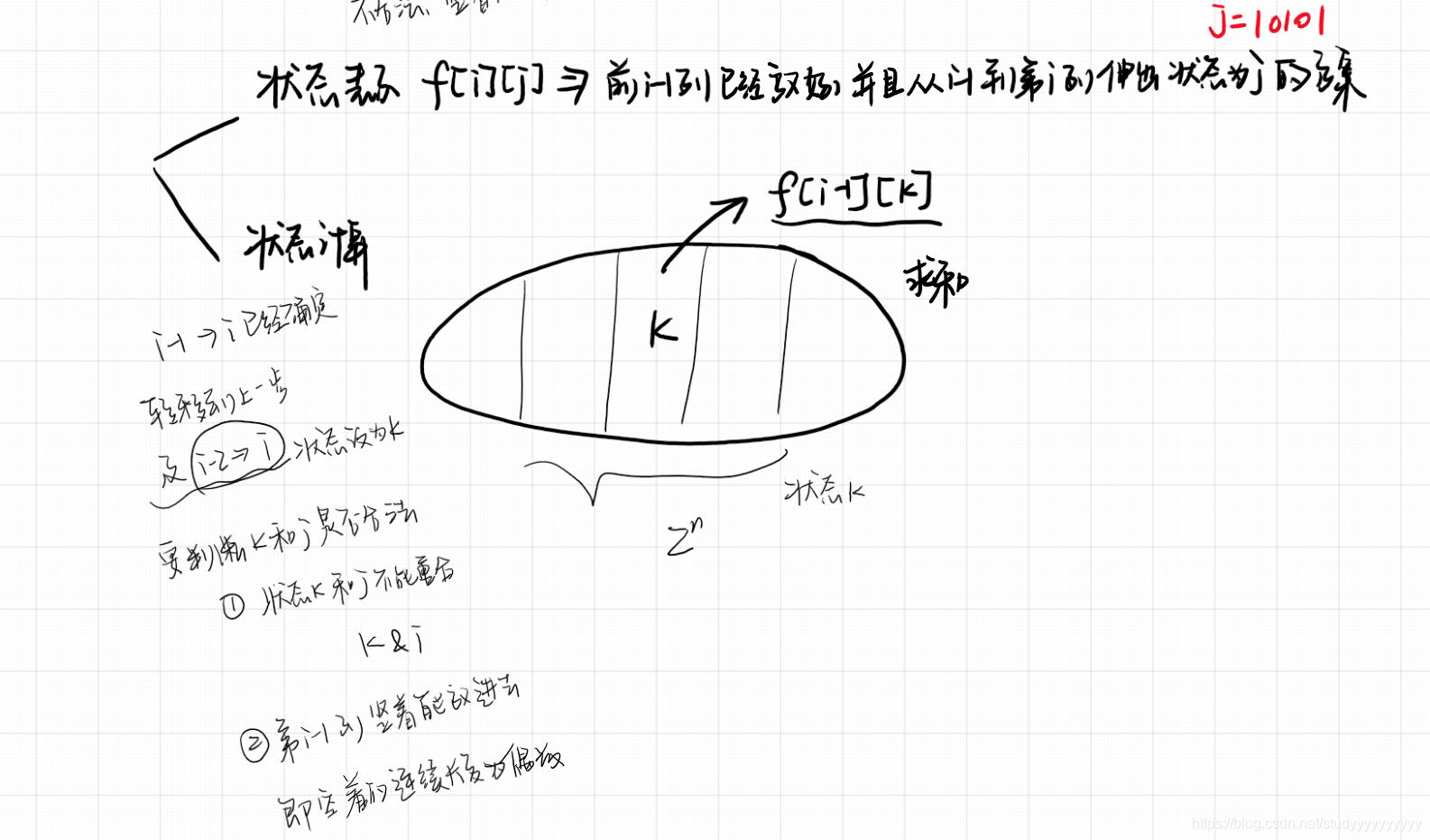
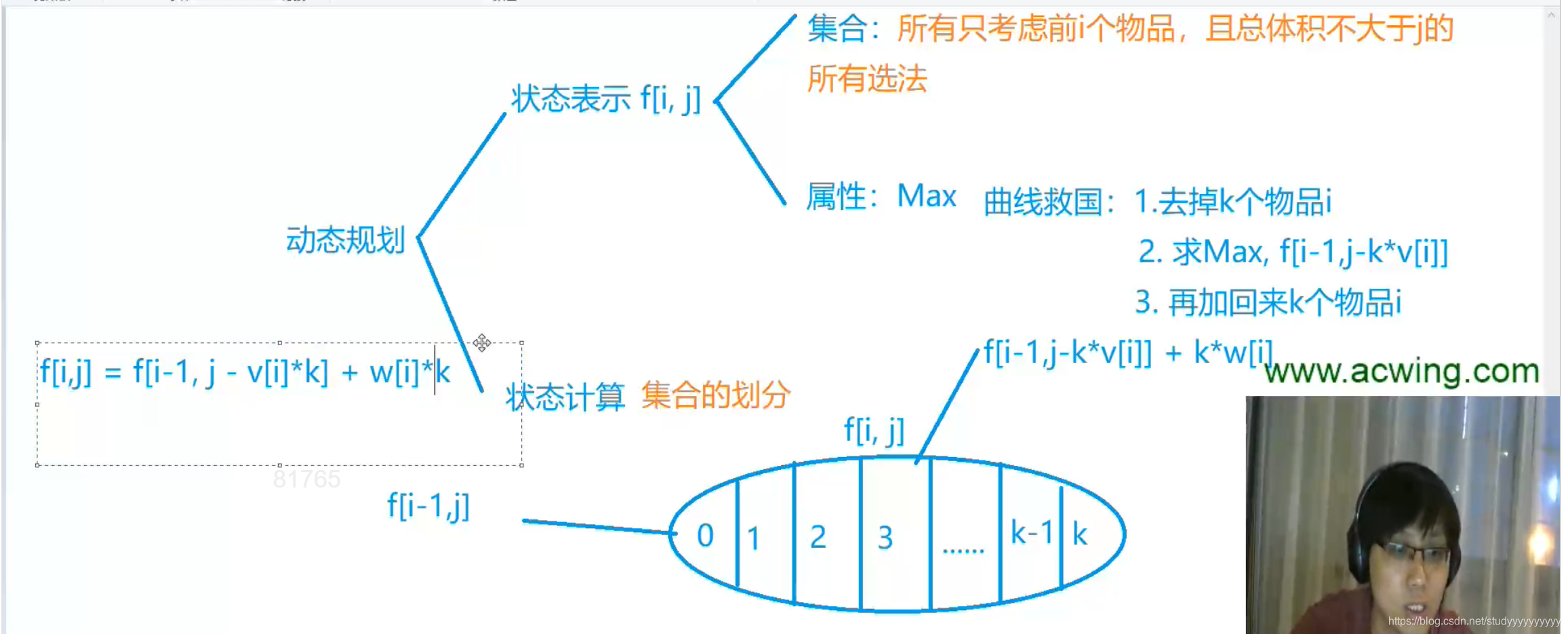在这里插入图片描述最朴素的完全背包，分成k个组，然后取每个组中最大的。

#include<bits/stdc++.h>
using namespace std;

const int N = 1010;
int v[N], w[N];
int f[N][N];

int main()
{
    int n, m;
    scanf("%d %d", &n, &m);
    for(int i = 1; i <= n; i++)
        scanf("%d %d", &v[i], &w[i]);
    
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            for(int k = 0; k * v[i] <= j; k++)
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
    
    printf("%d", f[n][m]);
    return 0;
}

经过推导发现可以将其降为二维
在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;

const int N = 1010;
int v[N], w[N];
int f[N][N];

int main()
{
    int n, m;
    scanf("%d %d", &n, &m);
    for(int i = 1; i <= n; i++)
        scanf("%d %d", &v[i], &w[i]);
    
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            f[i][j] = f[i - 1][j];
            if(j >= v[i])
                f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
        }
    }
        
    
    printf("%d", f[n][m]);
    return 0;
}

类似于01背包，变成一维。f[j] = max(f[j], f[j - v[i]] + w[i]);变成这个需要f[j - v[i]]是第i个物品时的i，而完全背包正是这样的，所以不用倒序遍历j，即可完成。

#include<bits/stdc++.h>
using namespace std;

const int N = 1010;
int v[N], w[N];
int f[N];

int main()
{
    int n, m;
    scanf("%d %d", &n, &m);
    for(int i = 1; i <= n; i++)
        scanf("%d %d", &v[i], &w[i]);
    
    for(int i = 1; i <= n; i++)
    {
        for(int j = v[i]; j <= m; j++)
        {
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        }
    }
        
    
    printf("%d", f[m]);
    return 0;
}

下面是我菜菜的笔记。。。
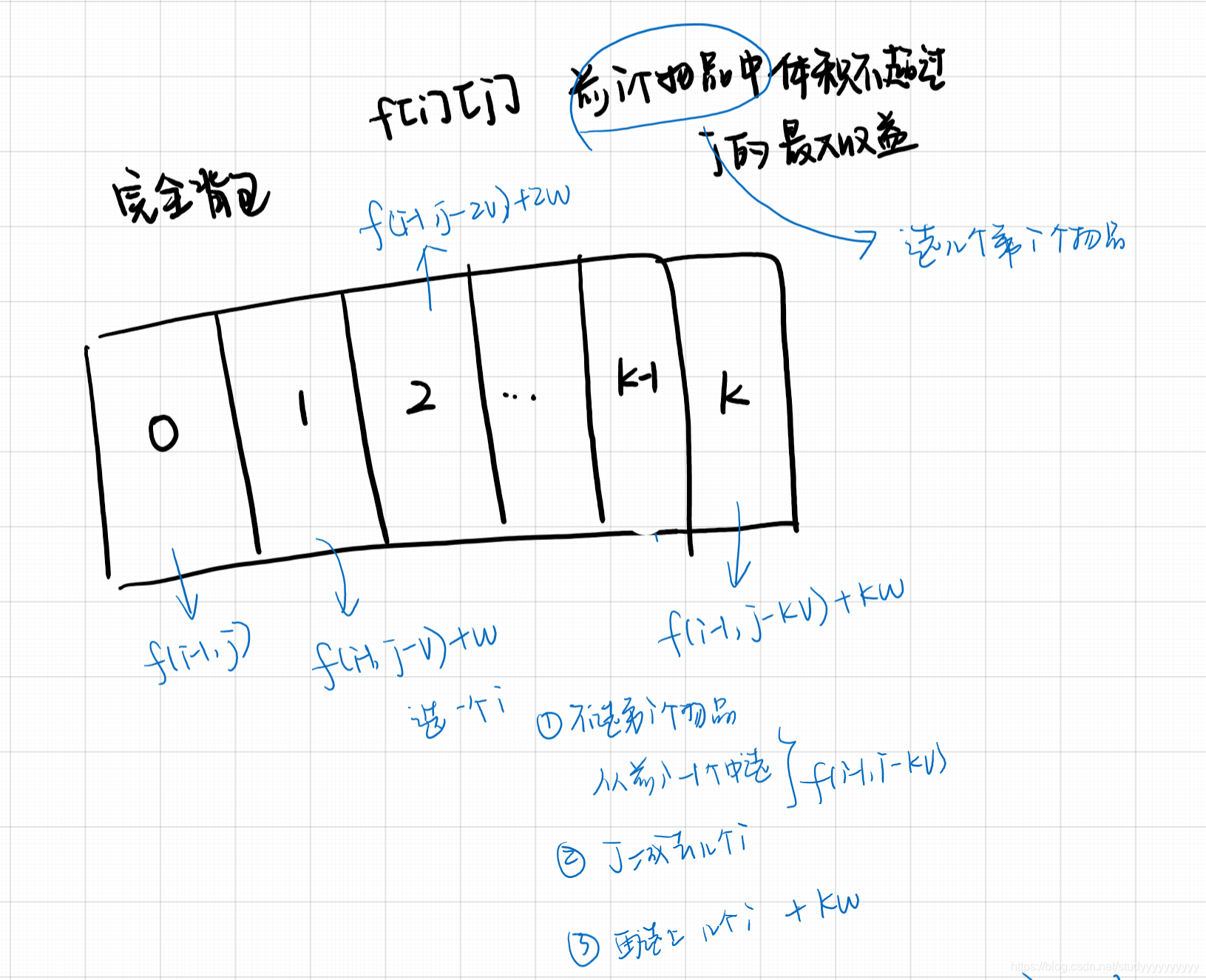
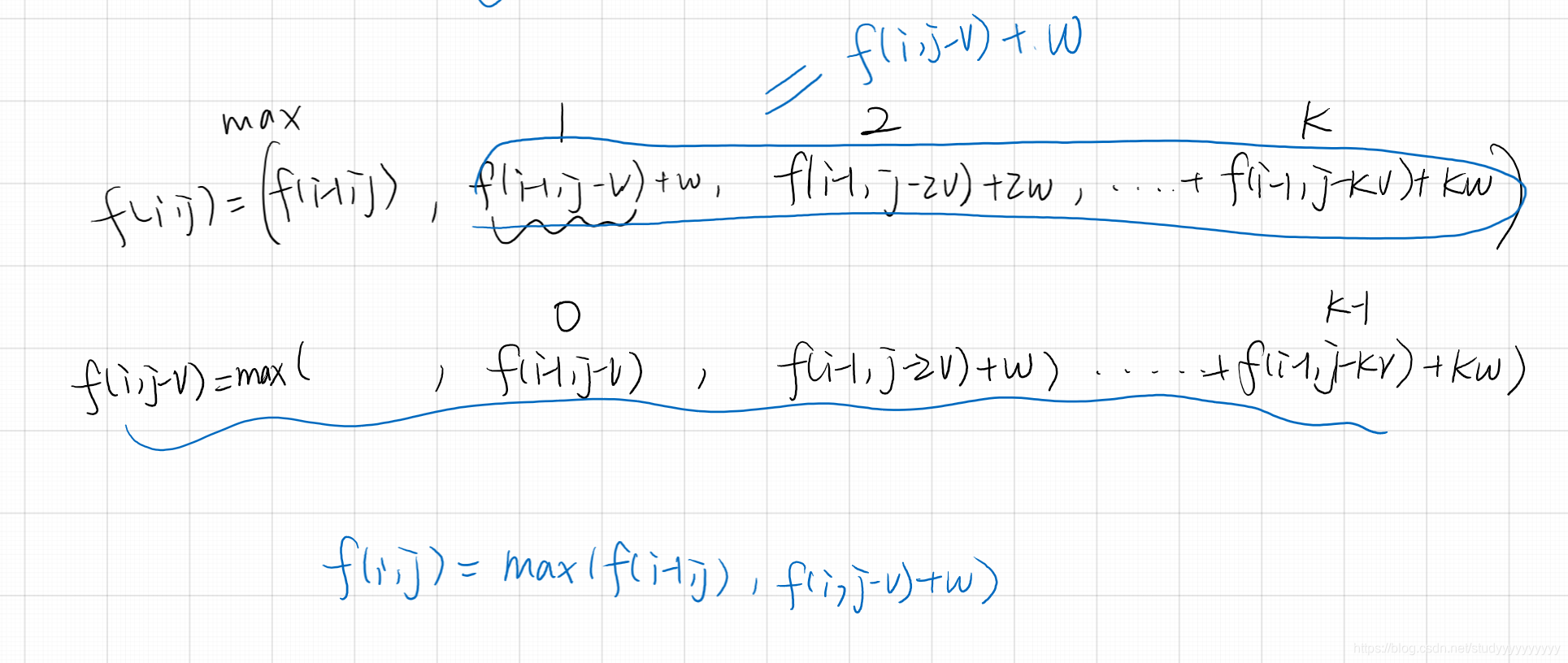
在这里插入图片描述

多重背包

多重背包既不是最多一个，也不是无限个，是有给定数量的。
朴素的就和完全背包相同，只需要再把他限制在s[i]之内就行。

#include<bits/stdc++.h>
using namespace std;

const int N = 110;

int v[N], w[N], s[N];
int f[N][N];

int main()
{
    int n, m;
    scanf("%d %d", &n, &m);
    for(int i = 1; i <= n; i++)
        scanf("%d %d %d", &v[i], &w[i], &s[i]);
    
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            for(int k = 0; k <= s[i] && k * v[i] <= j; k++)
            {
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
            }
        }
    }
    
    printf("%d", f[n][m]);
    return 0;
}

那个改进版的有点没太懂，脑子现在晕了，好困啊！

分组背包

2 线性DP

线性dp就是指计算的时候大概按照某个顺序计算.

数字三角形

首先是如何表示这个三角形,如何存储,大概就按照下面图上这样.
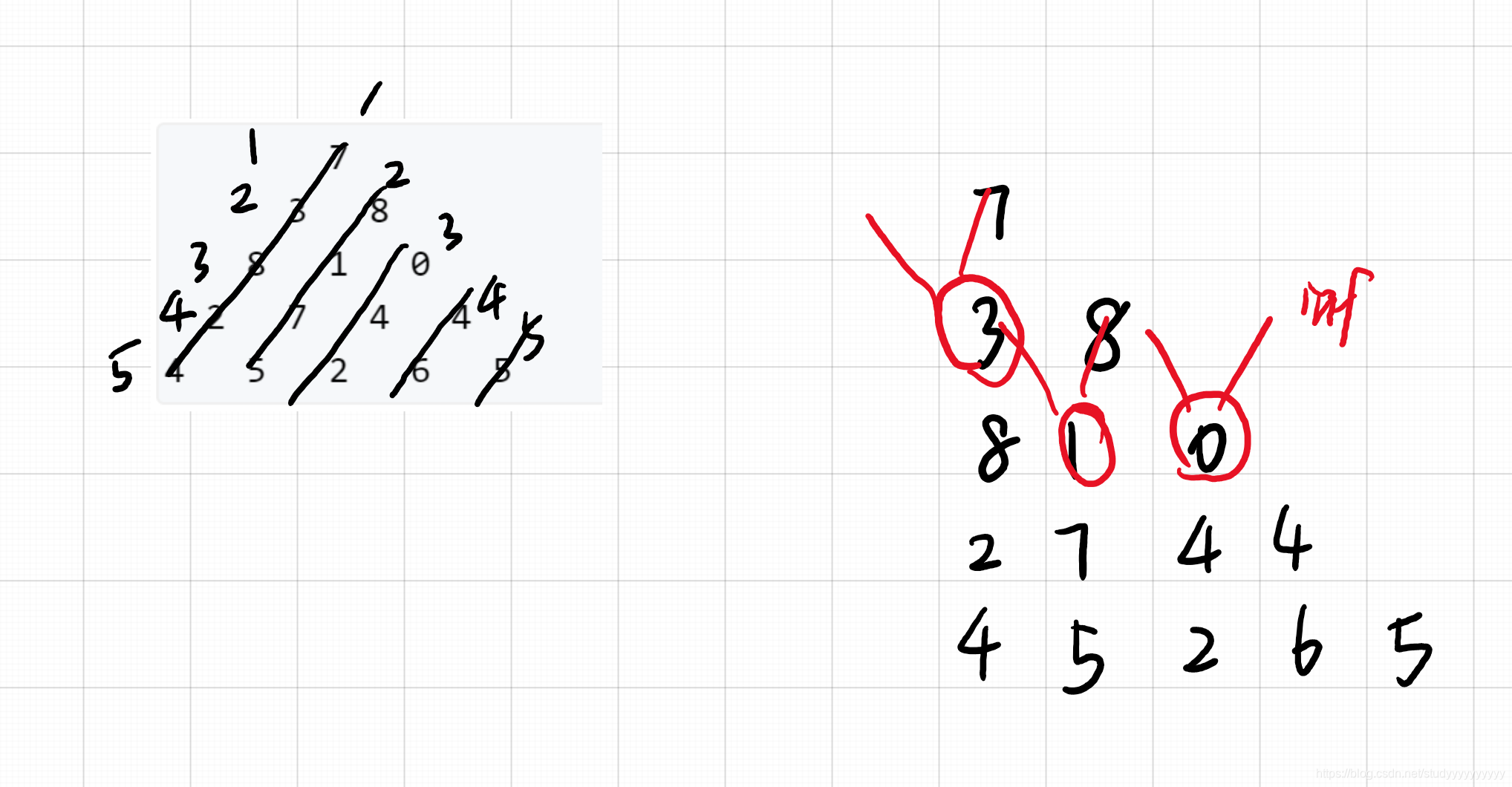
在这里插入图片描述

状态表示:f[i][j]表示到(i, j)这个点时最大路径和;
状态计算:f[i][j]这个点的最大值只取决于左上和正上那两个点的最大值,即f[i][j] = max(f[i - 1][j - 1], f[i - 1][j]) + a[i][j];
边界:列的左边要初始化,右边也要初始化一下,由于存在负值,初始化为INT_MIN

#include<bits/stdc++.h>
using namespace std;

const int N = 510;
int a[N][N];
int f[N][N];

int main()
{
    int n, ans = INT_MIN;
    scanf("%d", &n);
    
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= i; j++)
            scanf("%d", &a[i][j]);
            
    for(int i = 0; i <= n; i++)
        for(int j = 0; j <= n + 1; j++)
            f[i][j] = INT_MIN;
    
    f[1][1] = a[1][1];
    for(int i = 2; i <= n; i++)
        for(int j = 1; j <= i; j++)
            f[i][j] = max(f[i - 1][j - 1], f[i - 1][j]) + a[i][j];

            
    for(int i = 1; i <= n; i++)
        ans = max(ans, f[n][i]);
        
    printf("%d", ans);
    return 0;
}

也可以从最下面一层向上求,倒序dp,不用考虑边界(下面一层长)

#include<bits/stdc++.h>
using namespace std;

const int N = 510;
int a[N][N];
int f[N][N];

int main()
{
    int n, ans = INT_MIN;
    scanf("%d", &n);
    
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= i; j++)
            scanf("%d", &a[i][j]);
            
    
    for(int i = n; i >= 1; i--)
        for(int j = 1; j <= i; j++)
            f[i][j] = max(f[i + 1][j], f[i + 1][j + 1]) + a[i][j];
        
    printf("%d", f[1][1]);
    return 0;
}

也可以不用f,直接在a上进行加和.

#include<bits/stdc++.h>
using namespace std;

const int N = 510;
int a[N][N];

int main()
{
    int n, ans = INT_MIN;
    scanf("%d", &n);
    
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= i; j++)
            scanf("%d", &a[i][j]);
            
    
    for(int i = n; i >= 1; i--)
        for(int j = 1; j <= i; j++)
            a[i][j] = max(a[i + 1][j], a[i + 1][j + 1]) + a[i][j];
        
    printf("%d", a[1][1]);
    return 0;
}

最长上升子序列

首先，子序列和字串的概念分清楚。子序列就是从前面排着选就行了，不用非得连着。但是子序列就是得连续。

状态标志：f[i]表示以第i个数结尾的上升子序列中长度的最大值
状态计算：就是前面一个数字（可能是 1, 2, 3,… i - 1）再加上第i个数字，就是再前一个发f[j]上+1

在这里插入图片描述
代码很简单

#include<bits/stdc++.h>
using namespace std;

const int N = 1010;
int a[N], f[N];

int main()
{
    int n, ans = INT_MIN;
    scanf("%d", &n);
    for(int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    
    for(int i = 1; i <= n; i++)
    {
        f[i] = 1;
        for(int j = 1; j <i; j++)
        {
            if(a[i] > a[j])
                f[i] = max(f[i], f[j] + 1);
        }
    }
    for(int i = 1; i <= n; i++)
        ans = max(ans, f[i]);
    printf("%d", ans);
    return 0;
}

下面给出一个nlogn的算法，在上述基础上进行改进。
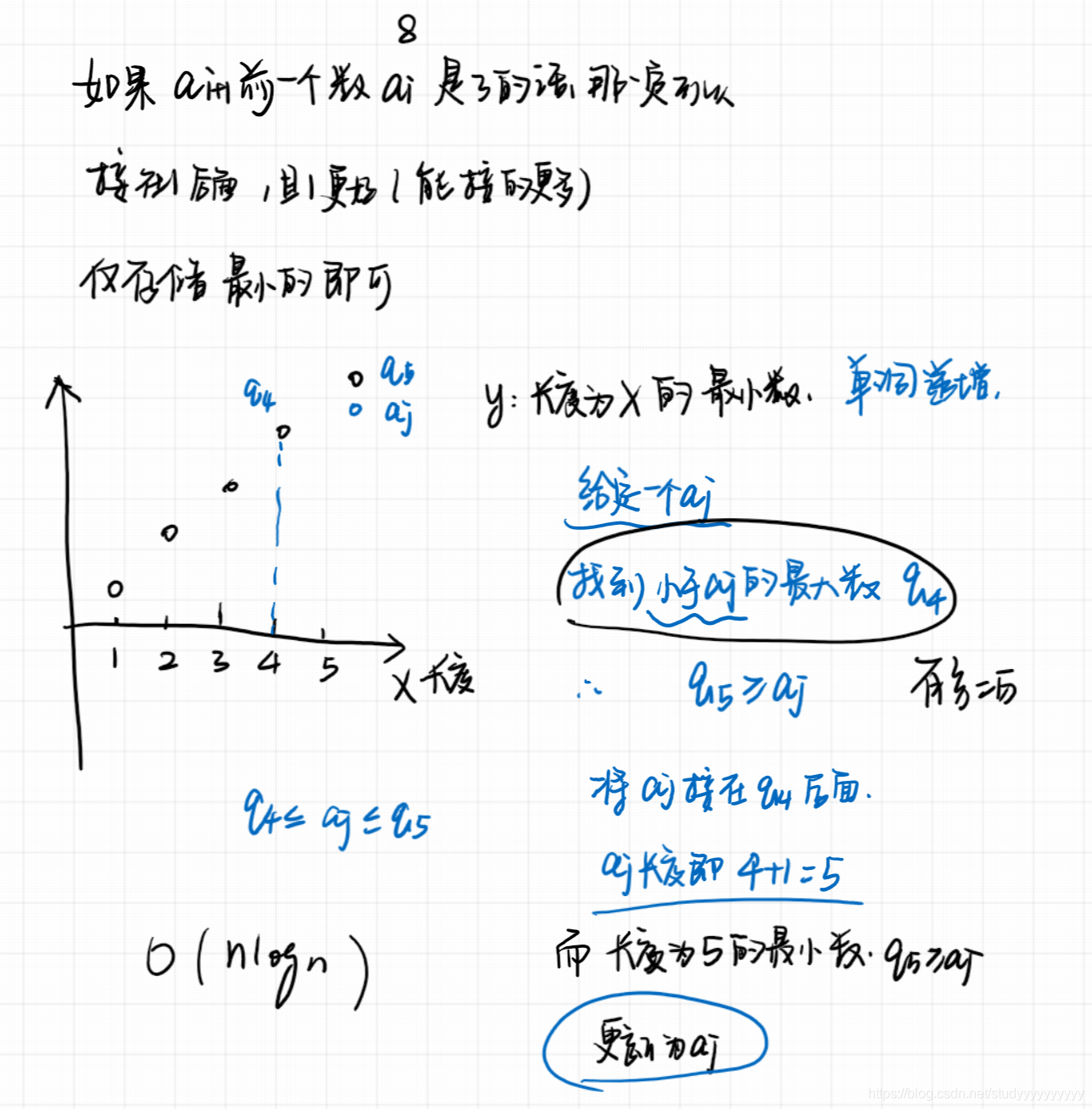
在这里插入图片描述
图总是裂了，不知道为啥。。。指路一个好的[题解]、(https://www.acwing.com/solution/content/6525/)
堆栈

#include<bits/stdc++.h>
using namespace std;

const int N = 100010;
int a[N];
int q[N];

int main()
{
    int n;
    scanf("%d", &n);
    for(int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    int len = 0;    //目前整个序列中的最长，也就是q中元素个数
    for(int i = 1; i <= n; i++)
    {
        int l = 0, r = len;
        while(l < r)
        {
            int mid = (l + r + 1) / 2;
            if(q[mid] < a[i]) l = mid;
            else r = mid - 1;
        }
        len = max(len, l+ 1);
        q[l + 1] = a[i];
    }
    printf("%d", len);
    return 0;
}

最长公共子序列

有点难，还没有完全理解
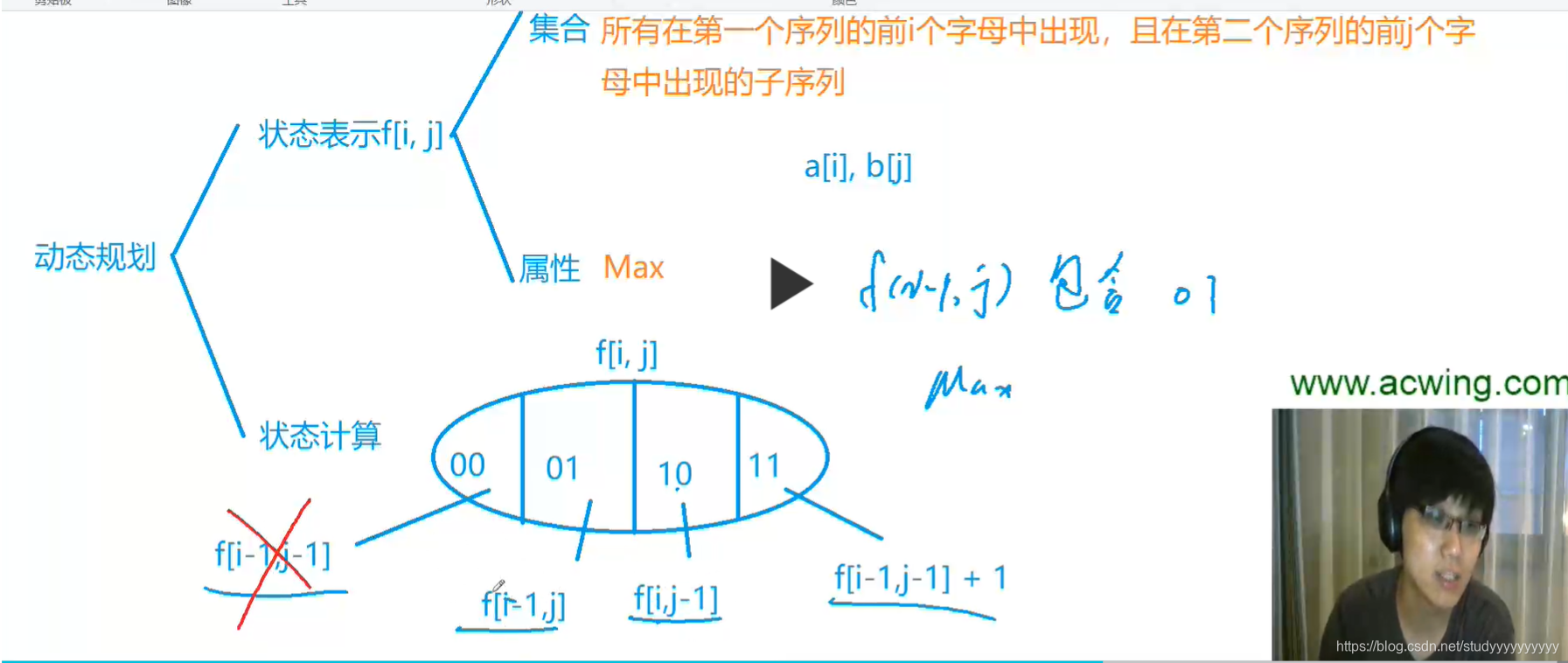
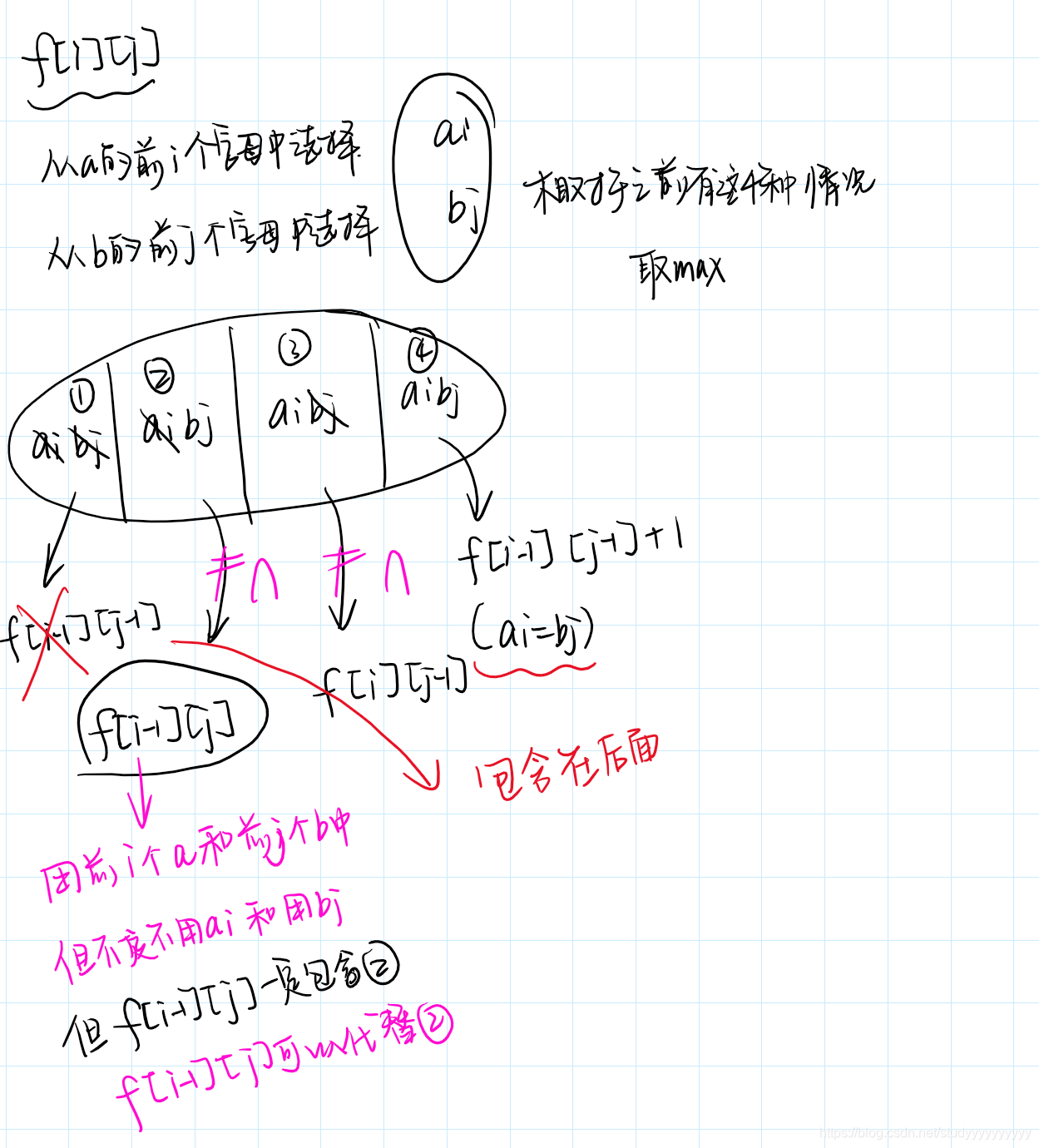
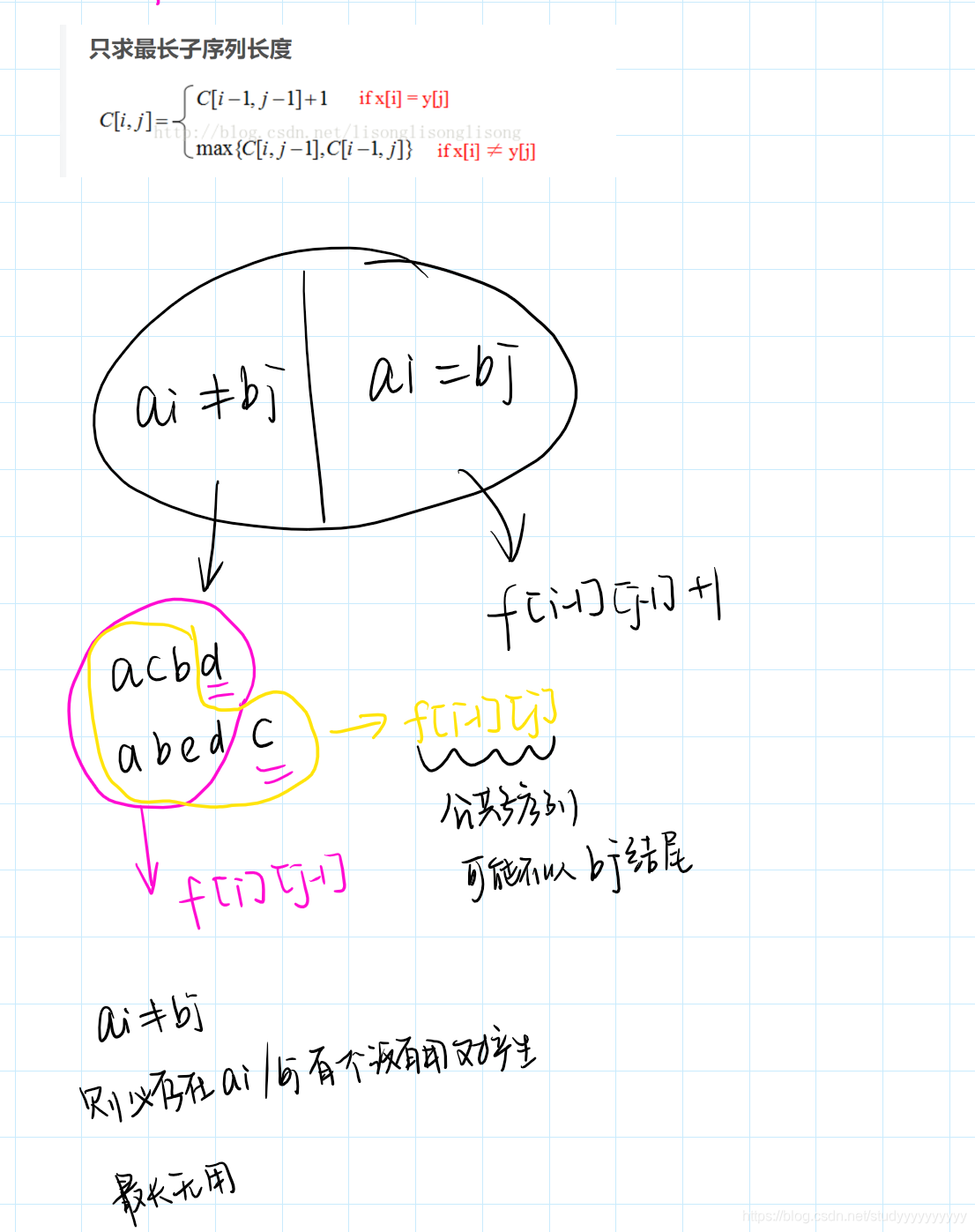
在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;

const int N = 1010;
char a[N], b[N];
int f[N][N];

int main()
{
    int n, m;
    scanf("%d %d", &n, &m);
    scanf("%s %s", a + 1, b + 1);
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            f[i][j] = max(f[i - 1][j], f[i][j - 1]);
            if(a[i] == b[j])
                f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);
        }
    }
    cout << f[n][m];
    return 0;
}

最短编辑距离

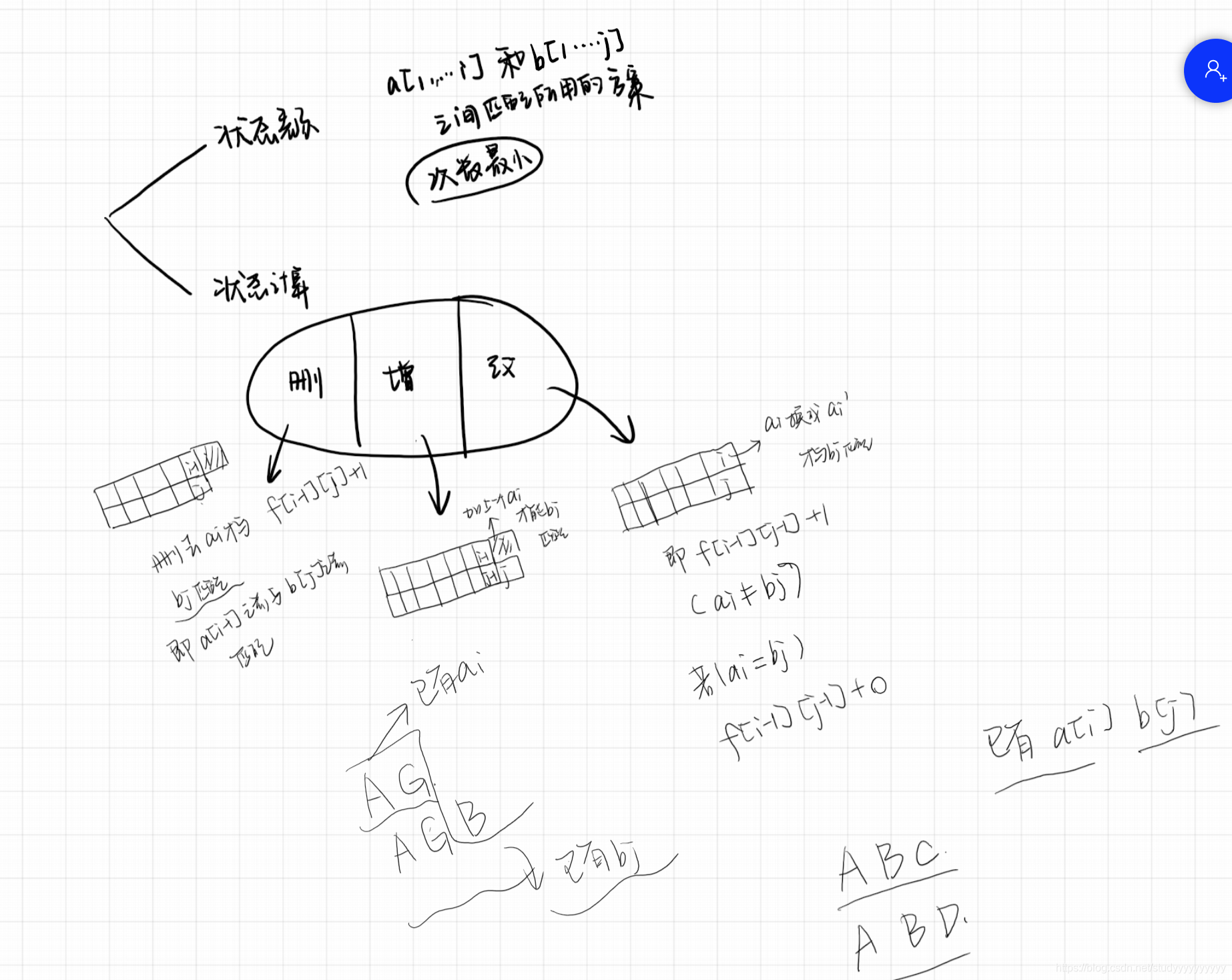
在这里插入图片描述
我写的关于增加的普遍理解:

我明白了! 同志们 !
状态表示是指a[1~ i]变成a[1~ j]也就是说已经有了a[1~ i]和b[1~ j]。举个例子:a数组是AGE,b数组是AGEF,此时i=3,j=4（从1开始）怎么变呢？就是在i后面加上一个F，不加F之前不就是应该要求1_i和1j-1相等嘛。
我们是受了i和j长度相等的影响，考虑的情况是a数组:AGF, b数组是AGE，此时i=3,j=3,再在i-1后面加上一个E，即要求1~ i和1~ j相等，这是不对的。你在i-1后面加上一个E，那这个序列就变成了AGEF和AGE，那么这个F怎么办呢？所以说是不对的。

#include<bits/stdc++.h>
using namespace std;

const int N = 1010;
char a[N], b[N];
int f[N][N];

int main()
{
    int m, n;
    scanf("%d %s", &m, a + 1);
    scanf("%d %s", &n, b + 1);
    
    //初始化
    for(int i = 0; i <= m; i++) f[i][0] = i;
    for(int i = 0; i <= n; i++) f[0][i] = i;
    
    
    for(int i = 1; i <= m; i++)
    {
        for(int j = 1; j <= n; j++)
        {
            f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1);
            if(a[i] != b[j])
                f[i][j] = min(f[i][j], f[i - 1][j - 1] + 1);
            else
                f[i][j] = min(f[i][j], f[i - 1][j - 1]);
        }
    }
    cout << f[m][n];
    return 0;
}

区间DP

石子合并

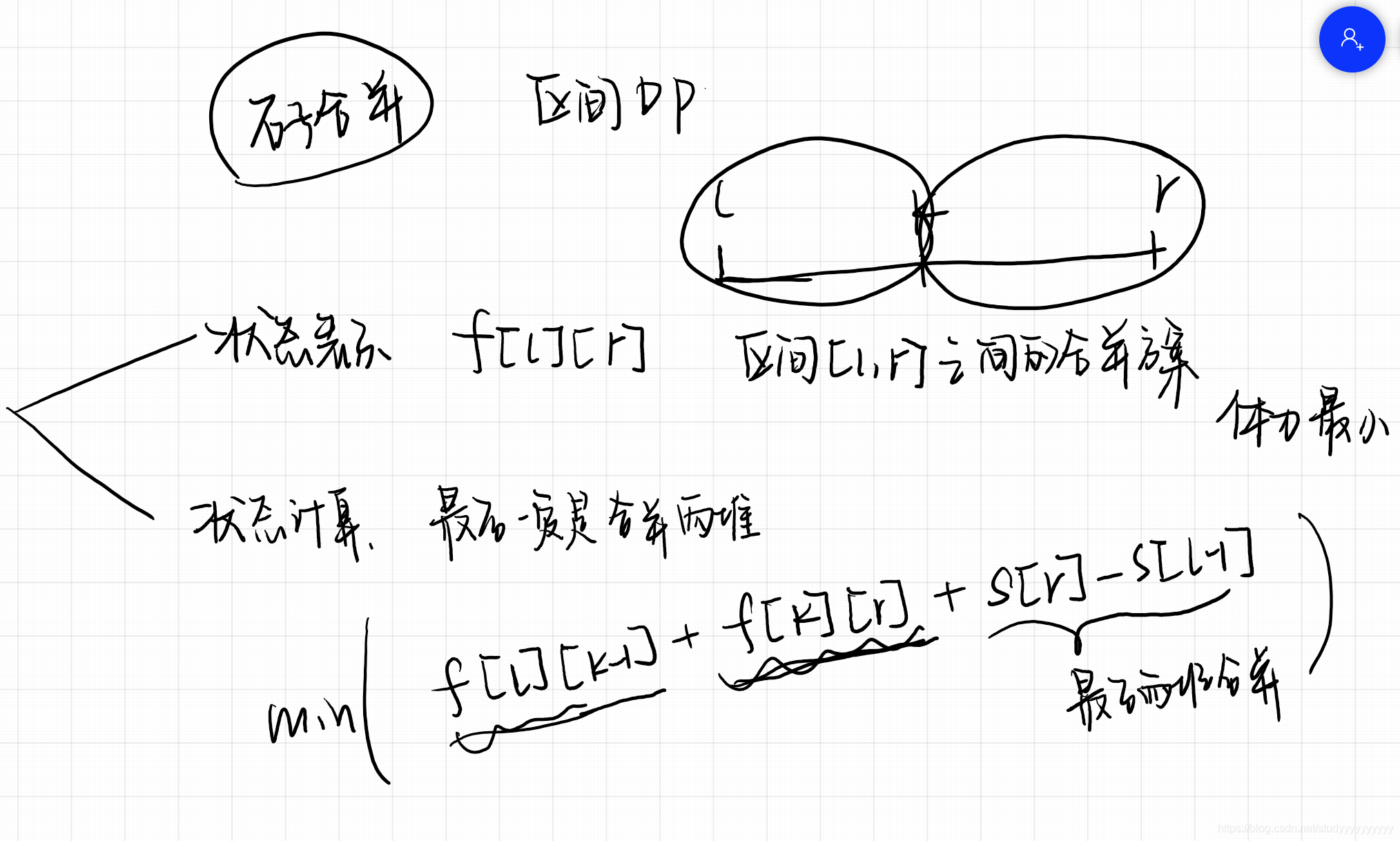
在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;

const int N = 310;
const int M = 1010;

int a[N];
int s[N];
int f[N][N];

int main()
{
    int n;
    scanf("%d", &n);
    for(int i = 1; i <= n; i++)
    {
        scanf("%d", &a[i]);
        s[i] = s[i - 1] + a[i];
    }
    
    for(int len = 2; len <= n; len++)
    {
        for(int i = 1; i + len - 1 <= n; i++)
        {
            int l = i, r = i + len - 1;
            f[l][r] = INT_MAX;
            for(int k = i; k < r; k++)
            {
                f[l][r] = min(f[l][r], f[i][k] + f[k + 1][r] + s[r] - s[i - 1]);
            }
        }
    }
    cout << f[1][n];
    return 0;
}

状态压缩DP

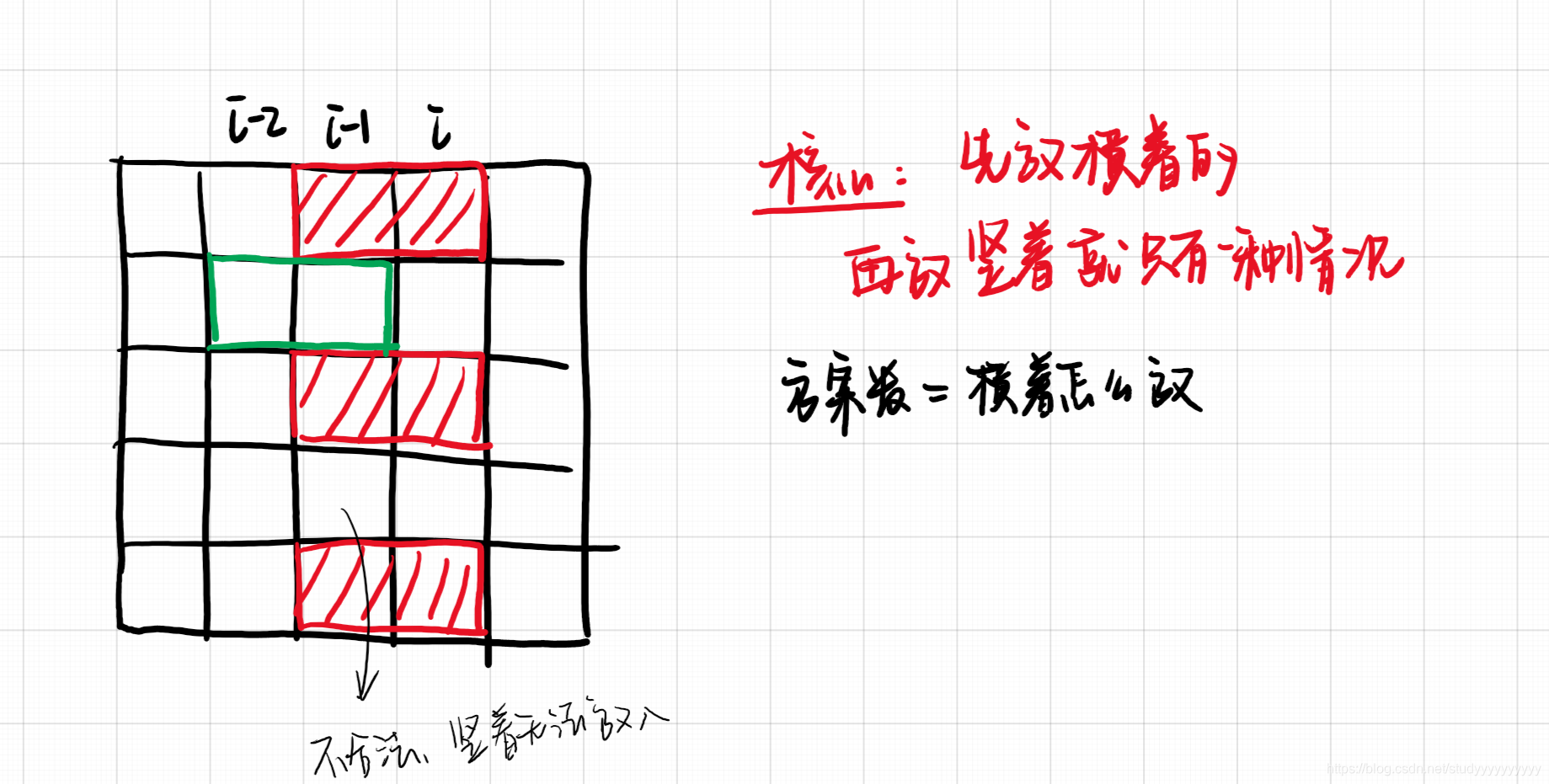
蒙德里安的梦想

在这里插入图片描述

详细题解

#include<bits/stdc++.h>
using namespace std;

const int N = 12;
const int M = 1 << N;

typedef long long LL;

LL f[N][M];
bool st[M];
vector<vector<int>> state(M);

int main()
{
    int n, m;
    cin >> n >> m;
    while(n != 0 && m != 0)
    {
        for(int i = 0; i < 1 << n; i++)
        {
            int cnt = 0;
            bool is_vaild = true;
            for(int j = 0; j < n; j++)
            {
                if((i >> j) & 1)
                {
                    if(cnt & 1)//奇数
                    {
                        is_vaild = false;
                        break;
                    }
                    else
                        cnt = 0;
                }
                else
                    cnt++;
            }
            if(cnt & 1)
                is_vaild = false;
            st[i] = is_vaild;
        }
        
        
        
        for(int j = 0; j < 1 << n; j++)
        {
            state[j].clear();
            for(int k = 0; k < 1 << n; k++)
            {
                if((j & k) == 0 && st[j | k])
                    state[j].push_back(k);
            }
        }
        
        memset(f, 0, sizeof f);
        
        f[0][0] = 1;
        
        for(int i = 1; i <= m; i++)
            for(int j = 0; j < 1 << n; j++)
                for(auto k : state[j])
                    f[i][j] += f[i - 1][k];
        cout << f[m][0] << endl;
        cin >> n >> m;
    }
}

最短哈密顿距离

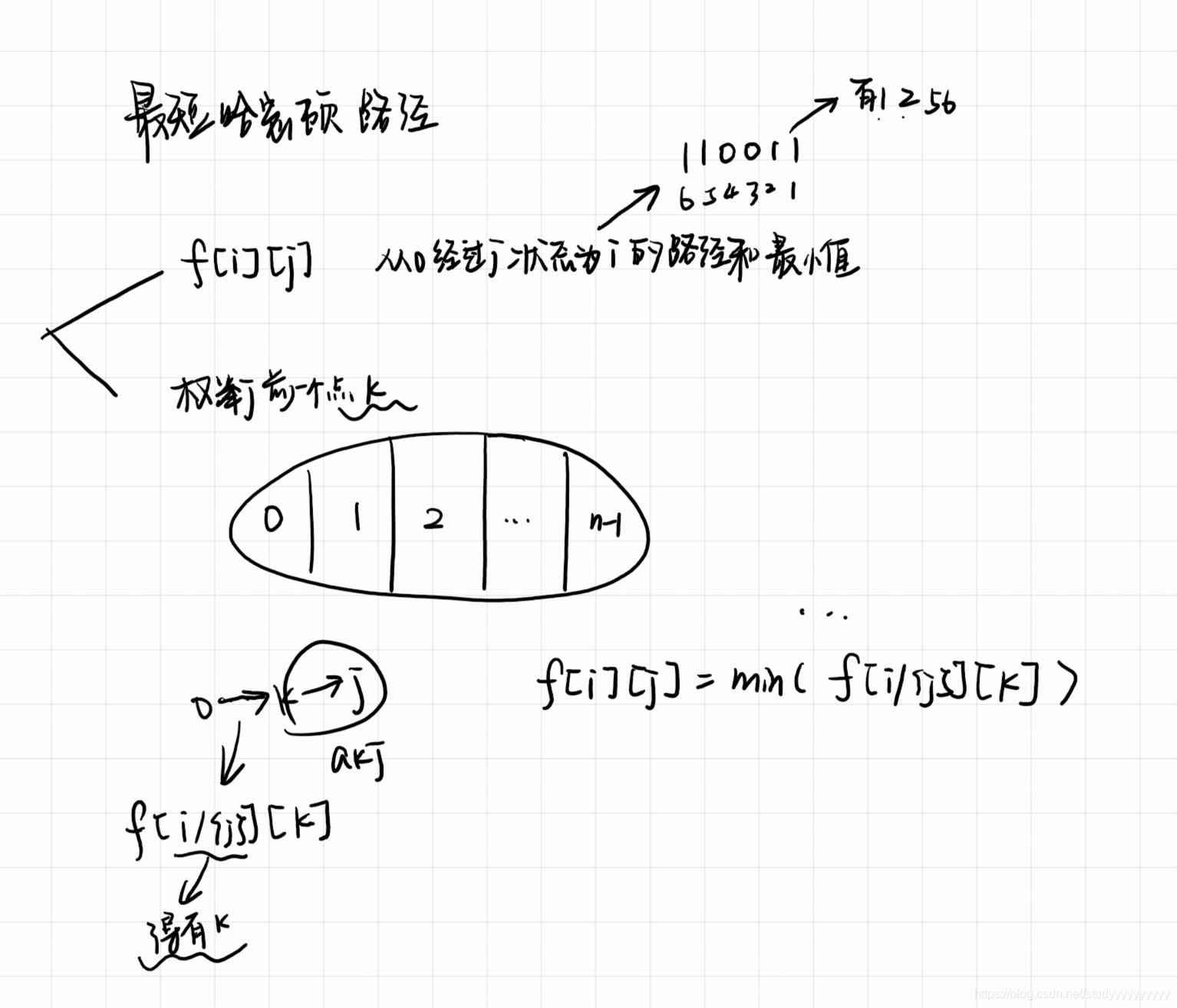
在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;

const int N = 20, M = 1 << N;
int a[N][N];
int f[M][N];

int main()
{
    int n;
    scanf("%d", &n);
    for(int i = 0; i < n; i++)
        for(int j = 0; j < n; j++)
            scanf("%d", &a[i][j]);
    
    memset(f, 0x3f, sizeof f);
    
    f[1][0] = 0;
    
    for(int i = 0; i < 1 << n; i++)
    {
        for(int j = 0; j < n; j++)
        {
            for(int k = 0; ((i >> j) & 1) && k < n; k++)
            {
                if((i - (1 << j)) >> k & 1)
                {
                    f[i][j] = min(f[i][j], f[i - (1 << j)][k] + a[k][j]);
                }
            }
            
        }
    }
    cout << f[(1 << n) - 1][n - 1];
    return 0;
}