机器学习入门（7）——神经网络的学习(Neural Networks: Learning)

代价函数（Cost Function）

反向传播算法（Backpropagation Algorithm）

为了计算代价函数的偏导数$\frac{\partial }{\partial {\Theta }_{ij}^{(l)}}J(\Theta )$，我们需要采用一种反向传播算法，也就是首先计算最后一层的误差，然后再一层一层反向求出各层的误差，直到倒数第二层。

首先用正向传播方法计算出每一层的激活单元，利用训练集的结果与神经网络预测的结果求出最后一层的误差，然后利用该误差运用反向传播法计算出直至第二层的所有误差。
我们的算法表示为：

反向传播算法的直观理解（Backpropagation Intuition）

• 前向传播算法：
  
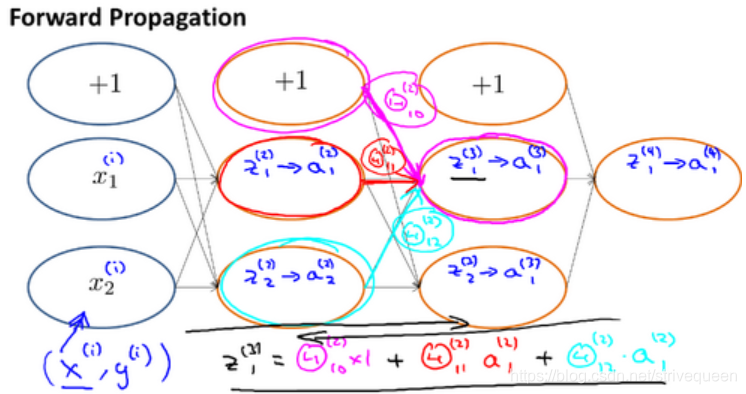
• 反向传播算法
  

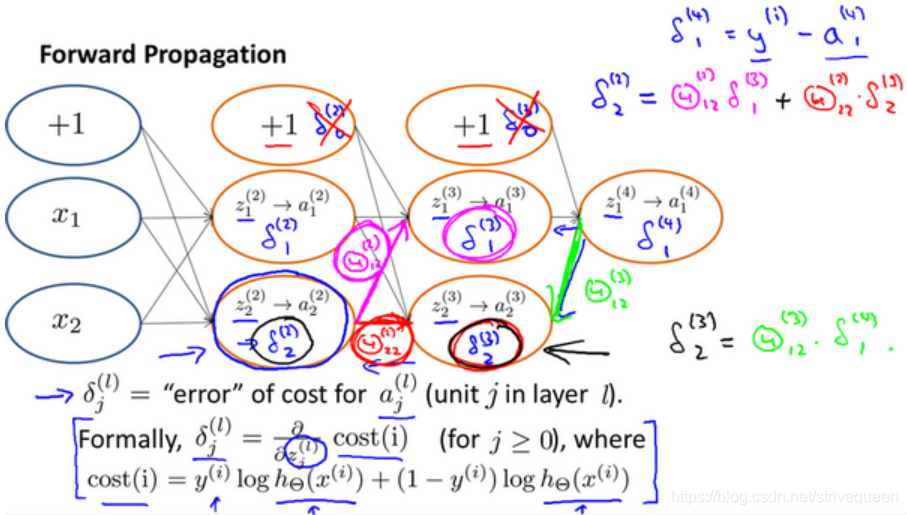
梯度检验（Gradient Checking）

对一个较为复杂的模型（例如神经网络）使用梯度下降算法时，可能会存在一些不容易察觉的错误。虽然代价看上去在不断减小，但最终的结果可能并不是最优解。
为避免这样的问题，我们采取一种叫做梯度的数值检验（Numerical Gradient Checking）方法，通过估计梯度值来检验我们计算的导数值是否真的是我们要求的。

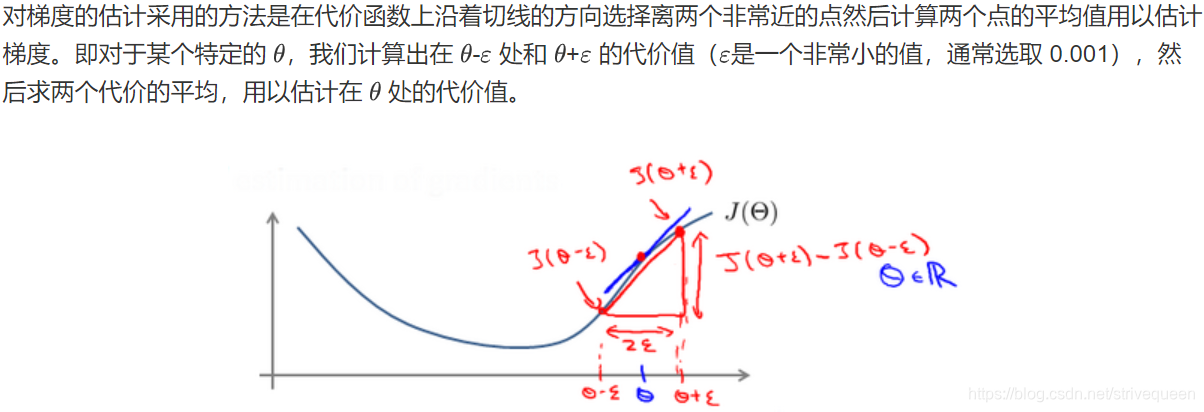
随机初始化（Random Initialization）

任何优化算法都需要一些初始的参数。初始所有参数为0的方法，对于逻辑回归来说是可行的，但是对于神经网络来说是不可行的。如果我们令所有的初始参数都为0，这将意味着我们第二层的所有激活单元都会有相同的值。同理，如果我们初始所有的参数都为一个非0的数，结果也是一样的。
因此，我们通常初始参数为±ε之间的随机值。

综合起来（Putting It Together）

使用神经网络时的步骤小结：

• 选择网络结构：即决定选择多少层以及决定每层分别有多少个单元。

1. 第一层的单元数即我们训练集的特征数量。
2. 最后一层的单元数是我们训练集的结果的类的数量。
3. 我们真正要决定的是隐藏层的层数和每个中间层的单元数。若隐藏层数大于1，确保每个隐藏层的单元个数相同，通常情况下隐藏层单元的个数越多越好。

• 训练神经网络：

1. 参数的随机初始化
2. 利用前向传播方法计算所有的$h_{\theta }(x)$
3. 编写计算代价函数 J的代码
4. 利用反向传播方法计算所有偏导数
5. 利用数值检验方法检验这些偏导数
6. 使用优化算法来最小化代价函数（梯度下降算法或更优化的方法）