1.1四种空间的定义AA
是m×nm×n的矩阵。
零空间N(A):n 维向量,是Ax=0Ax=0 的解,所以N(A)在RnRn里。
列空间C(A): 列向量是m维的,所以C(A)在RmRm里。
行空间C(AT)C(AT):A的行的所有线性组合,即A转置的列的线性组合(因为我们不习惯处理行向量C(AT)C(AT)在RnRn里。
A的左零空间N(AT)N(AT):A转置的零空间N(AT)N(AT)在RmRm里面。
1.2四种空间的维数四种空间的维数是多少?
列空间C(A):AA的主列就是列空间的一组基,,维数就是秩的大小。
行空间C(AT)C(AT) :dim(C(AT))=Rank(A)=rdim(C(AT))=Rank(A)=r,有一个重要的性质:行空间和列空间维数相同,都等于秩的大小。
零空间N(A):一组基就是一组特殊解,rr 是主变量的个数, 是自由变量的个数,零空间的维数等于n−rn−r,即dim(N(A))=n−rdim(N(A))=n−r。
左零空间N(AT)N(AT):矩阵ATAT有mm列,而其秩为rr,因此自由列数目为m−rm−r,所以dim(N(AT))=m−rdim(N(AT))=m−r。
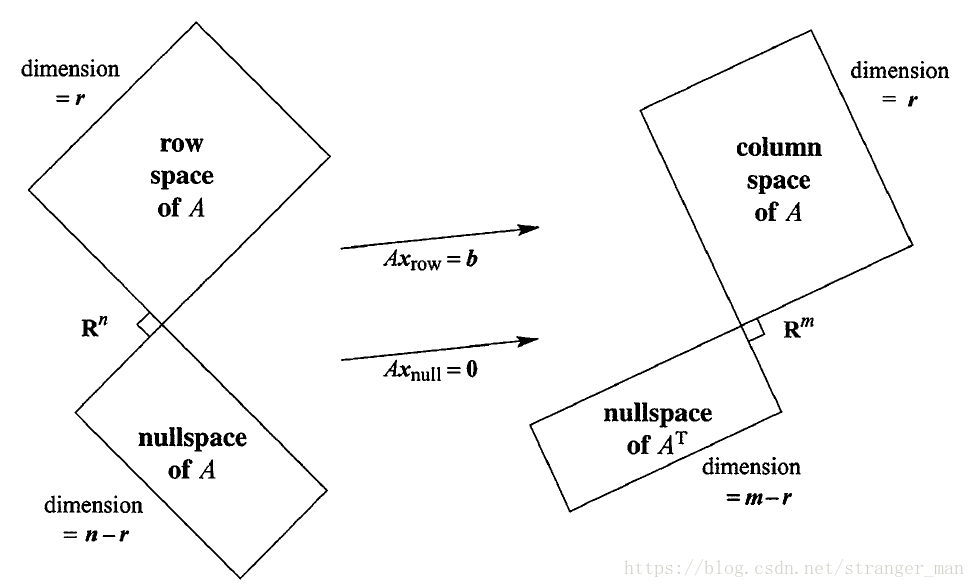
行空间和零空间在RnRn里,他们的维数加起来等于nn,列空间和左零空间在RmRm里,他们的维数加起来等于mm 。如下图所示:
2.正交(正交)向量和正交子空间(orthogonal subcpaces )2个正交向量,它们的点积为零。如有2个正交向量
vv 和 ,那么 vTw=0vTw=0. 知道了什么是正交向量,下面就是正交子空间的定义:
Subspace S is orthogonal to subspace T means: every vector in S is orthogonal to every vector in T
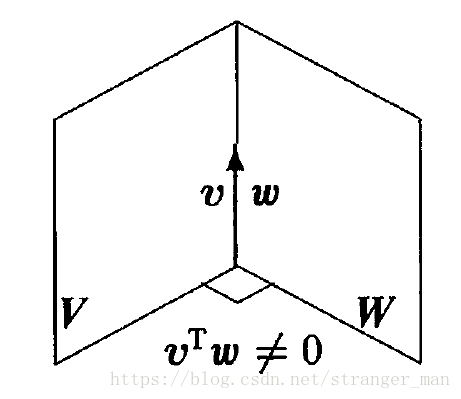
下图中有2个子空间,即2个平面V和W,这个2个子空间就不是正交的,虽然2个平面是垂直的,但是你会看到它们之间有个相交的线,而这条直线中的向量即属于V又属于W,它们平行却不垂直,因此V和W不是正确的。因此一个人和你说有1个向量在2个正交的子空间中,那么这个向量一定是零向量,因为只有它才垂直它本身,非零向量是不可能做到这一点的。
前面的图已经展示了四个子空间间的正交关系,这里我只解释一下为什么零空间和行空间是正交的? 实际上只要根据 Ax=0 就能得出这样的结论了。由于 Ax=0,那么矩阵的每个行向量乘以 x 都会等于0,如下图所示。有一个问题,之前说过我们既可以用行来表示线性变化也可以用列来表示线性变换,这里怎么只与行空间正交呢?其实我们在做矩阵化简的时候AA与其行最简形式的列空间是不相同的,这样研究的时候就不能用列空间来看啦。

为啥叫左零空间呢?
AT×y=0AT×y=0,将等式左右两边都转置,得:yT×A=0TyT×A=0T,如下,所以叫左零空间。

但我们一般还是习惯用ATy=0ATy=0,因为希望yy 是列向量。
所以,求矩阵的左零空间,就试着寻找一个产生零行向量的行组合,求矩阵的零空间,就试着寻找一个产生零列向量的列组合。
那么如何求解这个左零空间呢?
考虑我们前面学过的Gauss-Jordan消元法,我们在矩阵后面加一个单位阵:
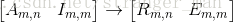
这样单位矩阵Im,mIm,m记录了AA的行变换过程。也就是说我们必然存在一个矩阵可以通过作用于来得到它的行最简形式,那么这个矩阵是谁呢?其实就是Em,mEm,m,因为Em,mIm,m=Em,mEm,mIm,m=Em,m。所以来看下面这个变换的例子:

观察RR中第三行为零行,相应的中的第三行也为左零空间的一组基[−1,0,1][−1,0,1]。即
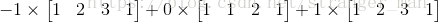





















 6148
6148

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








