算法-堆（堆排序）

今天我们来进行堆的学习，主要了解堆的基本结构、基本功能实现，还有如何手写堆。

堆的基本结构：

堆是一颗完全二叉树。
堆满足的性质（下面都是以小根堆为例）：
每一个节点都是小于左右子节点的（所以根节点是最小值）。
对于堆的存储：
存在一维数组中，1为根节点，x的左子树节点为2x，x的右子树节点为2x+1
由于下面调整成小根堆或者大根堆需要进行向上/下调整的操作，所以在这里一并介绍：
1.往下调整：

down(x){
* 把某个值改变，变大——>向下操作（因为是小根堆），不断和左右子树进行比较，如果左右子树中存在值比改变值小，就把较小值与改变值交换，否则，不动
* }

2.往上调整：

up(x){
* 把某个值改变，变小——>向上操作（因为是小根堆），不断和左右子树进行比较，如果左右子树中存在值比改变值大，就把较大值与改变值交换，否则，不动
* }

如何手写一个堆？

堆的功能实现：

1.插入一个数
2.求集合中的最小值
3.删除最小值
4.删除任意一个元素
5.修改任意一个元素

功能如何实现？

• 1.插入操作：
  堆的最后一个位置加上x：heap[++size] = x
  不断上移：up(size);
• 2.求集合中最小值
  heap[1];
• 3.删除最小值
  让最后一个位置的数覆盖第一个位置上的数，size–，再进行下沉（down(1)）操作
  原因：数组中删除头非常困难，但是删除尾部却很简单
  heap[1] = heap[size];
  size–;
  down(1);
• 4.删除任意一个元素
  heap[k] = heap[size];
  size–;
  down(k);
  up(k);（up和down只会执行一个）
• 5.修改任意一个元素
  heap[k] = x;
  down(k);
  up(k);

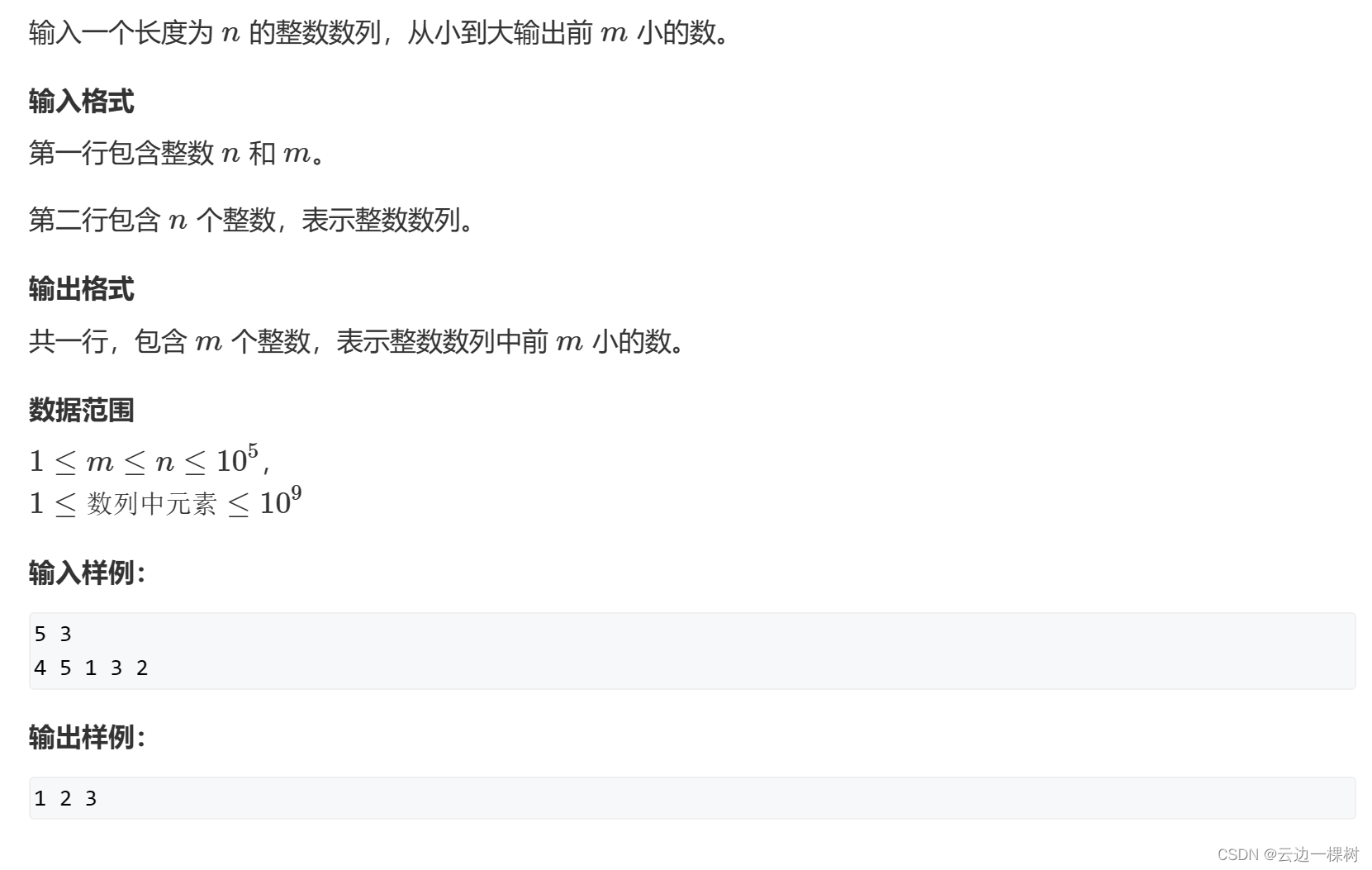
题目：

题解完整代码（Java）

import java.util.Scanner;

public class 堆 {
    static int N = 100010;
    static int heap[] = new int[N];
    static int size;//当前数组存有值的长度
    static int n;
    static int m;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        m = sc.nextInt();
        for (int i = 1; i <= n; i++) {
            heap[i] = sc.nextInt();
            size = n;
        }
        for (int i = n/2; i >= 1; i--) {//复杂度降到O(n)
            down(i);
        }
        while (m-- > 0){
            System.out.print(heap[1]+" ");
            heap[1] = heap[size];
            size--;
            down(1);
        }
    }

    public static void down(int u){//u是元素的下标
        //前两个if条件判断的逻辑是：由于不知道左右子树是否都存在，所以如果左子树存在的话，先比较放在根节点的当前元素值和左子树的值相比，找到小的那一个；如果有右子树的话，再把刚才找的小的那一个与右子树的值相比，找到最小的那个，再进行下沉操作
        int t = u;//分身变量t
        //u*2——>左子树的下标。如果左子树存在并且左子树的值比当前元素值小，就让分身变量t为左子树的下标
        if(u * 2 <= size && heap[u*2] < heap[t]){
            t = u * 2;
        }
        //u*2+1——>右子树的下标。如果右子树存在并且右子树的值比当前元素值要小，就让分身变量t为右子树的下标
        if(u * 2+1 <= size && heap[u*2+1] <heap[t]){
            t = u* 2 + 1;
        }
        //分身变量t的作用是——>记录之前比较最小值的位置的下标，与当前元素下标相比，如果u!=t证明当前根节点不是最小值，需要进行交换，保证根节点是最小值
        if(u != t){
            int temp = heap[t];
            heap[t] = heap[u];;
            heap[u] = temp;
            down(t);//由于小规模子树的有序并不能保证在改变数值之后大规模子树有序，所以要递归实现每一次的下沉，确保为小根堆。
        }
    }
}

堆主要了解基本结构，实现的功能并可以进行实现，应用举例为堆排序。