提升方法（下）提升树

提升方法采用加法模型（即基函数的线性组合）与前向分步算法。以决策树为基 函数的提升方法称为提升树（boosting tree）。对分类问题决策树是二叉分类树，对回归 问题决策树是二叉回归树。在AdaBoost的案例中看到的基本分类器x<v或x>v，可以看作是由一个根 结点直接连接两个叶结点的简单决策树，即所谓的决策树桩（decision stump）。

提升树 模型可以表示为决策树的加法模型：

提升树算法：

提升树算法采用前向分步算法。首先确定初始提升树f 0(x)＝0，第m歩的模型是：

 

其中，fm-1(x)为当前模型，通过经验风险极小化确定下一棵决策树的参数Θm， 

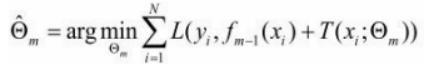
下面讨论针对不同问题的提升树学习算法，其主要区别在于使用的损失函数不同。包 括用平方误差损失函数的回归问题，用指数损失函数的分类问题，以及用一般损失函数的 一般决策问题。

对于二类分类问题，提升树算法只需将AdaBoost算法中的基本分类器限制为二类 分类树即可，可以说这时的提升树算法是AdaBoost算法的特殊情况，这里不再细述。下面 叙述回归问题的提升树。

 

回归问题提升树使用以下前向分步算法： 

在前向分步算法的第m步，给定当前模型fm-1(x)，需求解：