Kahn’s algorithm for Topological Sorting

Origin:

https://www.geeksforgeeks.org/topological-sorting-indegree-based-solution/

Topological sorting for Directed Acyclic Graph (DAG) is a linear ordering of vertices such that for every directed edge uv, vertex u comes before v in the ordering. Topological Sorting for a graph is not possible if the graph is not a DAG.

For example, a topological sorting of the following graph is “5 4 2 3 1 0?. There can be more than one topological sorting for a graph. For example, another topological sorting of the following graph is “4 5 2 0 3 1″. The first vertex in topological sorting is always a vertex with in-degree as 0 (a vertex with no in-coming edges).

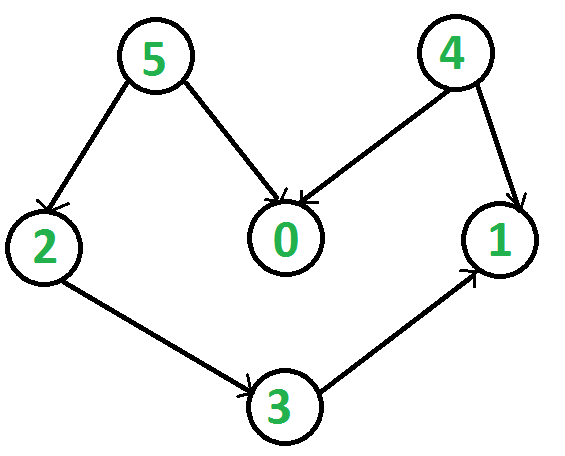
In this article we will see another way to find the linear ordering of vertices in a directed acyclic graph (DAG). The approach is based on the below fact :

A DAG G has at least one vertex with in-degree 0 and one vertex with out-degree 0.

Algorithm:
Steps involved in finding the topological ordering of a DAG:

Step-1: Compute in-degree (number of incoming edges) for each of the vertex present in the DAG and initialize the count of visited nodes as 0.

Step-2: Pick all the vertices with in-degree as 0 and add them into a queue (Enqueue operation)

Step-3: Remove a vertex from the queue (Dequeue operation) and then.

1. Increment count of visited nodes by 1.
2. Decrease in-degree by 1 for all its neighboring nodes.
3. If in-degree of a neighboring nodes is reduced to zero, then add it to the queue.

Step-4: Repeat Step 3 until the queue is empty.

Step-5: If count of visited nodes is not equal to the number of nodes in the graph then the topological sort is not possible for the given graph.