动态规划精讲-优快云博客

本文链接：https://blog.youkuaiyun.com/stdio_54456153/article/details/102841777

本文主要参考自《算法导论》

动态规划

动态规划方法通常用来求解最优化问题。这类问题可以有很多可行解，每个解都有一个值，我们希望寻找具有最优值的解。我们称这样的解为问题的一个最优解，而不是最优解，因为可能有多个解都达到最优值。

需要注意的是，动态规划是求解某类问题的一种方法，是考察问题的一种途径，而不是一种特殊的算法。

动态规划的求解步骤如下：

1. 刻画一个最优解的结构特征
2. 递归地定义最优解的值
3. 计算最优解的值，通常采用自底向上的方法
4. 利用计算出的信息构造一个最优解。

动态规划运用要求：

最优子结构：一个问题的最优解包含其子问题的最优解。
重叠子问题：问题的递归算法会反复地求解相同的子问题。

下面来看个最简单的例子：

裴波那契数列：

1，1，2，3，5，8……
从第三项开始，每一项等于前两项之和，现在要求该数列的第 n 项。（虽然这个求的不是最优解，但解题思路与动态规划相似，可以从此入门）

我们可以很快得到下面这样的递归示意图， $F i b (n) = F i b (n - 1) + F i b (n - 2)$ ：

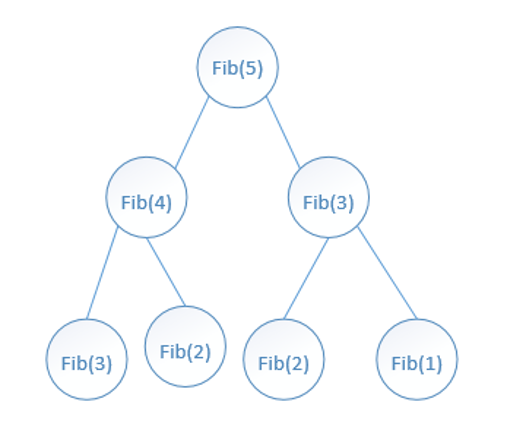
由此可以写出下面的代码：

long Fibonacci(int n) {
    if (n == 0)
        return 0;
    else if (n == 1)
        return 1;
    else
        return Fibonacci(n - 1) + Fibonacci(n-2);
}

这是最简单粗暴的方法，最大的问题就在于会进行大量的重复计算，看示意图我们就可以看到，Fib(3) 和 Fib(2) 就重复计算了两次，如果 n 再大一些，那么要重复计算的数据就将呈指数增长，这是我们不愿看到的。

下面这个解法就避开了重复计算的问题，其对应的动态规划解法是自底向上法（下面的数组 arr 对应着动态规划中的 DP 数组，放在这里只是为了跟动态规划对接一下，DP 数组存的是各个阶段的状态）。

int* Fibonacci(int n) {
	int arr[n] = {1,1};
    if (n <= 2)
        return 1;
    else {
        long num1 = 1;
        long num2 = 1;
        for (int i = 2;i < n - 1;i++) {
            num2 = num1 + num2;
            num1 = num2 - num1;
        	arr[i] = num2;
        }
        arr[i] = num2 + num1;
        return arr;
    }
}

arr 从第一项开始，存储了到第 n 项的每个裴波那契数列的值，这是动态规划解决方法中的自底向上的解法，其中 arr 对应着动态规划中的 DP 数组，用来存储各个阶段的最优解，关于 DP 数组，看到下面的题目会有一个更直观的认识。

钢条切割

假设有一家出售钢条的公司，其中钢条的价格表如下：

现有一个长度为 n 英寸的钢条，该如何切割使得销售收益最大？

问题分析：

如果一个最优解将钢条切割为 k 段，那么最优切割方案 $n=i_1+i_2+...+i_k$ ，得到的最大收益为：
$r_n=p_{i1}+p_{i2}+...+p_{ik}$

对于 $n \geq 1$ ， $r_n=max(p_n,r_1+r_{n-1},r_2+r_{n-2},r_3+r_{n-3},...,r_{n-1}+r_{1})$ ，其中 $p_n$ 对应不切割，对于每个 $i = 1, 2, . . ., n - 1$ ，首先将钢条切割为长度为 $i$ 和 $n - i$ 的两段，接着求解这两段的最优切割收益 $r_i$ 和 $r_{n-i}$ （每种方案的最优收益为两段的最优收益之和）。对该式子进行整理可得：

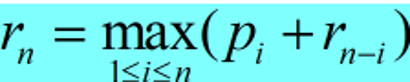
由此可得如下的伪代码：

CUT-ROD( p, n )
    if  n == 0
        return 0
    q= -∞
    for  i = 1 to n
        q = max(q, p[i]+CUT-ROD( p , n-i ))        
    return q

其中 p 为价格数组，n 为钢管长度，q 即为 $r_n$ 。

以上便为该题的最为直观的也是计算量十分巨大的解法。

我们看一下该解法的递归示意图，每个节点代表的是钢条的剩余长度：

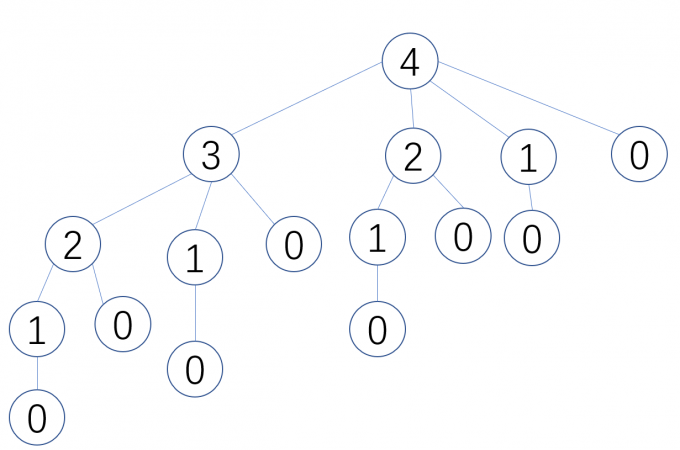
我们可以看到，就像第一个例子裴波那契数列一样，它对 2，3，1 节点进行了大量的重复计算，属于重叠子问题，而且根据分析我们也可以知道，要求他的最大收益，就要求他的子问题的最大收益，它属于最优子结构，因此可以使用动态规划。

带备忘的自顶向下法：此方法仍按自然的递归形式编写过程，但过程会保存每个子问题的解，通常保存在数组中，当需要一个子问题的解时，过程首先检查是否已经保存过此解，如果是，则直接返回保存的值，否则，按通常方式计算这个子问题。
自底向上法：这种方法一般需要恰当定义子问题 “规模” 的概念，使得任何子问题的求解都只依赖于 “更小的” 子问题的求解。因而我们可以将子问题按规模排序，按由小到大的顺序进行求解。当求解某个子问题时，他所依赖的那些更小的子问题都已求解完毕，结果已经保存。每个子问题只需求解一次，当我们求解他时，他的所有前提子问题都已求解完成。

对应的伪代码：
方法1：

MEMOIZED-CUT-ROD( p, n )
    if  r[n] >= 0              //判断长度为 n 的钢条的最大收益 r[n] 是否已经算出，其中没算出的都为负数
        return r[n]
    if  n == 0
        q=0
    else q= -∞
        for  i=1 to n
            q=max ( q, p[i]+MEMOIZED-CUT-ROD( p , n-i ) ) 

    r[n]=q       
    return q

方法2：

BOTTOM-UP-CUT-ROD( p, n )
    let r[0..n] be a new array
    r[0]=0
    for  j=1 to n               //计算钢条长度从 0 到 n 的所有最优解
        q= -∞
        for i=1 to j                     //对应递归式，其中前提子问题已经解出存放在数组 r 中
            q=max ( q, p[i]+r[j-i])       
        r[j]=q    
    return r[n]