行列式：定义、性质与计算详解-优快云博客

本文是学习笔记、知识分享性质，较多内容引用了相关书籍中的知识、图片等内容，目的只是记录学习笔记，无任何商业用途。如果您对本站所载文章及作品版权的归属存有异议，请及时告知。

本文链接：https://blog.youkuaiyun.com/static_eye/article/details/112306475

文章目录

行列式

行列式

行列式的定义与性质

本质定义（第一种定义）

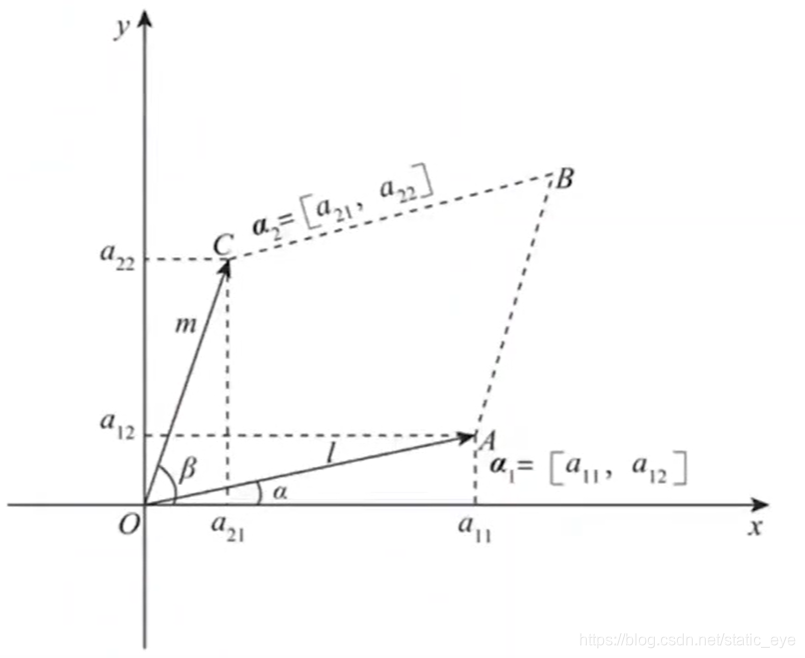
2阶行列式是由两个2维向量组成的，其（运算规则的）结果为以这两个向量为邻边的平行四边形的面积
$S_{OABC}=l \cdot m \cdot sin(\beta-\alpha)$
3阶行列式是由三个3维向量 $\mathbf{\alpha_1}=\left[ a_{11}, a_{12}, a_{13} \right], \mathbf{\alpha_2}=\left[ a_{21}, a_{22}, a_{23} \right], \mathbf{\alpha_3}=\left[ a_{31}, a_{32}, a_{33} \right]$ 组成的，其（运算规则的）结果为以这三个向量为邻边的平行六面体的体积
n阶行列式是由n个n维向量 $\mathbf{\alpha_1}=\left[ a_{11}, a_{12}, \cdots , a_{1n} \right], \mathbf{\alpha_2}=\left[ a_{21}, a_{22}, \cdots , a_{2n} \right], \cdots, \mathbf{\alpha_n}=\left[ a_{n1}, a_{n2}, \cdots, a_{nn} \right]$ 组成的，其（运算规则的）结果为以这n个向量为邻边的n维图像的体积。

性质

性质1：行列互换，其值不变，即 $\left|A\right|=\left|A^T\right|$ .
性质2：行列式中某行（列）元素全为零，则行列式为零.
性质3：行列式中某行（列）元素有公因子 $\neq 0)$ ，则 $k$ 可提到行列式外面，即
$\left| \begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n} \\ \vdots & \vdots & & \vdots \\ ka_{i1} & ka_{i2} & \cdots & ka_{in} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{array} \right| = k \left| \begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n} \\ \vdots & \vdots & & \vdots \\ a_{i1} & a_{i2} & \cdots & a_{in} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{array} \right|$

$k\left|A \right|$ 乘进去只乘一行或一列
该性质也叫“倍乘”性质

性质4：行列式中某行（列）元素均是两个元素之和，则可拆成两个行列式之和，即
$\left|A\right|=\left|A^T\right|$ .
性质2：行列式中某行（列）元素全为零，则行列式为零.
性质3：行列式中某行（列）元素有公因子 $\neq 0)$ ，则 $k$ 可提到行列式外面，即
$\left| \begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n} \\ \vdots & \vdots & & \vdots \\ a_{i1}+b_{i1} & a_{i2}+b_{i2} & \cdots & a_{in}+b_{in} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{array} \right| = \left| \begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n} \\ \vdots & \vdots & & \vdots \\ a_{i1} & a_{i2} & \cdots & a_{in} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{array} \right| + \left| \begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n} \\ \vdots & \vdots & & \vdots \\ b_{i1} & b_{i2} & \cdots & b_{in} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{array} \right|$

该性质也叫单行（列）可拆/加性

性质5：行列式中两行（列）互换，行列式的值反号。

也称为“互换”性质

性质6：行列式中两行（列）元素相等或对应成比例，则行列式为零
性质7：行列式中某行（列）的 $k$ 倍加到另一行（列），行列式的值不变

该性质也叫“倍加”性质

互换，倍乘，倍加——三个初等变换。矩阵篇会正式提出这三个初等变换（矩阵的初等变换）

逆序数法定义（第二种定义）

排列和逆序
排列由 $n$ 个数 $\cdots, n$ 组成的一个有序数组称为一个 $n$ 级排列，如 $23145$ 是一个5级排列， $41352$ 也是一个5级排列，n级排列共有 $n!$ 个
逆序在一个n级排列 $i_1i_2 \cdots i_s \cdots i_t\cdots i_n$ 中，若 $i_s > i_t$ ，且 $i_s$ 排在 $i_t$ 前面，则称这两个数构成一个逆序.
逆序数 一个排列中，逆序的总数称为该排列的逆序数，记作 $\tau(i_1i_2\cdots i_n)$ ，如 $\tau(231546)=3, \tau(621534)=8$ . 由小到大顺排的排列称为自然排序，如 $12345$ ，显然，自然排序的逆序数为0.
奇排列和偶排列 排列的逆序数为奇数时，该排列称为奇排列；排列的逆序数为偶数时，该排列称为偶排列。
n阶行列式的定义
$n(n\ge 2)$ 阶行列式
$\left| \begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{array} \right| = \sum_{j_1j_2 \cdots j_n}(-1)^{\tau(j_1j_2\cdots j_n)}a_{1j_1}a_{2j_2}\cdots a_{nj_n}.$
这里 $\sum_{j_1j_2 \cdots j_n}$ 表示对所有n个列下标排列求和，故为 $n!$ 项之和。注意到行下标已经顺排，而列下标是任一个n级排列，故每项由取自不同行、不同列的n个元素的乘积组成，每项的正负号取决于 $(-1)^{\tau(j_1j_2\cdots j_n)}$ . 当列下标为奇排列时，应附加负号；当列下标为偶排列时，应附加正号.

作为练习，求一下如下行列式：
$\left| \begin{array}{cccc} 5 & 2 & 1 \\ 1 & 2 & 5 \\ 34 & 1 & 34 \\ \end{array} \right| = ？$
$\left| \begin{array}{cccc} 我&0&生\\ 0&有&0\\ 你&0&幸\\ \end{array} \right| = ？$

行列式的展开定理（第三种定义）

阶数超过3的行列式，若还用前面两种定义来求，就太麻烦了，为此，提出行列式的展开定理

余子式
在n阶行列式中，去掉元素 $a_{ij}$ 所在的第 $i$ 行、第 $j$ 列元素，由剩下的元素按原来的位置与顺序组成的 $n - 1$ 阶行列式称为元素 $a_{ij}$ 的余子式，记作 $M_{ij}$ .
代数余子式
余子式 $M_{ij}$ 乘 $1)^{i+1}$ 后称为 $a_{ij}$ 的代数余子式，记作 $A_{ij}$ ，即
$A_{ij}=(-1)^{i+1}M_{ij}$
行列式按某一行（列）展开的展开公式
以按行展开为例：
$\left| A\right| = \sum_{j=1}^na_{ij}A{ij} (i=1,2,\cdots,n)$

几个重要的行列式

主对角线行列式（右上（左下）三角形行列式）

直接对角线元素相乘即可

副对角线行列式（左上（右下）三角行列式）

副对角线元素相乘，前面加上系数 $(-1)^{\frac {n(n-1)}{2}}$
$(-1)^{\frac {n(n-1)}{2}}a_{1n}a_{2,n-1}\cdots a_{n1}$

拉普拉斯行列式
分块矩阵的行列式, $A$ 为m阶矩阵， $B$ 为n阶矩阵，则
$\left| \begin{array}{cccc} A & O \\ O & B \end{array}\right| = \left| \begin{array}{cccc} A & C \\ O & B \end{array}\right| = \left| \begin{array}{cccc} A & O \\ C & B \end{array}\right| = \left| A \right|\left| B \right|$
$\left| \begin{array}{cccc} O & A \\ B & O \end{array}\right| = \left| \begin{array}{cccc} C & A \\ B & O \end{array}\right| = \left| \begin{array}{cccc} O & A \\ B & C \end{array}\right| = (-1)^{mn}\left| A \right|\left| B \right|$
范德蒙德行列式
$\left|\begin{array}{cccc} 1&1&\cdots&1\\ x_1&x_2&\cdots&x_n\\ x_1^2&x_2^2&\cdots&x_n^2\\ \vdots&\vdots&&\vdots\\ x_1^{n-1}&x_2^{n-1}&\cdots&x_n^{n-1} \end{array}\right| = \prod_{1\leq i < j \leq n}(x_j-x_i).$