皮尔森相关系数

作用

如衡量国民收入和居民储蓄存款、身高和体重、高中成绩和高考成绩等变量间的线性相关关系。
当两个变量都是正态连续变量，而且两者之间呈线性关系时，表现这两个变量之间相关程度用积差相关系数，主要有Pearson简单相关系数。

表现强度

相关系数的绝对值越大，相关性越强：相关系数越接近于1或-1，相关度越强，
相关系数越接近于0，相关度越弱。
通常情况下通过以下取值范围判断变量的相关强度：
相关系数 0.8-1.0 极强相关
0.6-0.8 强相关
0.4-0.6 中等程度相关
0.2-0.4 弱相关
0.0-0.2 极弱相关或无相关

数学公式:

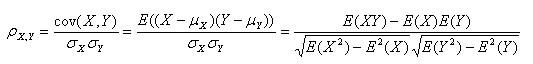
（其中，E为数学期望或均值，N为数据的数目，E{ [X-E(X)] [Y-E(Y)]}称为随机变量X与Y的协方差，记为Cov(X,Y)）

代码：

from scipy.stats import pearsonr
 
m = [0.5, 0.4