线性代数：第二章 矩阵及其运算

本文是马同学高等数学的学习笔记！

第二章 矩阵及其计算

2.1 线性方程组和矩阵

2.1.1 矩阵

矩阵的定义 :
由 $m\times n$个数$a_{ij}(i=1,2,\cdots m;j=1,2,\cdots n)$排成的m行n列的数表称为m行n列矩阵，简称$m\times n$矩阵，记作：
$$A=\left(\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ \cdots & \cdots & & \cdots \\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right)$$
这$m\times n$个数称为矩阵$A$的元素。

矩阵简写 ：
数$a_{i,j}$表示矩阵$A$的第$i$行$j$列的数，称为矩阵$A$的$(i,j)$元。
以数$a_{i,j}$为$(i,j)$元的矩阵记作$(a_{ij})$。
$m\times n$矩阵$A$也记作$A_{m\times n}$。

行矩阵与列矩阵 ：
行数与列数都等于n的矩阵称为n阶矩阵或者n阶方阵。
只有一行的矩阵：
$$A=\left(\begin{array}{c}{a}_1,a_2,\cdots a_n\end{array}\right)$$
称为行矩阵，又称行向量。
只有一列的矩阵：
$$B=\left(\begin{array}{c}{b}_1\\ b_2\\ ⋮\\ b_m\end{array}\right)$$
称为列矩阵，又称列向量。

2.2 高斯消元法与阶梯矩阵

2.2.1 单位阵

若n阶方阵从左上角到右下角的直线(对角线)以外的元素都是0，这种方阵称为对角矩阵，简称对角阵，也记作：
$$A=diag({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n)$$
特别地，当均为1时，对应的方阵称为n阶单位矩阵(identity matrix)

注：若$AB=B$，则$A$也不一定为单位矩阵。
如：
$$\left(\begin{array}{cc}\frac{1}{3}& \frac{1}{3}\\ 0& 1\end{array}\right)\left(\begin{array}{cc}1& 1\\ 2& 2\end{array}\right)=\left(\begin{array}{cc}1& 1\\ 2& 2\end{array}\right)$$

2.2.2 初等变换与初等矩阵

Guass消元法只需要三种操作就可以实现，这三种操作对应了三种矩阵：

名称	操作	应用到单位阵
倍加变换	$r_1^{{}^{\prime }}=r_1+k{r}_2$	$\left(\begin{array}{ccc}1& k& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)$
倍乘变换	$r_1^{{}^{\prime }}=k{r}_1(k̸=0)$	$\left(\begin{array}{ccc}k& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)$
对换变换	$r_1\leftrightarrow r_2$	$\left(\begin{array}{ccc}0& 1& 0\\ 1& 0& 0\\ 0& 0& 1\end{array}\right)$

以上三种称为初等行变换,初等行变换和初等列变换合称初等变换。
把对单位阵实施一次初等变换得到的矩阵称为:初等矩阵

2.2.3 阶梯矩阵

非零矩阵若满足：

• 非零行在零行的上面
• 某一行的先导元素所在的列位于前一行先导元素的右边
• 某一先导元素所在列的下方元素都是0

则称此矩阵为行阶梯矩阵，阶梯矩阵中的非零行的先导元素称为主元。
其中先导元素指的是非零行中最左边的非零元素。

若$A$是行阶梯矩阵，并且还满足：

• 非零行的先导元素为1
• 先导元素所在的列的其他元素均为0

则称$A$为行最简矩阵

2.3 矩阵运算(上)–加法和乘法

2.3.1 同型矩阵与矩阵相等

同型矩阵 ： 两个矩阵的行数和列数相等。

矩阵相等 ： 如果$A$ 与 $B$ 是同型矩阵，且它们的对应元素相等，则矩阵$A$和矩阵$B$相等，记作：$A=B$。

零矩阵 : 元素都是零的矩阵称为零矩阵，记作$O$，注意不同型的零矩阵是不同的。

2.3.2 矩阵加法与数乘

加法定义 ：设有两个$m\times n$矩阵 $A=(a_{ij})$和$B=(b_{ij})$，那么矩阵$A$和$B$的和记为$A+B$，规定为：
$$A+B=\left(\begin{array}{cccc}{a}_{11}+b_{11}& a_{12}+b_{12}& \cdots & a_{1n}+b_{1n}\\ a_{21}+b_{21}& a_{22}+b_{22}& \cdots & a_{2n}+b_{2n}\\ \cdots & \cdots & & \cdots \\ a_{m1}+b_{m1}& a_{m2}+b_{m2}& \cdots & a_{mn}+b_{mn}\end{array}\right)$$

$-A$称为矩阵$A$的负矩阵，记作：
$$-A=(-a_{ij})$$
显然有：
$$A+(-A)=O$$

数乘定义 ： 数$k$与矩阵$A$的乘积记作：
$$kA或Ak$$
规定为：
$$kA=Ak=\left(\begin{array}{cccc}k{a}_{11}& k{a}_{12}& \cdots & k{a}_{1n}\\ k{a}_{21}& k{a}_{22}& \cdots & k{a}_{2n}\\ \cdots & \cdots & & \cdots \\ k{a}_{m1}& k{a}_{m2}& \cdots & k{a}_{mn}\end{array}\right)$$

2.3.3 矩阵乘法的合法性

• $m\times n$的矩阵只能和$n\times p$矩阵相乘
• 相乘后的矩阵大小为 $m\times p$

2.3.4 行观点、列观点与点积观点

行观点 :
假设：
$x=(x_1,x_2,\cdots ,x_m),A=\left(\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ \cdots & \cdots & & \cdots \\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right)$
计算$xA$，将结果看成行向量的线性组合：
$$xA=(x_1,x_2,\cdots ,x_m)\left(\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ \cdots & \cdots & & \cdots \\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right)=x_1(a_{11},a_{12},\cdots ,a_{1n})+\cdots +x_m(a_{m1},\cdots ,a_{mn})$$
此时$A$在行向量$x$的右边，可以说$A$右乘x。

列观点 ：
假设：
$x=\left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right),A=\left(\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ \cdots & \cdots & & \cdots \\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right)$
计算$Ax$,将结果看成列向量的线性组合:
$$Ax=\left(\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ \cdots & \cdots & & \cdots \\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right)=x_1\left(\begin{array}{c}{a}_{11}\\ a_{21}\\ ⋮\\ a_{m1}\end{array}\right)+x_2\left(\begin{array}{c}{a}_{12}\\ a_{22}\\ ⋮\\ a_{m2}\end{array}\right)+\cdots +x_n\left(\begin{array}{c}{a}_{1n}\\ a_{2n}\\ ⋮\\ a_{mn}\end{array}\right)$$
此时，A在列向量$x$的左边，可以说$A$左乘$x$。

点积观点 ：
设$A=(a_{ij})$是$m\times s$矩阵， $B=(b_{ij})$是一个$s\times n$矩阵，那么规定矩阵$A$与$B$的乘积是一个$m\times n$的矩阵$C=(c_{ij})$，其中：
$$c_{ij}=\sum _{k=1}^s{a}_{ik}{b}_{kj}$$，记作：
$$C=AB$$

2.4 矩阵运算(下)–幂运算与转置

2.4.1 矩阵的幂

设$A$是n阶方阵，定义：
$$A^1=A,A^2=A^1{A}^1,\cdots ,A^{k+1}=A^k{A}^1$$
其中$k$为正整数，也就是说，$A^k$就是$k$个$A$连乘。只有方阵的幂才有意义。

2.4.2 矩阵的转置

将矩阵$A$的行换成同序数的列得到一个新矩阵，叫做$A$的转置矩阵,记作：
$$A^T$$
则行向量和列向量互为转置矩阵。
而向量默认为列向量，则行向量用列向量的转置来表达。
$$x=\left(\begin{array}{c}{a}_1\\ a_2\\ ⋮\\ a_n\end{array}\right),x^T=(a_1,a_2,\cdots ,a_n)$$

2.4.3 转置矩阵的性质

$$(AB{)}^T=B^T{A}^T$$
特殊的转置矩阵：
若：
$$A^T=A$$则矩阵$A$称为对称矩阵。
若：
$$A^T=-A$$则矩阵$A$称为反对称矩阵。

2.5 矩阵乘法是线性函数

2.5.1 线性函数的定义

满足以下条件的函数是线性函数：

• 齐次性： $L(mx)=mL(x)$
• 可加性： $L(x+y)=L(x)+L(y)$

齐次性 ： 输入是m倍、输出也是m倍。

2.5.2 矩阵函数是线性函数

$$A(mx)=m(Ax)$$
$$A(x+y)=A(x)+A(y)$$

2.5.3 一点补充

对一般函数$f(x)$而言，存在$f(x)=b$只有一个解，而$f(x)=c$有多个解的情况。
如： $f(x)=x^2$

• $x^2=0$有一个解
• $x^2=4$有两个解
  然而线性函数不存在这样的情况。

命题 ：
设$Ax$是线性函数，且$Ax=b$有多个不同解，则若$Ax=c$有解，一定也是多个不同解。
proof:
设$x_1$是$Ax=c$的一个解。$x_2、x_3$是$Ax=b$的两个不同解。
由线性函数的可加性：
$$A(x_1+(x_2-x_3))=A{x}_1+A{x}_2-A{x}_3=c+b-b=c$$
说明$x_1+x_2-x_3$也是$Ax=c$的解。
即$Ax=c$也有多个不同解。

2.6 矩阵乘法的几何意义

2.6.1 坐标

给向量空间加上坐标系——自然基。(一般情况下，向量空间默认选择自然基作为基)

$$i=\left(\begin{array}{c}1\\ 0\end{array}\right),j=\left(\begin{array}{c}0\\ 1\end{array}\right)$$

令：$$A=\left(\begin{array}{cc}1& -1\\ 1& 1\end{array}\right)$$
再选取：
$$a=\left(\begin{array}{c}1\\ 1\end{array}\right)=1i+1j$$
根据矩阵乘法的规则，$Aa=b$计算如下：
$$Aa=\left(\begin{array}{cc}1& -1\\ 1& 1\end{array}\right)\left(\begin{array}{c}1\\ 1\end{array}\right)=1\left(\begin{array}{c}1\\ 1\end{array}\right)+1\left(\begin{array}{c}-1\\ 1\end{array}\right)=\left(\begin{array}{c}0\\ 2\end{array}\right)=b$$

这个过程可以看作矩阵列向量的线性组合。
令：
$$c_1=\left(\begin{array}{c}1\\ 1\end{array}\right),c_2=\left(\begin{array}{c}-1\\ 1\end{array}\right)$$
则：
$$a=1i+1j\stackrel{A}{⟶}b=1c_1+1c_2$$
也就是保持系数不变，但是自然基被矩阵的列向量给替换了。

2.6.2 旋转矩阵

单位圆中，与$x$轴夹角为$\alpha$的向量表示如下：

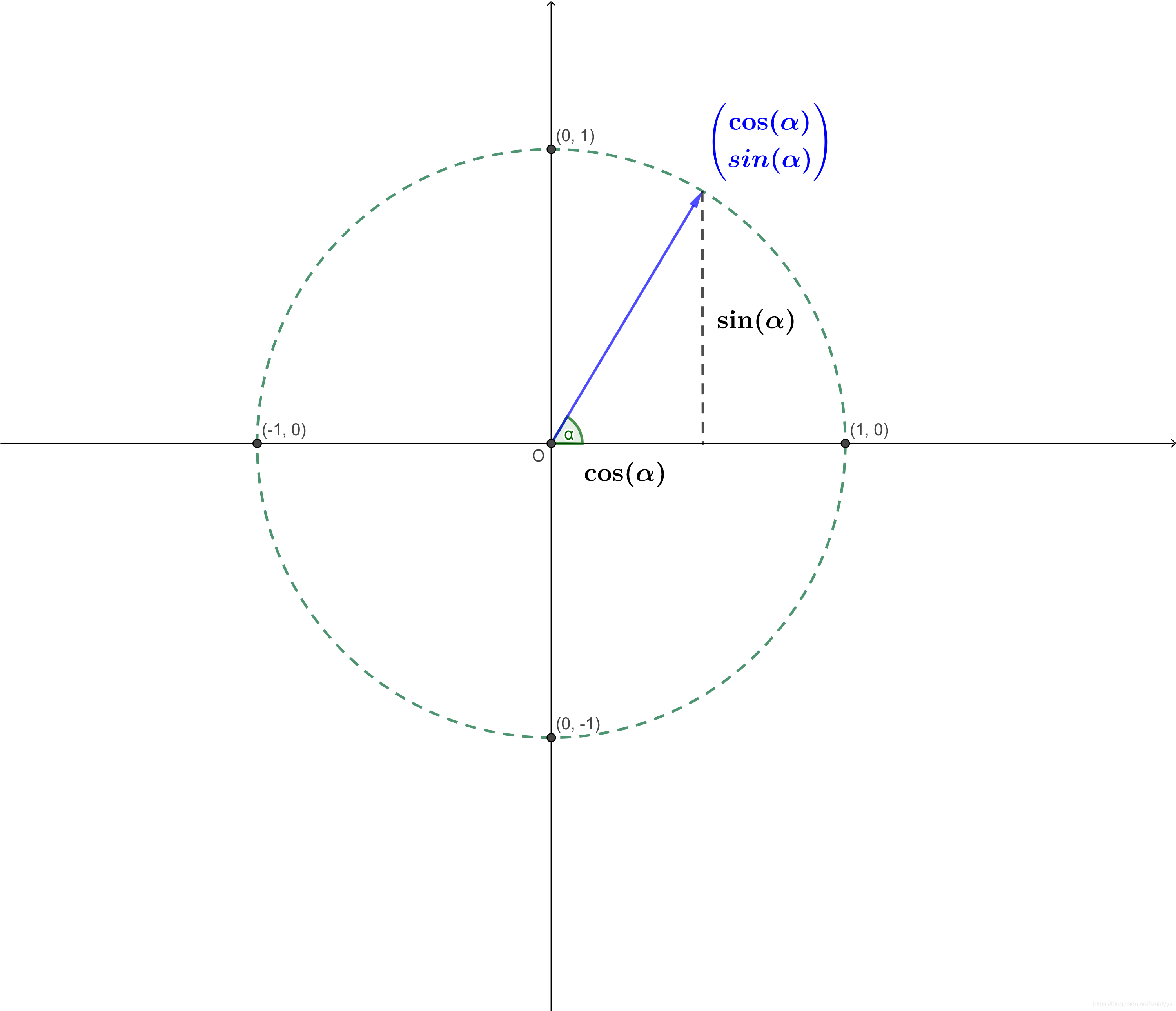
则：

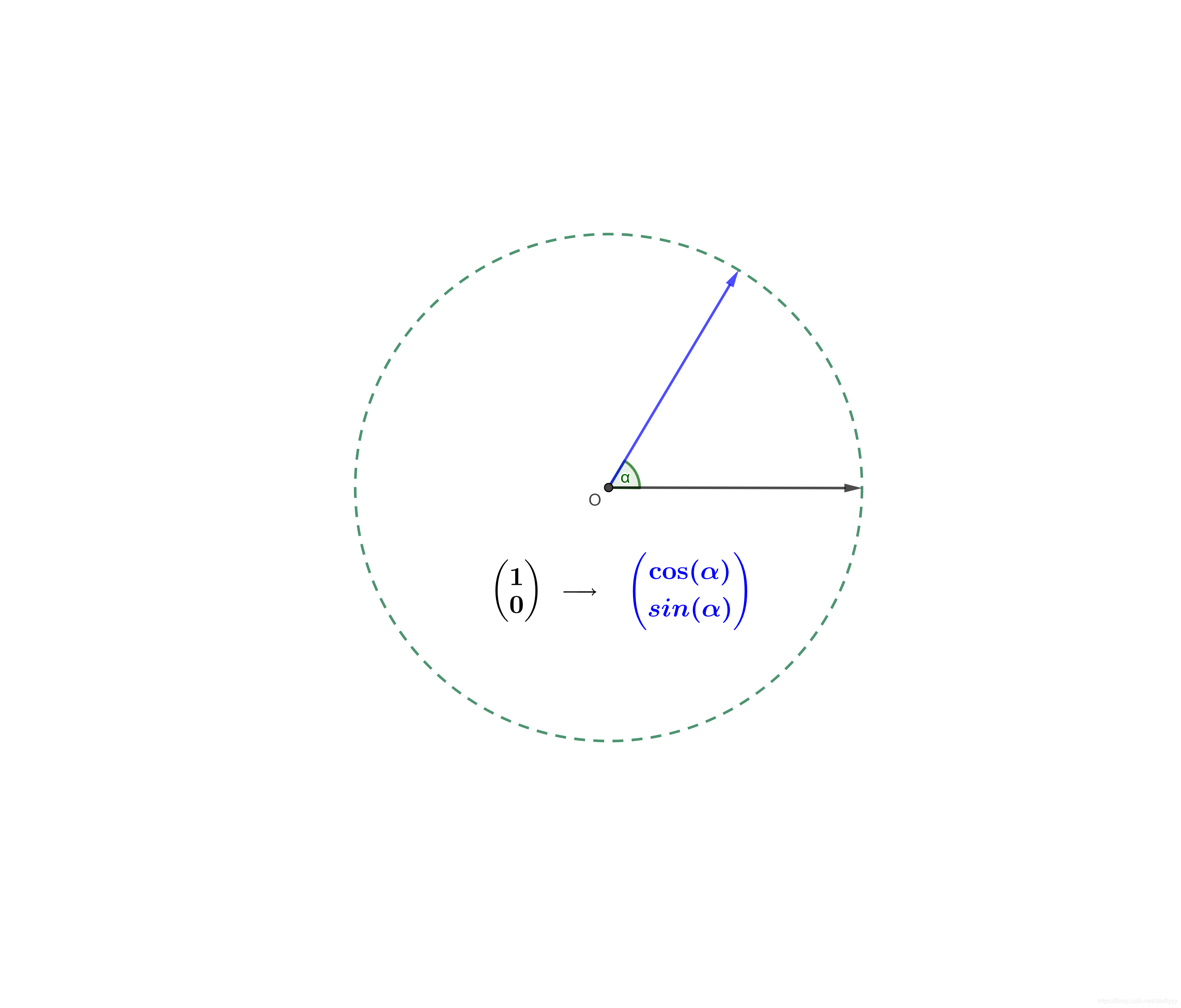
与$y$轴夹角为$\alpha$的向量表示如下：

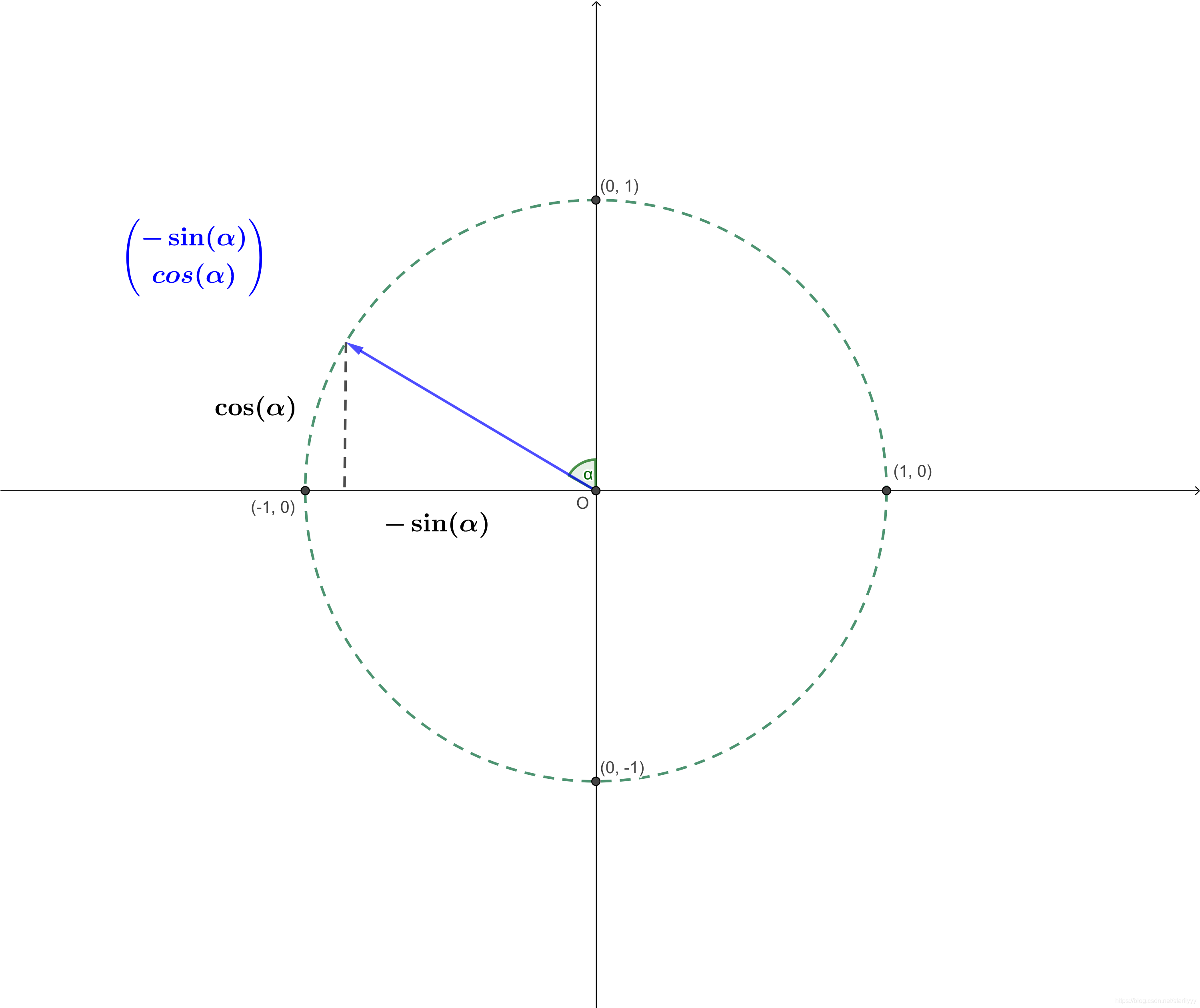
则：

$$x_{1}i+x_{2}j\stackrel{A=\left(\begin{array}{cc}\cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array}\right)}{⟶}{x}_1\left(\begin{array}{c}\cos \alpha \\ \sin \alpha \end{array}\right)+x_2\left(\begin{array}{c}-\sin \alpha \\ \cos \alpha \end{array}\right)$$

旋转矩阵的原理，就是通过旋转基来实现的。

2.7 基本矩阵及矩阵函数的性质

2.7.1 向量函数的图像

矩阵函数是一个向量函数，它的作用需要比较两个向量空间中的点的变化而得出：

将向量用点来表示，再将各个点连接起来，构成几何图形。如此就可以看出矩形函数的特征。

2.7.2 基本函数图像

$R^2\to R^2$基本矩阵

• 单位矩阵
  什么都不改变的矩阵称作单位矩阵：
  

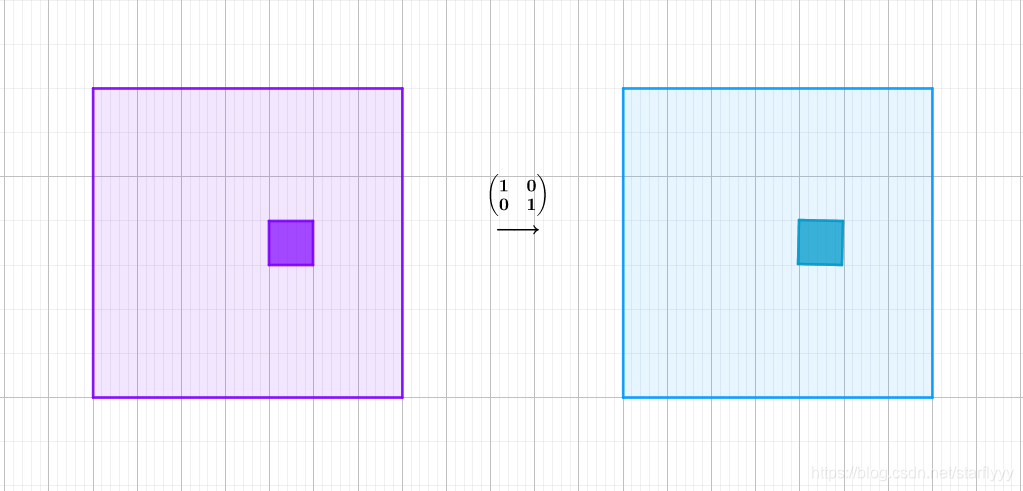
• 伸缩矩阵
  在某个基(或每个基)方向上进行了缩放。
  选取$i,j$为基，下图是在$j$方向上伸长了c倍：
  

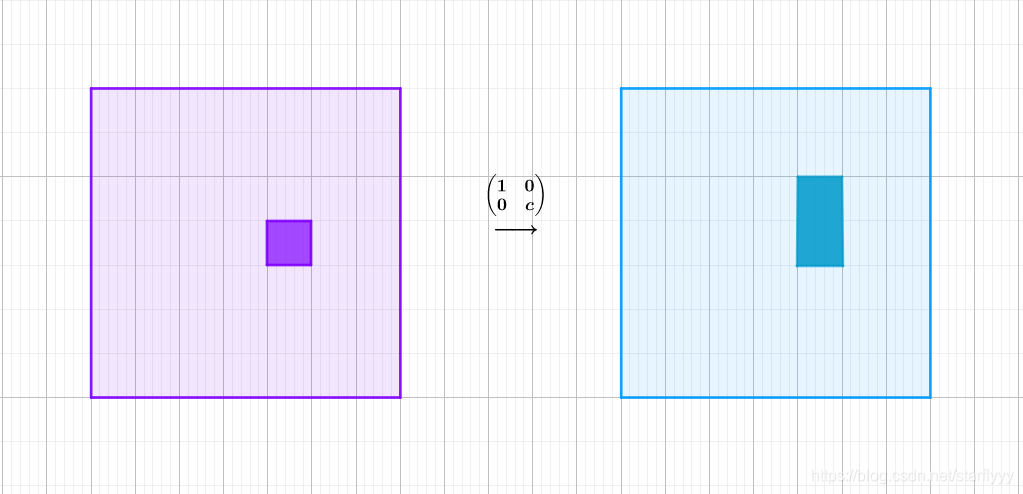
• 旋转矩阵
  围绕原点，几何图形进行了旋转。下图是沿逆时针旋转了$\theta$角:
  

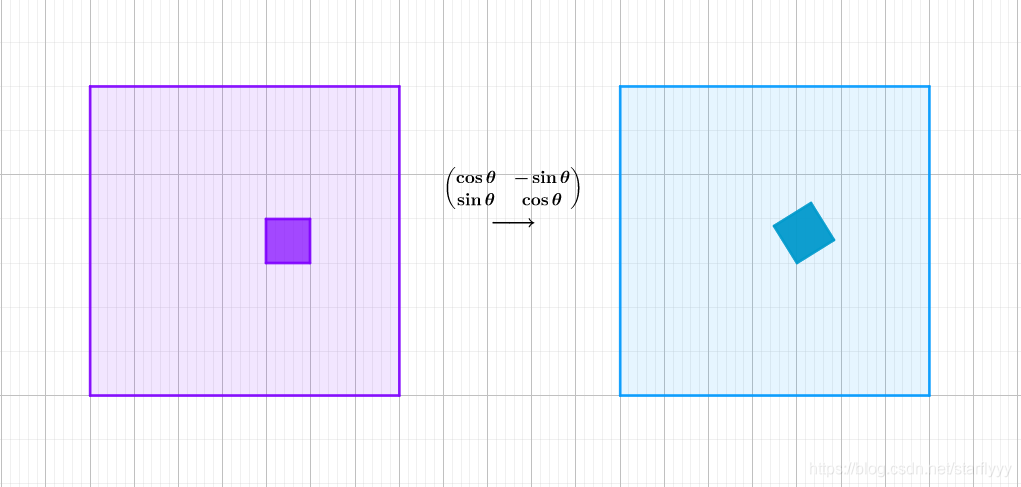
• 剪切矩阵
  是通过在某个基上平移$c$，将正方形变换成一般的平行四边形。
  选取$i,j$为基，下图是在i方向平移了$c$:
  

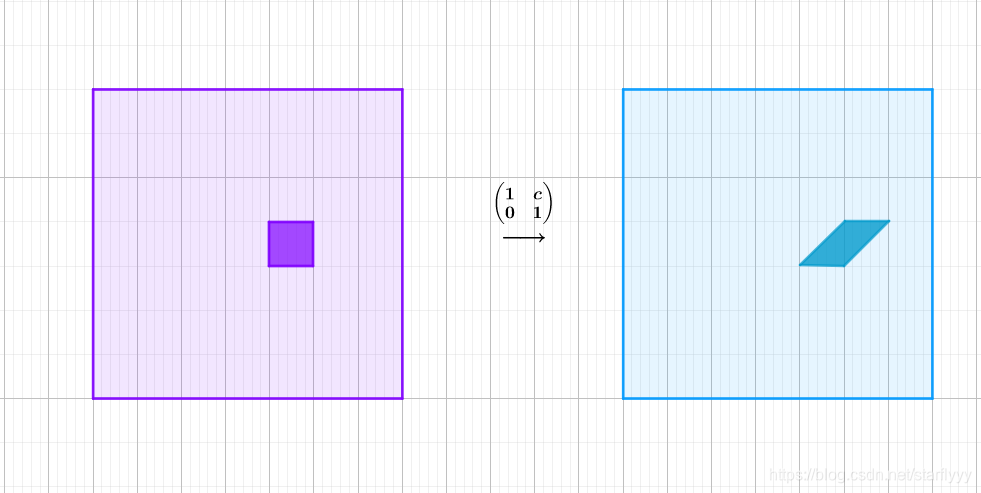
• 镜像矩阵
  将平面上任一点$(x,y)$变换成$(y,x)$，可以理解为以$y=x$为对称轴的"镜射"：
  

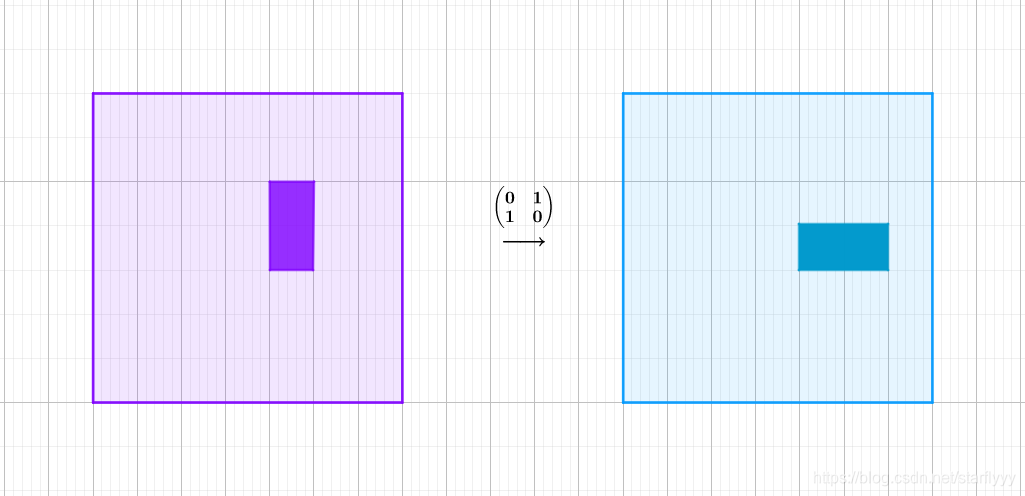
2.7.3 交换律、结合律和分配律

矩阵乘法作为线性函数，首先不满足交换律。
从复合函数的角度来看，复合的主次很重要。
对于矩阵乘法而言：

• 一般来说：$$AB̸=BA$$
• $BA=O$不一定有$B=O$或$A=O$

复合函数中，在主次不变的前提下，复合的顺序不重要，矩阵的乘法满足结合律。
$$(AB)C=A(BC)$$

分配律即可加性：
$$A(B+C)=AB+AC$$