地震数据处理研究（Matlab代码实现）

 👨‍🎓个人主页

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

1. 峰值地面加速度（PGA）

2. 峰值地速（PGV）

3. 峰值地面位移（PGD）

4. 总累积能量与归一化累积能量-时间关系

5. Trifunac & Brady（1975）D_5_95重要持续时间

6. 持续时间D_5_75

7. 总咏叹调强度（Ia）

8. 速度时程基线校正

9. 位移时间历史基线校正

10. 重采样加速度时间历史

11-15. 线弹性反应谱

16-18. 恒定延性反应谱

19. 傅里叶振幅谱

20. 平均周期（Tm）

21-22. 巴特沃斯滤波

23. SDOF增量动态分析（IDA）

总结

📚2 运行结果

🎉3 参考文献

 🌈4 Matlab代码实现

---

💥1 概述

1. 峰值地面加速度（PGA）

PGA定义为地震加速度时间历程中绝对值的最大值，计算公式为 PGA=max⁡t∈T∣a(t)∣，直接反映地震动对结构的瞬时冲击强度。其工程意义在于评估地震对短周期结构的破坏潜力。例如，汶川地震中成都市区的PGA达到0.25g，导致大量建筑损毁。

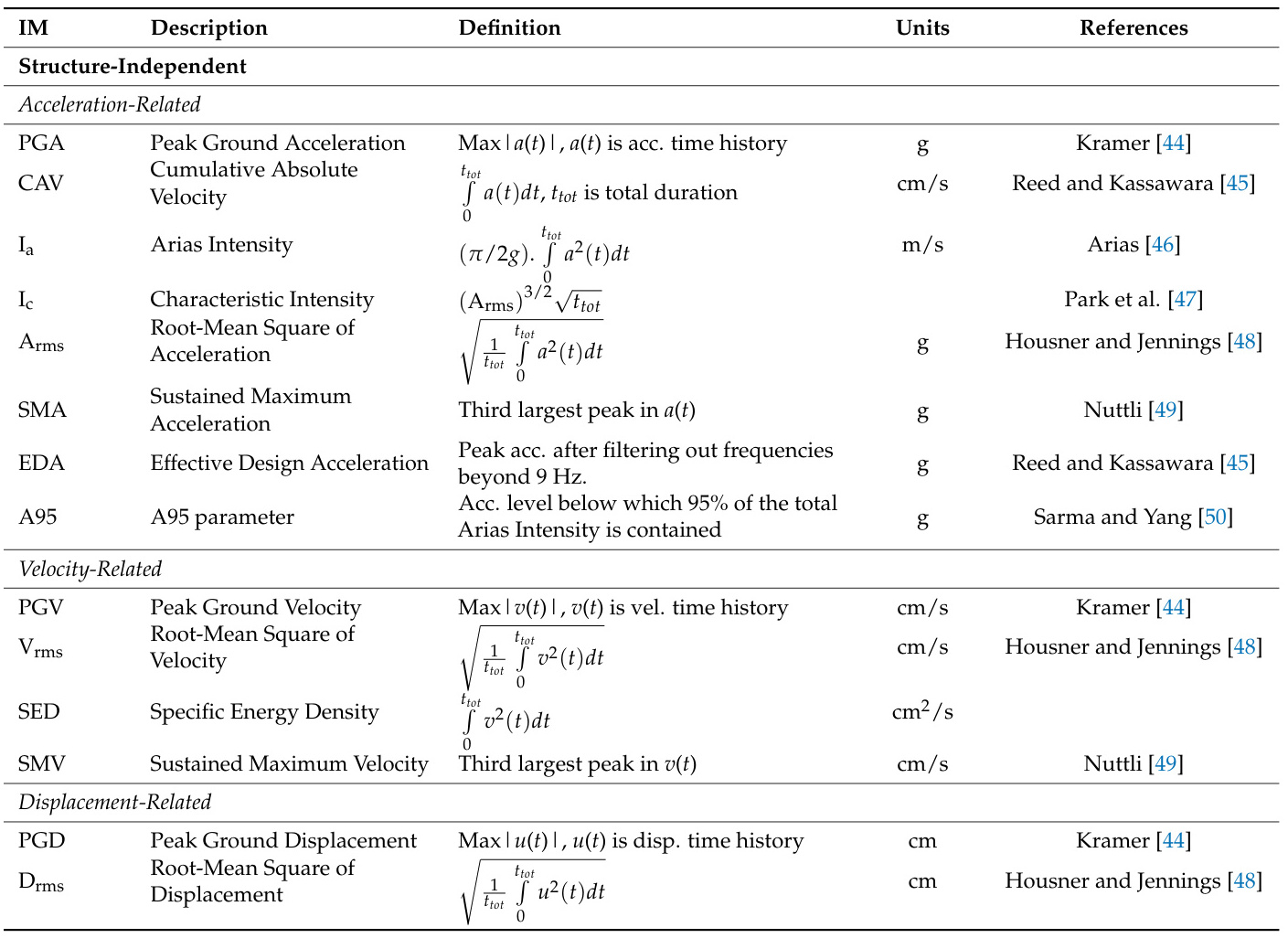
2. 峰值地速（PGV）

PGV是速度时间历程的最大绝对值，计算需对加速度积分：损伤相关性更强。Newmark和Hall提出的经验公式 PGV=PSA(1 s)×37.27×2.54 常用于从谱加速度推导PGV。

3. 峰值地面位移（PGD）

PGD通过双重积分加速度获得位移时间历程的最大绝对值，即 PGD=max⁡t∈T∣d(t)∣PGD=maxt∈T​∣d(t)∣。其重要性在于评估断层滑动、土体液化等长周期效应。例如，GPS观测数据常用于验证基线校正后的位移结果。

---

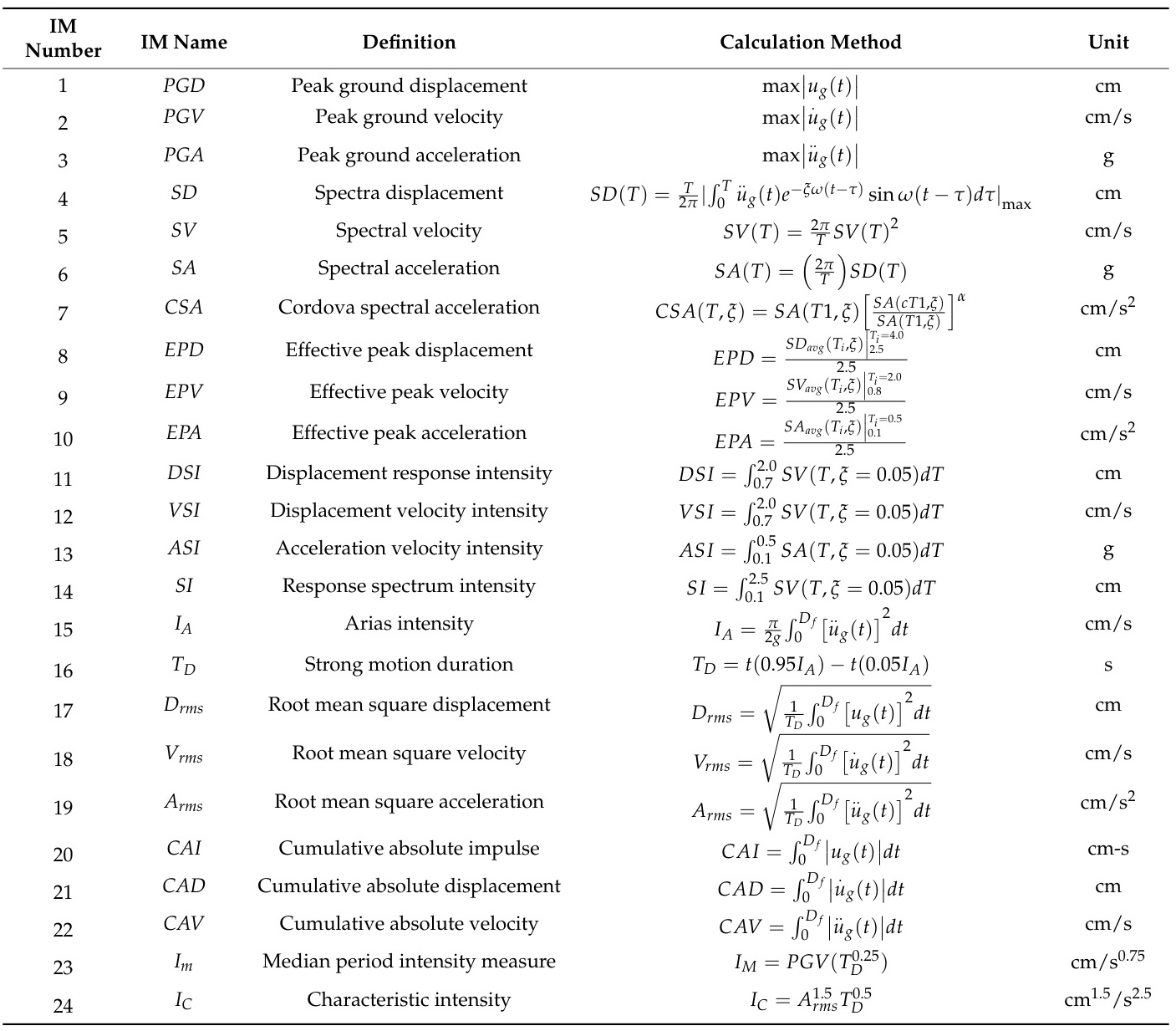
4. 总累积能量与归一化累积能量-时间关系

总累积能量基于Arias强度 Ia=π2g∫0tfa2(t)dtIa​=2gπ​∫0tf​​a2(t)dt，反映地震动总能量输入。归一化累积能量曲线（Husid图）显示能量随时间的累积比例，典型区间为5%-95%（D_5_95持续时间）。显示不同能量等级的归一化曲线形态差异：300 MeV能量在1秒内达到饱和，而100 MeV需要更长时间。

---

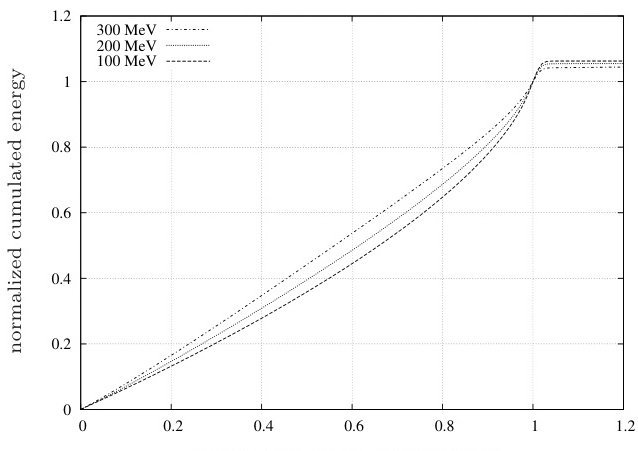
5. Trifunac & Brady（1975）D_5_95重要持续时间

定义：Arias强度累积至总能量5%和95%的时间差。该参数表征地震动的"强震阶段"，与结构累积损伤相关。例如，1989年Loma Prieta地震的Saratoga-Aloha记录显示D_5_95为8.7秒，对应主要能量释放时段。

6. 持续时间D_5_75

类似D_5_95但采用75%能量阈值，更关注能量集中释放阶段。研究表明，D_5_75在20-80秒区间内与CAV（累积绝对速度）呈正相关，适用于评估长持时地震（如俯冲带地震）对非线性结构的疲劳效应。

---

7. 总咏叹调强度（Ia）

器处理低频噪声，提高对高频能量占比的敏感性。例如，九寨沟余震中边坡表面Ia值较坡脚放大5.84倍，揭示地形放大效应。

---

8. 速度时程基线校正

基线漂移会导致积分位移出现虚假趋势。常用方法包括：

• 多项式拟合：用三次多项式拟合速度末尾段，消除线性/非线性偏移。
• 分段校正：结合Iwan方法，选取速度末尾段拟合直线，确定偏移起始点后修正加速度。
• EMD-DNN混合模型：通过经验模态分解与深度学习联合处理大幅值漂移，精度较传统方法提升30%。

9. 位移时间历史基线校正

校正目标为消除二次积分后的基线漂移。SeismoSignal软件采用多项式回归（最高三阶），从加速度中减去拟合曲线。例如，未校正位移可能出现数米级偏移，经线性校正后可恢复真实地壳形变。

---

10. 重采样加速度时间历史

重采样用于统一时间步长或满足数值积分稳定性要求。关键技术包括：

• 线性插值：保持信号能量守恒，适用于步长微调（如从0.01s调整为0.005s）。
• 半时间步长法：当特征频率步长比 ΔtT>0.02TΔt​>0.02 时，自动细分步长以保证谱计算精度。

---

11-15. 线弹性反应谱

• 赝加速度谱：SA=ω2SD​，与基底剪力直接相关，用于弹性设计。
• 赝速度谱：SV=ωSD，表征系统吸收能量，中频段与真实速度谱接近。
• 位移谱：反映长周期分量影响，对隔震结构设计至关重要。
• 速度/加速度谱：分别用绝对加速度和相对速度的最大值生成，适用于不同频段结构分析。

生成流程：对SDOF系统输入地震动，计算各周期对应的最大响应。OpenSeismoMatlab通过自动调整积分步长确保精度，支持阻尼比0-20%。

---

16-18. 恒定延性反应谱

考虑材料非线性，定义目标延性系数μ（如μ=2）。计算时迭代调整强度直至位移延性达到设定值。工程意义：

• 位移谱：评估结构弹塑性变形能力，指导性能化设计。
• 加速度谱：反映非线性阶段的等效惯性力，用于承载力校核。

---

19. 傅里叶振幅谱

通过FFT将时程转换为频域能量分布，识别主导频率。例如，El Centro记录的NS向谱在2.5Hz处出现峰值，与当地场地卓越频率吻合。结合功率谱可计算平均周期Tm。

---

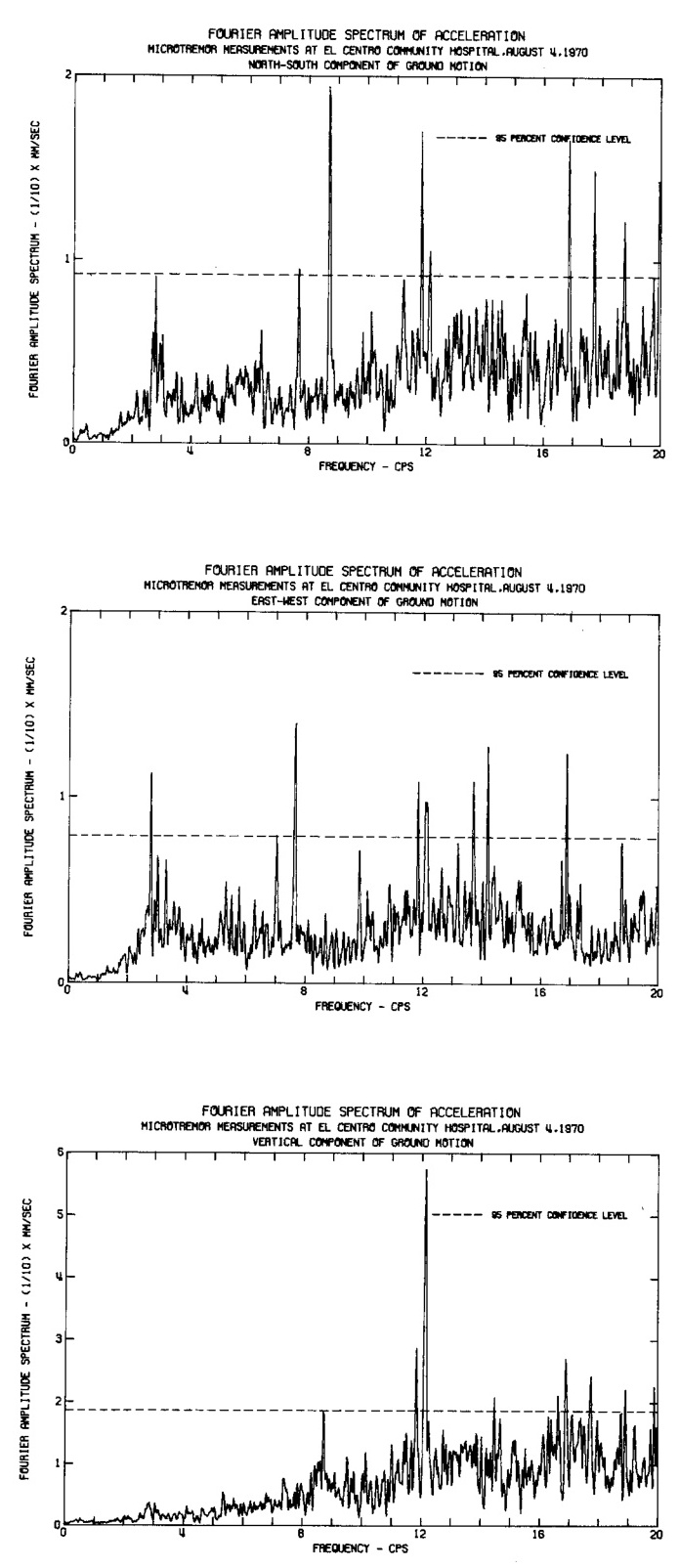
20. 平均周期（Tm）

计算公式：Tm=∑(Ai2/fi)∑Ai2，其中A_i为傅里叶幅值，f_i为频率。Tm反映地震动能量集中频段，用于匹配设计谱。研究显示，传统算法可能低估Tm，推荐功率加权法（Tm6）提高精度。

---

21-22. 巴特沃斯滤波

• 低通滤波：截止频率常设为f_max=25Hz，消除高频噪声。8阶滤波器可实现在350Hz处衰减0.1dB，400Hz衰减50dB。
• 高通滤波：截止频率f_min=0.1Hz，消除基线漂移。需注意相位失真问题，建议采用零相位滤波。

---

23. SDOF增量动态分析（IDA）

实施步骤：

1. 推覆分析：获取基底剪力-位移曲线，等效为SDOF系统。
2. 强度调幅：按比例缩放地震动，逐步增加直至结构倒塌。
3. 损伤评估：记录各强度水平下的层间位移角，建立易损性曲线。

案例：某RC结构在IDA分析中显示，当谱加速度达0.6g时，位移延性μ超过4，对应倒塌概率50%。

---

总结

本文档整合了23项核心地震动参数的定义、计算方法和工程应用，覆盖时域、频域及非线性分析。实际应用中需根据结构特性（如周期、延性）和地震动特征（如持时、能量分布）选择合适的参数组合。例如，短周期建筑关注PGA和加速度谱，桥梁需结合PGV和延性谱，而长周期隔震结构则依赖PGD和位移谱。

📚2 运行结果

 

 

 

部分代码：

%% Earthquake motion
% Load earthquake data
eqmotions={'LomaPrietaHallsValley90'};
data=load([eqmotions{1},'.dat']);
t=data(:,1);
dt=t(2)-t(1);
xgtt=data(:,2);

%% Adjust earthquake motion to have D_5_75=8.3sec
% Switch
sw='arias';
%%
% Apply OpenSeismoMatlab
S1=OpenSeismoMatlab(dt,xgtt,sw);
%%
% Duration D_5_75 of the initially loaded motion
S1.Td_5_75
%% 
% S.Td_5_75 must be roughly near 8.3 sec, as required in Mashayekhi et al. (2020)
% We manipulate the strong shaking part of the motion which corresponds to
% the significant duration so that S.Td_5_75 is increased to the desired
% value (8.3 sec)
id1=find(t==S1.t_5_75(1));
id2=find(t==S1.t_5_75(2));
xgtt(id1:id2)=0.8*xgtt(id1:id2);

%% Calculate duration D_5_75 of adjusted earthquake motion
% Switch
sw='arias';
%%
% Apply OpenSeismoMatlab
S2=OpenSeismoMatlab(dt,xgtt,sw);
%%
% Duration D_5_75 of the adjusted motion
S2.Td_5_75

%% Scale earthquake motion to have Sa(1 sec)=0.382g
% Switch
sw='es';
%%
% Critical damping ratio
ksi=0.05;
%%
% Period where Sa=0.382g
T=1;
%%
% Apply OpenSeismoMatlab
S3=OpenSeismoMatlab(dt,xgtt,sw,T,ksi);
%%
% Spectral acceleration of the adjusted motion at 1 sec
S3.Sa
%%
% Sa at 1 sec must be equal to 0.382g, so we scale the entire acceleration
% time history up to this level
scaleF=0.382*9.81/S3.Sa;
xgtt=xgtt*scaleF;

%% Calculate spectral acceleration of scaled earthquake motion
% Switch
sw='es';
%%
% Critical damping ratio
ksi=0.05;
%%
% Period where Sa=0.382g
T=1;
%%
% Apply OpenSeismoMatlab
S4=OpenSeismoMatlab(dt,xgtt,sw,T,ksi);
%%
% Spectral acceleration of the adjusted motion at 1 sec
S4.Sa

%% Plot the acceleration time history

% Initialize figure
figure()
% Plot the acceleration time history of the adjusted motion
plot(t,xgtt)
% Finalize figure
grid on
xlabel('Time (sec)')
ylabel('Acceleration (g)')

%% Perform IDA analysis
% Switch
sw='ida';
%%
% Eigenperiod
T=1;
%%
% Scaling factors
lambdaF=logspace(log10(0.001),log10(10),100);
%%
% Type of IDA analysis
IM_DM='Sa_disp';
%%
% Mass
m=1;
%%
% Yield displacement
uy = 0.082*9.81/(2*pi/T)^2;
%%
% Post yield stiffness factor
pysf=0.01;

🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。

 🌈4 Matlab代码实现