【Copula】考虑风光联合出力和相关性的Copula场景生成（Matlab代码实现）

ssswww56

于 2025-04-13 09:03:23 发布

阅读量583

点赞数 18

文章标签： matlab 开发语言

本文链接：https://blog.youkuaiyun.com/ssswww56/article/details/147187161

版权

👨‍🎓个人主页

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

一、Copula基本概念与数学基础

二、风光联合出力的相关性分析与Copula模型选择

三、数据获取与预处理方法

四、基于Copula的场景生成与削减技术

五、评估指标与验证方法

六、实际应用案例

七、结论与展望

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

参考文献：

风光等可再生能源出力的不确定性和相关性给系统的设计带来了极大的复杂性，若忽略这些因

素，势必会在系统规划阶段引入次优决策风险[24]。因此，在确定系统最佳配置方案时，必须要考虑风光出力的不确定性和相关性。 Copula 函数可以描述随机变量间的相关性，是把随机变量的联合分布函数与各自的边缘分布函数相连接的函数。其主要包括椭圆分布族 Copula函数(Normal-Copula、t-Copula)和阿基米德分布族Copula 函数 [25](Frank-Copula 、 Gumbel-Copula 、Clayton-Copula)。Copula 函数的选取对刻画风光出力的相关性至关重要，然而选择何种 Copula 函数取决于规划区域的风光出力特性。由于 t-Copula 对多维随机变量拟合极为耗时且 Gumbel-Copula 形式复杂，因此本文仅考虑其余 3 种 Copula 函数。

为了选择最佳的 Copula 函数拟合风光出力特性，引入 Spearman 秩相关系数[26]、Kendall 秩相关系数及欧式距离等指标并计算风光出力的 Empirical (经验)-Copula 函数[27]，具体详见文献[26-27]。所选Copula 函数的秩相关系数越接近 Empirical-Copula函数的秩相关系数，且与其欧式距离较小者认为是最佳的。本文选取规划区 2011 年全年风机与光伏标幺化出力数据，见附录 A 图 A1，分别用 Normal Copula、Frank-Copula、Clayton-Copula 函数拟合风光出力并计算风光出力的 Empirical-Copula 函数，求得其秩相关系数及与 Empirical-Copula 函数的欧式距离如表 1 所示。

Sklar在1959年提出的Sklar定理指出，一个N维分量的联合分布函数可以由这N个变量的边缘分布和1个 Copula函数来描述［11］，即Copula函数可以将多变量的联合分布与这N个变量的边缘分布连接起来，因此也称为“连接函数”。Sklar定理表达式如下：

Sklar定理证明了Copula函数的存在性，描述了多元联合分布密度函数与Copula密度函数的关系，为建模奠定了基础。

Copula函数主要分为椭圆函数族（Ellipse-Copula）和阿基米德函数族（Archimedean-Copula）2种类型。其中，椭圆函数族包括正态Copula函数和t-Copula函数，阿基米德函数族中常用的有Gumbel-Copula函数、Clayton-Copula函数和Frank-Copula函数［12］。不同类型的Copula函数具有不同的函数结构，因其尾部特征的差异适用于刻画不同类型的相依关系，具体特性如表1 所示。

来源：

上节所述5种Copula函数适用于描述具有尖峰厚尾特性的数据，首先对风电场数据进行分析，统计同一地区2个典型风电场1个月的数据，分布特性如图1所示。图1中横坐标代表出力标幺值，纵坐标代表概率密度。由图1可知，风电场输出功率统计数据也具有尖峰厚尾的特性，即大量数据集中在某一区间，频数特别高，而其他数据广泛分布于各个区间，范围广。因此Copula函数及建模方法适用于风电场出力数据。为了对同一地区2个风电场联合出力及相关性有一个直观的认识，便于分析，作2个风电场的联合分布统计图，如图2所示。

由图2可知，大量数据集中在主对角线上，同一地区2个风电场出力呈现出很强的正相关性，依据这种相关特性建立Copula模型可以有效描述同一地区2个风电场的出力特性及其相关性。

一、Copula基本概念与数学基础

Copula是一种连接多维随机变量联合分布与边缘分布的函数，其核心在于将变量的边缘分布与依赖结构解耦，从而灵活建模复杂相关性。

定义与性质：
- Copula是定义在单位超立方体上的联合累积分布函数，满足均匀边缘分布。对于d维随机向量，Copula函数满足：当任意一个变量趋近于0时，Copula值为0；当其他变量均为1时，Copula等于该变量的边缘分布值。
- Sklar定理：任何联合分布函数均可分解为边缘分布和Copula函数的组合，即

$F(x_1, x_2, \dots, x_n) = C(F_1(x_1), F_2(x_2), \dots, F_n(x_n)),$

2. 常见Copula类型：

椭圆族Copula（如高斯Copula、t-Copula）：适用于对称相关结构，但对尾部依赖性建模能力有限。
阿基米德族Copula：如Clayton（下尾相关）、Gumbel（上尾相关）、Frank（对称无尾部相关），能灵活捕捉非对称依赖。
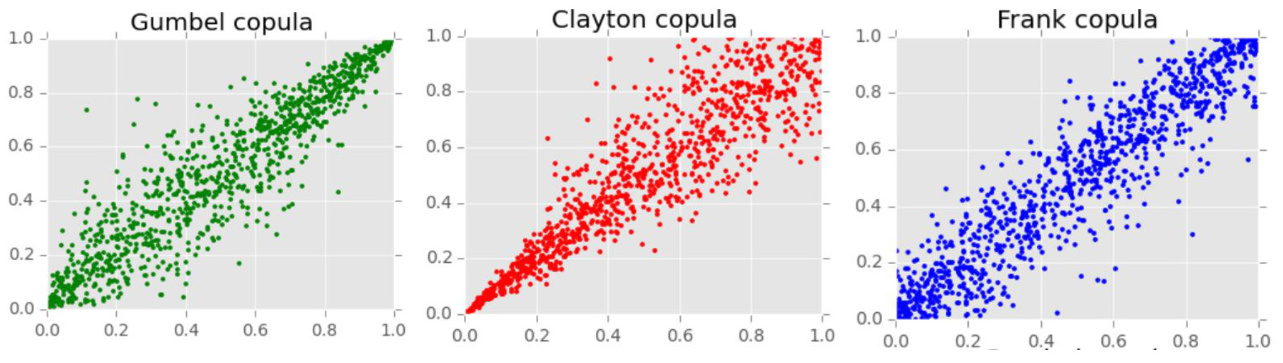
图1展示了不同Copula的二维分布特性，例如Gumbel Copula在高值区聚集，Clayton在低值区集中，而Frank Copula分布均匀[[4]-[8]]。

二、风光联合出力的相关性分析与Copula模型选择

风光出力受气象因素影响，具有时空相关性和非线性依赖特征，Copula可有效建模其联合概率分布。

动态相关性建模：
- 静态Copula（如正态Copula）假设相关性恒定，而实际风光出力相关性随时间变化。动态Copula（如时变参数模型）通过引入动态相关系数（如时变Kendall秩相关系数）提升建模精度。
- 例如，段偲默等通过动态Copula构建8组风光联合出力模型，验证其拟合优度优于静态模型。
Copula选择与验证：
- 拟合优度检验：采用AIC/BIC准则、K-S检验或经验Copula距离（如Cramér-von Mises统计量）评估模型。AIC/BIC值越小，模型越优[[58]-[63]]。
- 尾部依赖性分析：通过尾部相关系数（如Gumbel Copula的λupperλupper）判断风光出力极端事件的相关性。

三、数据获取与预处理方法

数据来源：
- 实测数据：如ISO New England网站的风光出力历史数据。
- 标准化采集：需包含装机容量、地理位置信息，符合GB/T 33604-2017标准。
预处理步骤：
- 非参数核密度估计：估计风光出力的边缘分布，避免参数分布假设偏差。
- 数据清洗：处理缺失值、异常值，并通过小波变换或EMD分解去除随机噪声。
- 归一化与向量化：将出力数据转换为[0,1]区间，便于Copula建模。

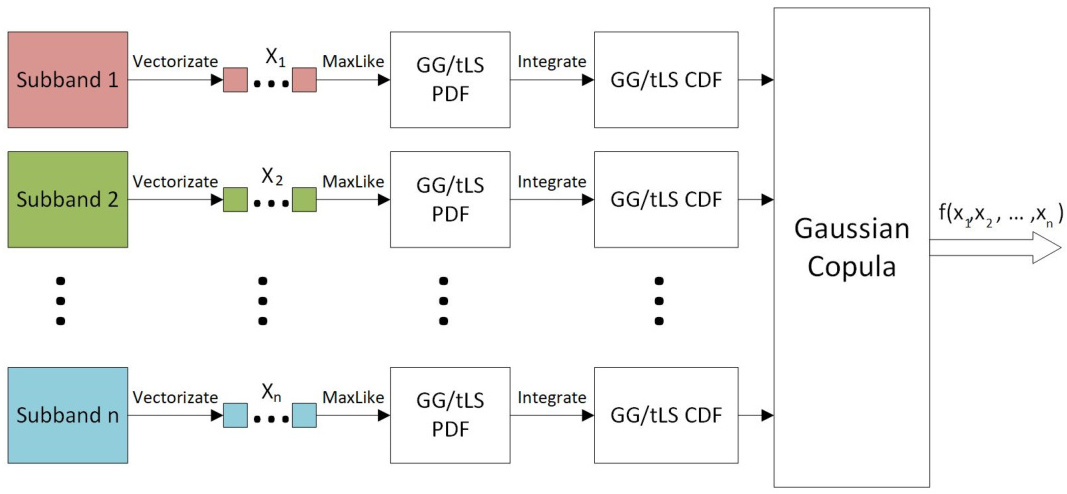
四、基于Copula的场景生成与削减技术

联合分布构建：
- 步骤：
  1. 估计风电、光伏的边缘分布（核密度或参数法）。
  2. 选择Copula类型并参数估计（最大似然法或矩估计）。
  3. 生成服从联合分布的随机样本。
- 案例：使用Frank Copula生成考虑空间相关性的风光场景，并通过K-means聚类将场景削减至5个典型场景，保留概率信息。
场景削减优化：
- K-means聚类：基于欧氏距离或概率距离（如Wasserstein距离）合并相似场景，降低计算复杂度。
- 同步反向削减法：结合场景树技术，保留反映风光出力波动特性的关键场景。

五、评估指标与验证方法

统计指标：
- 能量分数（ES） ：衡量生成场景与实际数据的分布差异，ES值越小越好。
- 自相关函数（ACF）与交叉相关函数（CCF） ：验证时间序列波动特性和空间相关性。
模型性能验证：
- 可靠性指数与尖锐度指数：评估概率区间的覆盖能力和冗余度。
- 对比实验：与传统蒙特卡洛或拉丁超立方方法比较，验证Copula在相关性建模上的优势。