【电动车】基于削峰填谷的电动汽车多目标优化调度策略研究（Matlab代码实现）

ssswww56

于 2025-04-13 08:57:51 发布

阅读量588

点赞数 25

文章标签： matlab 开发语言

本文链接：https://blog.youkuaiyun.com/ssswww56/article/details/147187060

版权

👨‍🎓个人主页

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

1.1 综合负荷成本以及电动汽车电池退化损耗成本

1.2 削峰填谷的峰谷差最低

1.3 负荷波动最低

基于削峰填谷的电动汽车多目标优化调度策略研究

一、削峰填谷技术的基本原理与电力系统需求

二、电动汽车作为可调度负荷的特性分析

三、多目标优化调度策略的核心要素与目标函数

四、电动汽车与削峰填谷的协同效应

五、典型多目标优化算法在调度中的应用

六、充电负荷预测模型与数据需求

七、电网侧与用户侧利益平衡机制设计

八、未来研究方向与挑战

总结

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、文章讲解

💥1 概述

大量电动汽车投入运营，将对电力系统产生很大影响。电动汽车充放电机产生的谐波将恶化局部电网的电能质量; 同时，电动汽车充放电在时间和空间上具有一定的随机性和间歇性。在非低谷用电期的充电行为将拉高负荷峰值，当现有配电网线路容量裕度较小时会使系统过载。同样，对电动汽车放电不加控制也很难使其起到削峰的作用。因此，建立一个电动汽车充放电控制策略，从整体上协调区域内电动汽车的充放电，能够在很大程度上消除电动汽车充放电随机性对电网造成的不利影响，对于提高电动汽车规模化应用后电网的安全性具有重大的现实意义。

本文考虑电动汽车参与削峰填谷的场景下，电动汽车充放电策略的优化，本文目标函数有三个：

1 电动汽车综合负荷以及电池退化损耗成本

2 削峰填谷的峰谷差最低

3 负荷波动最低

1.1 综合负荷成本以及电动汽车电池退化损耗成本

$\begin{array}{c} F_{1}=\min \sum_{t=1}^{T} \sum_{i=1}^{N} C_{i, t}^{\mathrm{V} 2 \mathrm{G}}+C_{1} \\ C_{i, t}^{\mathrm{V} 2 \mathrm{G}}=\left|\frac{c}{100}\right| \frac{\Gamma_{i, t}}{E_{i}^{\text {cap }}} C^{\text {change }} \\ \Gamma_{i, t}=\max \left\{0,\left(S O C_{i, t-1}-S O C_{i, t}\right) E_{i}^{\text {cap }}\right\} \end{array}$

1.2 削峰填谷的峰谷差最低

$\begin{array}{c} F_{2}=\min \left[\max \left(P_{t}\right)-\min \left(P_{t}\right)\right] \\ P_{t}=P_{t}^{\text {base }}+\sum_{i=1}^{N} p_{i, t} \end{array}$

1.3 负荷波动最低

$\begin{array}{c} F_{3}=\min \sum_{t=1}^{T}\left(P_{t}^{\text {base }}+\sum_{i=1}^{N} p_{i, t}-P_{\mathrm{av}}\right)^{2} \\ P_{\mathrm{av}}=\frac{\sum_{j=1}^{T}\left(P_{t}^{\mathrm{base}}+\sum_{i=1}^{N} p_{i, t}\right)}{T} \end{array}$

基于削峰填谷的电动汽车多目标优化调度策略研究

一、削峰填谷技术的基本原理与电力系统需求

削峰填谷是一种通过调整电力供需的时间分布来优化电网运行效率的技术，其核心分为两个阶段：

填谷阶段：在负荷低谷时段（如夜间），利用电网富余电能对储能系统或电动汽车进行充电，缓解发电侧压力。
削峰阶段：在负荷高峰时段（如日间），释放储存的电能以补充电网供电，降低峰谷差。
智能控制系统在此过程中起关键作用，通过实时监测电网负荷、电价信号及用户需求，动态调整充放电策略。例如，沙洋县高桥工业园的10MW/100MWh储能电站通过削峰填谷策略，显著提升了新能源电力消纳能力，并缓解了变电站负荷压力。

二、电动汽车作为可调度负荷的特性分析

电动汽车（EV）具备双重属性——可调度负荷与分布式储能资源，其优化调度的潜力主要体现在以下方面：

灵活性：EV的充电时间、功率及荷电状态（SOC）可通过智能算法调节，支持负荷转移与峰谷套利。
储能能力：EV电池可作为分布式储能单元，参与电网调频、调压及备用服务，减少传统机组的调节需求。
用户行为影响：用户充电偏好（如充电时段、SOC需求）直接影响可调度潜力，需通过模糊C均值聚类、长短期记忆网络（LSTM）等模型进行行为预测与分类。例如，基于FCM-SVM的模型可实时判断EV的可调性，分离可调节与不可调节负荷。

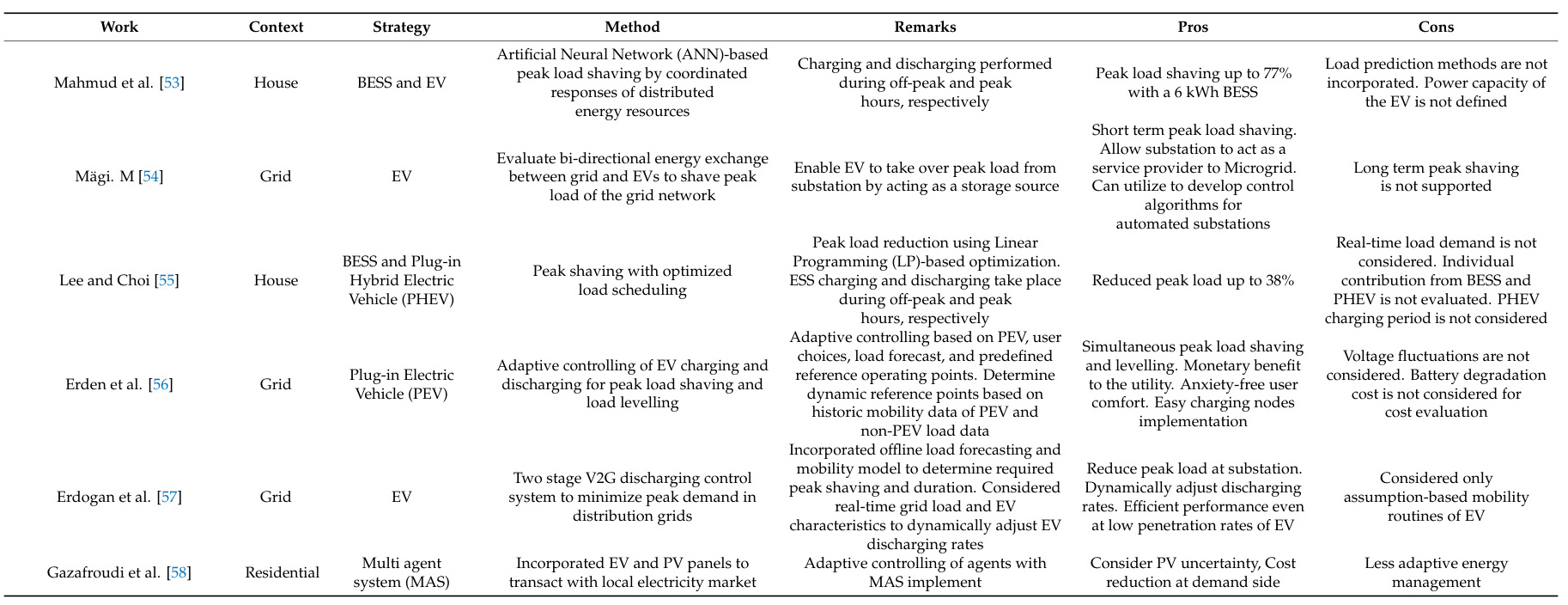
三、多目标优化调度策略的核心要素与目标函数

电动汽车调度需平衡多个相互冲突的目标，典型优化模型包含以下要素：

目标函数：
- 经济性：最小化用户充电成本与电网运行成本。
- 稳定性：降低负荷峰谷差与电网波动。
- 环保性：最大化可再生能源消纳比例，减少碳排放。
- 设备寿命：最小化电池充放电循环损耗。
约束条件：包括EV充电时间窗口、SOC限制、电网容量等。
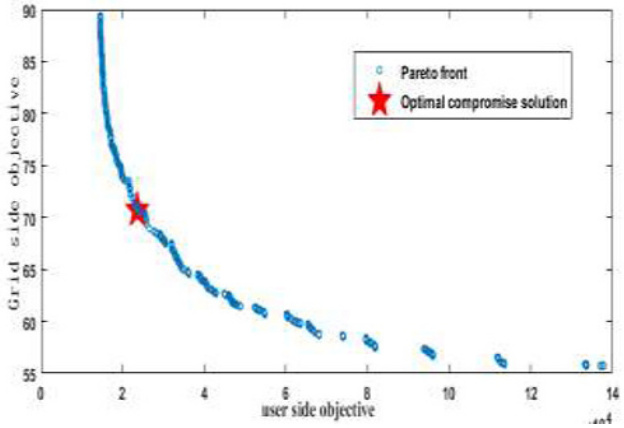
解空间与帕累托前沿：通过多目标优化算法（如NSGA-III、MOPSO）寻找非支配解集，决策者从中选择权衡最优解。例如，改进的多目标粒子群算法（MOPSO）在节能与经济效益的权衡中表现出较高的决策可行性。

四、电动汽车与削峰填谷的协同效应

EV与削峰填谷技术的结合可产生多重协同效益：

提升电网灵活性：EV通过V2G技术参与双向充放电，在高峰时段向电网供电，降低输配电设备扩容需求。例如，湖北计划建设的200万千瓦新型储能项目中，EV集群的调度显著提升了电网调节能力。
促进可再生能源消纳：EV在光伏/风电出力高峰时充电，储存过剩电能；在出力低谷时放电，缓解弃风弃光问题。
经济效益优化：通过峰谷电价机制，用户可降低充电成本，电网运营商减少调峰成本。例如，苏州某充电站通过V2B（Vehicle-to-Building）模式实现峰谷套利，节省电费达30%。
负荷曲线平滑：优化调度后的EV负荷可跟踪电网总负荷变化，降低系统波动性。

五、典型多目标优化算法在调度中的应用

进化算法：
- MOPSO（多目标粒子群优化） ：适用于高维解空间搜索，在微电网调度中可平衡运行成本与环保目标。
- NSGA-III（非支配排序遗传算法） ：通过参考点机制增强解集多样性，适合复杂约束下的帕累托前沿搜索。
混合算法：
- FCM-SVM（模糊C均值-支持向量机） ：用于EV可调性分类，提升调度效率。
- 深度强化学习（DRL） ：结合实时电价与用户行为数据，动态优化充放电策略。
案例应用：某综合能源系统（IES）采用遗传算法（GA）生成帕累托前沿，决策者根据偏好选择调度方案，实现能源效率、经济性与环保性的综合优化。

六、充电负荷预测模型与数据需求

准确的负荷预测是调度优化的基础，需整合以下数据与方法：

数据来源：
- 用户行为数据：充电时间、SOC需求、车型与电池容量。
- 外部环境数据：路况拥堵、天气温度、电价信号。
预测方法：
- 聚类分析：基于行驶里程与时间数据识别路况影响，提升预测精度。
- OD分析法：结合交通网络模拟EV充电需求时空分布。
- 深度学习：LSTM神经网络挖掘时间序列规律，蒙特卡洛模拟处理随机性。
挑战：用户决策的非理性、电池损耗模型的不确定性、多源数据融合的复杂性。

七、电网侧与用户侧利益平衡机制设计

电价激励机制：
- 动态分时电价：引导用户在低谷时段充电，高峰时段放电。
- 两部制电价：固定容量费+可变电量费，降低用户基本用电成本。
市场机制：
- 需求侧响应（DR） ：售电公司聚合EV参与调峰服务，分享收益。
- 虚拟电厂（VPP） ：整合EV、分布式电源与储能，参与电力现货与辅助服务市场。
政策支持：制定标准化通信协议（如桩-网接口）、明确EV在电力市场中的定位、提供设备改造补贴。

八、未来研究方向与挑战

技术层面：
- 提升电池循环寿命与快充能力，降低V2G设备成本。
- 开发兼顾模型驱动与数据驱动的混合预测算法。
市场层面：
- 设计公平的收益分配机制，激励用户参与调度。
- 推动跨区域电力市场建设，扩大调度资源池。
政策层面：
- 完善峰谷电价政策，细化EV参与辅助服务的准入规则。
- 加强跨部门协同（如交通与能源规划），优化充电基础设施布局。

总结

基于削峰填谷的电动汽车多目标优化调度策略，通过整合智能控制算法、用户行为模型与市场机制，可在提升电网稳定性的同时实现经济与环保效益最大化。未来需进一步突破电池技术、数据融合与政策协同瓶颈，推动EV从“被动负荷”向“主动资源”转型，助力新型电力系统建设。

📚2 运行结果

部分代码：

P_EV=sum(P,1); %整合的电动汽车充放电功率
P_M=P_EV+P_base; %综合负荷

P_av=sum(P_M,2)/T;
C1=sum((a*(P_M-P_base)+b*(P_M.*P_M-P_base.*P_base)/2),2); %综合负荷的总成本

M=max(0,((E(:,2:end)/E_cap-E(:,1:end-1)/E_cap))); %电动汽车循环充放电量
C_V2G=abs(c/100)*M*C_change/E_cap; %电动汽车电池退化成本
F_obj_2=sum(C2.*P_EV)+sum(sum(C_V2G));
%F_obj_2=C1+sum(sum(C_V2G));
F_obj_1=sum((P_M-P_av).*(P_M-P_av),2);
F_obj_3=max(P_M)-min(P_M);
F_obj=0.25*F_obj_3/F3+0.25*F_obj_1/F1+0.5*F_obj_2/F2;
ops = sdpsettings('solver','cplex');
rr=optimize(cons,F_obj,ops);