【dfs】【bfs】【链表】 求连通分量 （ssl 1759）

求连通分量

ssl 1759

题目大意

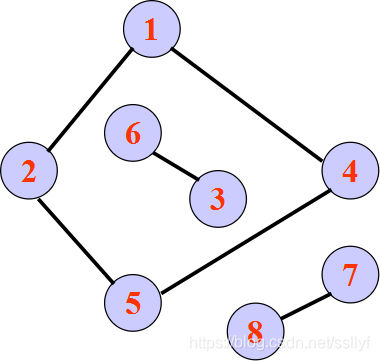
由n个点组成的无向图，求连通在一起的点数最大是多少

---

原题

求一个图的连通分量

Input

n 顶点数(<=100)

边

Output

连通分量

Sample Input

8

6 3

1 2

2 5

5 4

4 1

8 7

0 0

Sample Output

4

---

方法一（dfs 邻接矩阵）

用邻接矩阵的方法来存，再用dfs，要判断到过没

#include<cstdio>
#include<iostream>
using namespace std;
int n,x,y,a[101][101],ans;
bool p[101];
int dfs(int now)
{
	int t=1;//自身
	p[now]=1;//记录
	for (int i=1;i<=n;i++)
	  if ((!p[i])&&(a[now][i]))//到过未，连不连通
	    t+=dfs(i);//累加
	return t;
}
int main()
{
	scanf("%d%d%d",&n,&x,&y);
	while(x&&y)
	{
		a[x][y]=1;
		a[y][x]=1;//正反都要
		scanf("%d%d",&x,&y);
	}
	for (int i=1;i<=n;i++)
	  if (!p[i])
	    ans=max(ans,dfs(i));//求总值
	printf("%d",ans);
}

---

方法二（dfs 邻接表）

用dfs,但是用链表的方法存，搜索时就省了很多时间

#include<cstdio>
#include<iostream>
using namespace std;
int s[101],n,x,y,ans,w;
bool p[101];
struct rec
{
	int ss,next;//ss为连接的数，next和同一个点的另一条线
}a[10005];
int dfs(int now)
{
	int t=1;//自身
	p[now]=1;//已走过
	for (int i=s[now];i;i=a[i].next)//以now为起点的所有边
	  if (!p[a[i].ss]) t+=dfs(a[i].ss);//判断到过没，没到过就去
	return t;
}
int main()
{
	scanf("%d%d%d",&n,&x,&y);
	while (x&&y)
	{
		a[++w].ss=y;//下一个数
		a[w].next=s[x];//下一条边
		s[x]=w;//替换
		a[++w].ss=x;//反过来，做一遍（无向）
		a[w].next=s[y];
		s[y]=w;
		scanf("%d%d",&x,&y);
	}
	for (int i=1;i<=n;i++)
	  if (!p[i])
	    ans=max(ans,dfs(i));//求最大值
	printf("%d",ans);
}

---

方法三（bfs 邻接矩阵）

同样是用邻接矩阵，但用bfs，从每一个位置开始，结果为队列的长度

**#include<cstdio>
#include<iostream>
using namespace std;
int n,x,y,a[101][101],p[101],d[101],ans;
int bfs(int x)
{
	int head=0,tail=1;
	d[1]=x;//入队
	p[x]=1;//记录
	do
	{
		head++;
		for (int i=1;i<=n;i++)
		  if ((!p[i])&&(a[d[head]][i]))//是否可到，到过没
		    {
		    	d[++tail]=i;//入队
		    	p[i]=1;//记录
		    }
	}while(head<=tail);
	return tail;//结果就是长度
}
int main()
{
	scanf("%d%d%d",&n,&x,&y);
	while (x&&y)
	{
		a[x][y]=1;
		a[y][x]=1;
		scanf("%d%d",&x,&y);
	}
	for (int i=1;i<=n;i++)
	  if (!p[i])//判断
	    ans=max(ans,bfs(i));
	printf("%d",ans);
	return 0;
}**

---

方法四(bfs 邻接表)

用bfs和邻接表（二+三），内容基本就是方法二和方法三的合成体

#include<cstdio>
#include<iostream>
int n,x,y,w,ans,p[101],s[101],d[101];
using namespace std;
struct rec
{
	int ss,next;//定义
}a[10005];
int bfs(int now)
{
	int head=0,tail=1;
	d[1]=now;//预处理
	p[now]=1;//记录
	do
	{
		head++;
		for (int i=s[d[head]];i;i=a[i].next)//同一个点连接的不同线
		  if (!p[a[i].ss])//判断到过没
		    {
		    	p[a[i].ss]=1;//记录
		    	d[++tail]=a[i].ss;//入队
		    }
	}while(head<=tail);
	return tail;
}
int main()
{
	scanf("%d%d%d",&n,&x,&y);
	while (x&&y)
	{
		a[++w].ss=y;//后面的数
		a[w].next=s[x];//同一个点的其他线
		s[x]=w;//代替
		a[++w].ss=x;//相反
		a[w].next=s[y];
		s[y]=w;
		scanf("%d%d",&x,&y);
	}
	for (int i=1;i<=n;i++)
	  if (!p[i])
	    ans=max(ans,bfs(i));
	printf("%d",ans);
	return 0;
}

---

方法五The last（bfs 邻接表——$STL$）

个方法四基本相同，但运用了一种鲜为人我知的技术——STL（queue）,改了一些地方

#include<cstdio>
#include<iostream>
#include<queue>
int n,x,y,w,ans,p[101],s[101],d[101];
using namespace std;
struct rec
{
	int ss,next;
}a[10005];
int bfs(int now)
{
	int g,jg=1;
	queue<int>d;
	d.push(now);//在尾端插入
	p[now]=1;
	while(d.size())
	{
		g=d.front();//队头
		d.pop();//队头出列
		for (int i=s[g];i;i=a[i].next)//基本前面的
		  if (!p[a[i].ss])
		    {
		    	jg++;//结果
		    	p[a[i].ss]=1;
		    	d.push(a[i].ss);//入队
		    }
	}
	return jg;
}
int main()
{
	scanf("%d%d%d",&n,&x,&y);
	while (x&&y)
	{
		a[++w].ss=y;
		a[w].next=s[x];
		s[x]=w;
		a[++w].ss=x;
		a[w].next=s[y];
		s[y]=w;
		scanf("%d%d",&x,&y);
	}
	for (int i=1;i<=n;i++)
	  if (!p[i])
	    ans=max(ans,bfs(i));
	printf("%d",ans);//和方法四一样的主程序
	return 0;
}