LS‐设计：高效掩码的位片加密

LS‐设计：用于高效掩码软件实现的位片加密

1 引言

轻量级密码学在过去10年中一直是一个活跃的研究领域。为了优化各种性能标准，已提出了许多创新的分组密码。最近，抵抗侧信道攻击被视为低成本密码算法的额外优化目标，例如算法PICARO [41]和Zorro[20]。这两个方案都旨在实现高效的掩码实现（即所有计算都在共享秘密上进行）。基于此类实现中的性能开销主要来自非线性操作这一观察，Piret 等人[41]首次研究了如何通过考虑非双射S盒来减少其数量。随后，G´erard 等人[20]进一步利用了“不规则”SPN结构，即并非所有状态在每一轮都经过（再次为双射1）S盒。这两个例子相较于AES 里贾德均带来了性能提升，并且随着共享数量的增加，这种优势变得更加显著。

这些先前的工作得出了关于掩码与分组密码中使用的线性/非线性操作之间关系的一些有用观察。在本文中，我们希望通过聚焦于它们留下的两个重要研究方向来补充这些工作。首先从性能角度来看，PICARO 和Zorro均最小化了每加密明文所需的域乘法次数。这是一个自然的方向，因为它带来的改进可同时适用于布尔[45]和多项式[43]掩码方案。然而，进一步针对布尔掩码进行专门优化可能会带来额外收益。例如，轻量级密码PRESENT [7]和 NOEKEON [15]的S盒在 GF（16）中需要三次乘法，这使得它们在多项式掩码方面不如 Zorro和 PICARO 合适。但它们具有高效表示形式，可以最小化与门的数量，这可在布尔掩码实现中加以利用。其次从安全性角度来看，这两种设计基于某种不常见的Feistel/SPN结构（以处理[41],中的非双射S盒以及[20]中每轮S盒数量的最小化）。因此另一个（相当务实的）开放问题是，我们是否可以基于更标准的技术（例如直接利用宽轨迹策略[16]，如同其他轻量级算法那样）来设计适用于高效掩码的密码算法。

在此背景下，我们的研究基于另外两个观察结果。首先，布尔掩码在应用于 GF(2)上的线性运算时特别高效（因为这类运算可以独立地在每个共享上进行）。因此，与许多现有的分组密码不同，将扩散层以查找表的方式实现显得尤为有意义，因为它们可以简单直接地适用于任意数量的共享2。其次，由于我们的重点是软件实现，我们也有强烈的动机追求简单且规则的设计，其中计算始终作用于对齐良好的数据。例如，像PRESENT中那样操作比特和字节会给实现者带来额外挑战（需确保比特操作不会比字节操作泄露更多信息）。这些观察结果共同得出结论：一种采用基于查找表的扩散层、具有高效门级表示的非线性S盒的位片密码，似乎是实现高效布尔掩码软件实现的极佳候选方案。

接下来，我们的贡献有三个方面。首先，我们分别分析了满足前述目标的 S盒和线性层，并从密码分析和高效掩码的角度比较了多种构造方案。有趣的是，本研究的这一部分证实了之前的观察：如果将通过掩码实现的抗侧信道攻击作为分组密码的设计标准，则需要调整线性操作与非线性操作之间的平衡，使其偏向更多的线性操作。此类研究开辟了一个广阔的可能密码空间，我们将其定义为LS‐设计（主要由基于查找表的L盒和位切片S盒组合而成）。随后，我们认 为这类设计在高效掩码方面具有良好的特性。为此，也为具体说明，我们指定了两个128位分组密码实例，并分析了它们针对多种标准密码分析技术的安全性。

在此过程中，我们特别注意了使

2 设计原理

2.1 位切片S盒

在本小节中，我们分析了具有高效位切片表示的多种S盒。我们的比较将考虑不同的大小（即4比特、8比特和16比特），以便在下一小节中研究它们与不同扩散层之间的权衡。同时，我们还将考虑标准密码学属性（如非线性、差分特征和代数次数，其定义见附录A）以及掩码效率。为此，我们遵循[26],中的技术，仅考虑每个S盒所需的与 和 异或 门的数量。如前所述，异或 门的成本在掩码方案的共享数量上线性增长，而与 门的成本是二次增长的（因此在我们的评估中将作为更重要的评判标准）。请注意，由于我们只关注非线性S盒，定义它们的每个布尔函数必须与其他函数线性无关。因此，为了实现这一目标，我们需要的与 门数量至少等于S盒的输出大小。

为何采用位切片？在附录B中，我们回顾了最初在 [26]中提出的执行安全非线性操作的方法，并在 [45]中将其推广到扩展域。从算法 2可以看出，布尔掩码与多项式掩码之间性能的差异（至少部分）可归因于底层非线性操作的实现效率。例如，一个 与门通常可在大多数计算设备上在一个时钟周期内完成。相比之下，域乘法通常需要使用对数/反对数表（如果考虑大域），在嵌入式微控制器上通常需要 20 到 40 个时钟周期 [22]。这些数值可以被改进

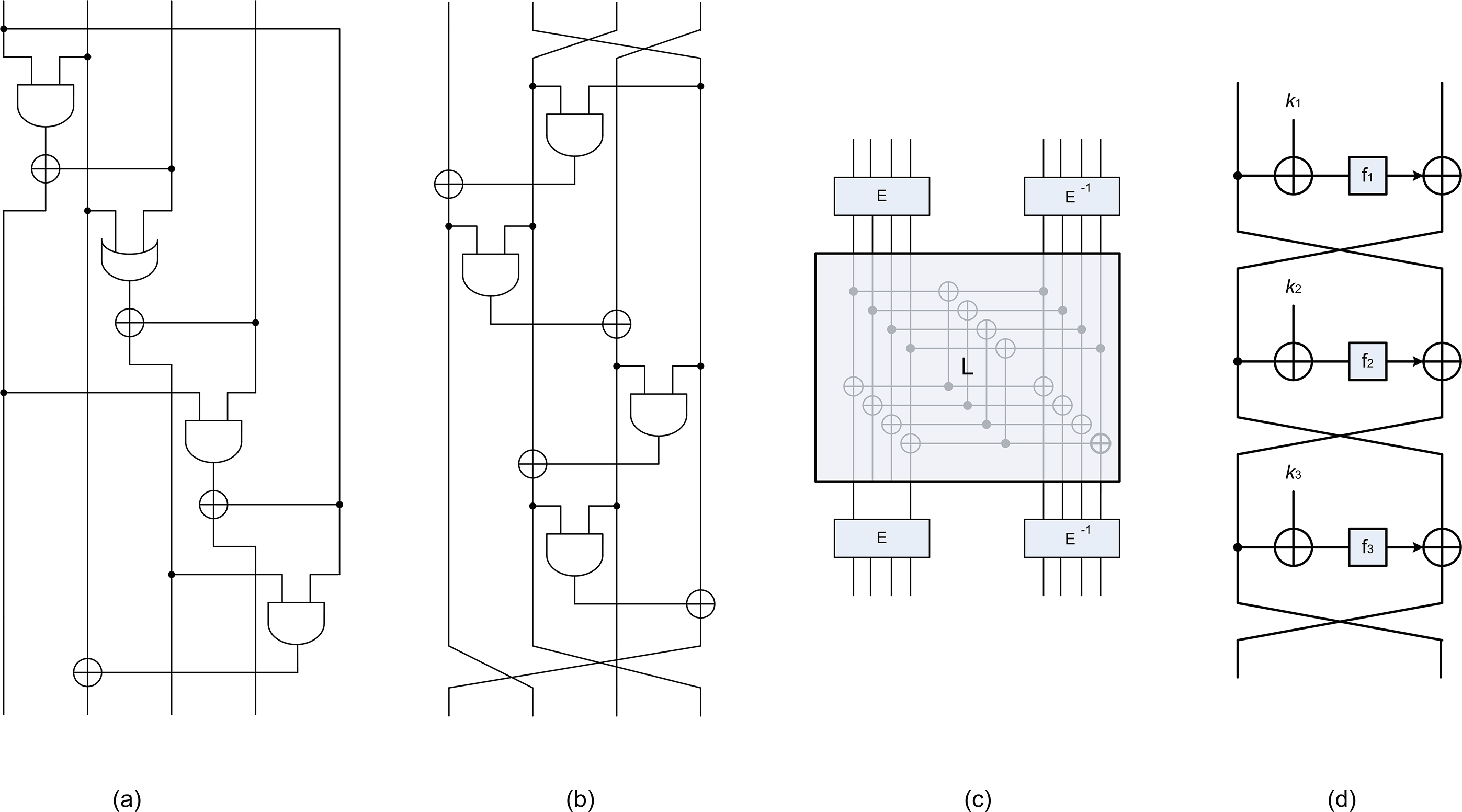具有最优位切片表示的非对合4比特S盒。(b)具有最优位切片表示的对合4 比特S盒。(c)在Whirlpool哈希函数中从4比特S盒构造8比特S盒 [44]。(d)在 MISTY分组密码中从 2s比特S盒构造 s比特S盒的方法[36])

当考虑较小的域时，例如，如果元素的表示少于4位，则乘法可以进行查表；但即使在这种情况下，非线性操作仍需要3到5个周期。因此，接下来我们将研究的在位切片方式下进行门级掩码应能带来性能提升。

我们现在介绍一些具有高效门级表示的S盒。主要挑战在于，随着S盒大小的增加，S盒的枚举迅速变得不可行。此外，寻找大型S盒的最佳门级描述也是一个难题。因此，我们将从4比特S盒的情况开始，因为此时可以进行穷尽分析，然后利用分组密码文献中的启发式方法，将这些4比特S盒扩展为更大的S盒。

4比特S盒。 最优位切片S盒的穷尽搜索可在 [48]中找到。其主要结果是，所谓的“13类”是此目的的最佳选择，可以用4个非线性门和总共9条指令实现，并达到可实现的最佳差分和线性概率。它在图1(a)中表示。它唯一的限制是它不是对合的。我们使用稍大的指令集（包括或非门、与非门以及更多复制指令）进行了类似的穷尽搜索，同时将非线性门的数量限制为4个。结果，我们找到了一个具有与13类相似性质的对合S盒：它在图1(b)中表示。注意，使用托佛利门（定义见 [47]）可以将该S盒视为广义Feistel网络，这解释了其对合性质。

表1. 我们提出的不同S盒的比较。

	# 与	# 异或	size	对合	S的次数	Prdiff	Prlin
NOEKEON	4	7	4	Yes	3	2−2	2−1
类别 13[48]	4	4	4	No	3	2−2	2−1
图 1(b)	4	4	4	Yes	3	2−2	2−1
高级加密标准 [9]	32	83	8	No	7	2−6	2−3
Whirlpool +13类	16	41	8	No	6	2−4.68	2−2
Whirlpool+图1(b)	16	42	8	No	6	2−4.68	2−2
MISTY +Class13	12	24	8	Yes	6	2−4	2−2
MISTY+图1(b)	12	24	8	Yes	5	2−4	2−2
MISTY+ 3/5位S盒	11	25	8	No	5	2−4	2−2
MISTY2+Class13	36	96	16	Yes	13	2−8	2−4

从4比特S盒到更大的S盒。 为此可以考虑多种构造方法，范围从特定方法（将 4比特S盒扩展为8比特S盒）到通用解决方案（将 s‐比特S盒扩展为 2s‐比特S盒）。如同在[20],中一样，我们分析了一些自然的候选方案，并报告了最有趣的结果。

在第一种（特定）情况下，我们考虑了一种来自Whirlpool哈希函数的方案（该方案仅需四个4比特S盒），并通过在两层S盒之间引入一个线性层来推广该方案（见图1（c））。由于我们的目标是最小化与 门的数量，这种方案优于像KHAZAD分组密码中使用六个4比特S盒的方案[1]。

或者，我们研究了MISTY分组密码中使用的Feistel网络[36]，如图1(d) 所示。为了防止在线性和差分密码分析方面存在明显的弱点，至少考虑了三轮结构。这类构造的一个优点是可直接生成对合组件。此外，已经证明，在密钥的平均情况下，此类网络经过三轮操作后会使轮函数的线性和差分概率平方。然而需要注意的是，这种平均效应的影响仅在16比特（或更大）S盒时才会显现（即当递归地两次应用MISTY结构时），因为线性掩模效应的影响从该大小开始才变得显著[40]。对所有具有图1(d)结构的16比特S盒进行穷尽搜索计算量过大，因此我们仅报告所找到的最佳候选结果。对于8比特S盒，我们还进一步研究了由3比特和5比特S盒构建的非平衡Feistel网络（如同MISTY密码中所提出的），这提供了一个略微改进的非对合候选方案（减少了一个与门）。

我们不同的S盒搜索结果总结在表1中。为了便于比较，我们还报告了 NOEKEON S盒以及文献[9]中提出的高级加密标准S盒的位切片表示的相同指标。

2.2 基于表的扩散层

在分组密码的位切片实现中，同一寄存器 i保存多个S盒输入/输出的第 i位。在此背景下，我们关注线性

扩散盒（下文称为L盒），用于在这些寄存器内部混合比特，并可并行地应用于这些寄存器。从实现的角度来看，计算一个L盒仅对应一次表查找操作。然而，与通常的非线性表相比，我们具有更高的灵活性。具体而言，由于该表是线性的，因此可以将其分解为多个较小的表。这有助于仅存储适应目标平台内存特性的表。例如，一个16位L盒可以实现为四个8位到8位查找表和两次异或操作。

我们对扩散层的比较主要基于分支数。借助分支数，我们可以根据宽轨迹策略直接评估任何基于S盒和L盒组合的设计的线性和差分特性。我们将L盒L的分支数定义为：
B(L)= min x≠0( |x| + |L(x)|).
因此，我们的扩散层的线性分支数和差分分支数也均为 B(L)。这保证了在连续两个加密轮次中的任何非平凡路径至少包含 B(L) 个活跃S盒（见[16,定理 1]）。

注意，一个具有分支数 b的 l‐比特L盒等价于一个参数为 2l, l, b 的二元线性码。因此，我们可以利用编码理论的结果来设计我们的L盒，例如 [21]。

8比特L盒。 8位L盒所能达到的最高分支数为5。我们进行了穷尽搜索，找到了 225.2 个具有该分支数的候选方案，其中包括33个对合。它们至少激活 5/16个S盒。

16比特L盒。 16比特L盒可能达到的最高分支数为8。进行穷尽搜索是不可行的，但目前已知存在一些具有参数[16, 8, 8]的码。特别是，可以通过 Reed‐Muller码 RM(2, 5)的系统生成器构造出一种结构化16位对合，其分支数为8，如以下图的左侧部分所示（同一图的右侧给出了一个非对合候选）。这类 L盒在两轮中至少激活四分之一的S盒。

32位L盒。 对于一个32位L盒，最优分支数尚不清楚。已知最佳的编码方案给出的分支数为12，而已知上界表明无法达到高于16的分支数。因此，已知最佳选项将仅激活 12/64的S盒。

我们在表2中展示了已知最佳的L盒扩散层与AES扩散层的比较。这表明L盒扩散层不具有

表2. 线性层的比较。

# S盒	# S盒	活跃S盒
8位L盒	8	5/16 (31.25 %)
16位L盒	16	8/32（25%）
32位L盒 高级加密标准线性层	16	32 12/64 (18.75%) 25/64 (39.06%)

安全性边界与类AES扩散层相当（主要是因为它们在两轮而非四轮上获得），但能够使用位切片实现对于抗侧信道攻击而言是一个重要优势。

或者，如果将状态视为较大域（S盒输出）上的元素向量，则扩散层可以表示为一个二进制矩阵。这种方法此前已被使用过，例如在ARIA的设计中 [33]。

2.3 哪个S盒与哪个L盒搭配？

由 s比特S盒和 l比特L盒的组合直接产生了多种候选的 n= l × s比特密码。在本小节中，我们以64比特情况（使用8比特和16比特L盒）为例，说明这些选择所带来的权衡。

4比特S盒和16位L盒。 利用前述组件，最优的对合S盒需要4个线性操作和4个非线性操作，并达到Prdiff= 2−2和Prlin= 2−1。因此，我们需要至少32个活跃 S盒以实现安全的密码算法。由于每2轮使用16位L盒可产生8个活跃S盒，这对应至少8轮次。在8比特CPU上，将需要64个非线性操作、128次异或操作和 128次查表操作。

8比特S盒和8位L盒。 使用前述的组件，最优的对合S盒需要24个线性操作和12个非线性操作，并达到Prdiff= 2−4和Prlin= 2−2。因此，我们需要至少16个活跃S盒才能实现一个安全的密码算法。由于我们每2轮使用8位L盒会有5个活跃S盒，这大致对应6轮。在8比特CPU上，它将需要72个非线性操作、144次异或操作以及48次查表操作。

有趣的是，我们可以看到第一种选项需要总共320个基本操作，而第二种选项仅需264个。相比之下，第一种选项的非线性操作数量较少，如果考虑具有大量共享的掩码实现，这种优势将逐渐显现。尽管这个例子较为特殊，但它证实了在[20]中已观察到的趋势，即在线更容易掩码的分组密码中，线性操作与非线性操作的数量比例会增加。此外，它还表明一个小的L盒可以激活更大比例的 S盒，但这些更大的S盒通常成本更高（如果要求它们具备良好的密码学性质）。

在此64位比较中，这两种效应的影响程度相似，但结论当然取决于分组密码大小以及我们对大型位切片S盒和L盒的了解。

3 LS‐设计 规范

根据前一节内容，我们可以将LS‐设计定义为由算法1指定的分组密码族。该描述直接表明简洁性和规则性是此类密码的一个重要优势：实例可以通过选择一个位切片S盒S、一个L盒L、轮数 Nr以及常量 C（r）来确定。在接下来的章节中，我们将考虑两个128位的LS‐设计实例，以说明其抗密码分析安全性和良好的实现特性。选择该位大小的原因既有来自[49]的观察结果，也是为了能够与NOEKEON进行比较（NOEKEON是迄今为止发布的最高效的位切片表示密码之一）。

算法1. 具有 l‐位L盒和 s‐位S盒的LS‐设计（n= l · s）

x ← P ⊕ K;  x是一个 s× l位矩阵
对于 0 ≤ r< Nr执行
    对于 0 ≤ i< l执行 S盒层 
        x[i, ]= S[x[i, ]];
    结束循环
    对于 0 ≤ j< s 执行 L盒层
        x[, j]= L[x[, j]];
    结束循环
    x ← x ⊕ K ⊕ C(r); 密钥加法和轮常数
结束循环
返回 x

对合实例（Robin）。 我们采用表1中记为“MISTY + Class13”的S盒以及第2.2节中的对合L盒。该密码算法有16轮，常数计算为L(i) 0… 0]，其中 i为轮索引。

非对合实例（Fantomas）。 我们采用表1中记为“MISTY+ 3/5位S盒”的S盒以及第2.2节中的非对合L盒2.2。该密码算法共12轮，使用的常数与Robin相同。

4 安全评估

我们现在研究LS‐设计的安全属性，试图首先得出适用于我们密码族的一般性结论。为了具体说明，我们还将考虑与前述实例相关的具体声明。在这方面，我们注意到Robin和Fantomas的设计目标略有不同。具体而言，前者旨在实现与NOEKEON相似的安全裕度，而后者主要是为了说明选择对合组件对LS‐设计可达到的效率极限所产生的影响。请注意，在这两种情况下，我们的目标都是单密钥安全性（即在我们的声明中排除相关密钥攻击和选择密钥攻击）。特别地，如果可以通过密钥差来纠正状态差，则每轮存在一个仅包含单个活跃S盒的简单相关差分。

4.1 抵抗线性与差分密码分析的安全性

如第2.2节所述，密码的结构对差分特征的最大概率和线性轨迹的最大偏置给出了一个简单的上界。任何两轮轨迹至少激活 B(L) 个S盒，这给出了任意 2r轮轨迹的以下界：
Prlin(2r) ≤ Prmax lin(S)r·B(L), Prdiff(2r) ≤ Prmax diff(S)r·B(L). (1)
根据第3节的参数，得到：
Prlin(2r) ≤ 2−16·r, Prdiff(2r) ≤ 2−32·r.
这些界可以防止基于超过8轮次的轨迹的简单线性和差分攻击。我们在Robin（分别地， Fantomas）中使用16轮（分别地，12轮），以获得良好的（分别地，较不保守的）安全裕度。现在我们研究这些界的紧性，以及如何构建最优的差分/线性轨迹。

Robin的乘积轨迹。 为了研究差分和线性轨迹，我们首先考虑一组特殊的状态，这些状态可以表示为一个 s比特向量（对应S盒输入，用希腊字母表示）和一个l比特向量（对应L盒输入，用拉丁字母表示）的张量积：
α ⊗ x=
⎡ ⎢⎢⎢⎢⎢⎣
α0x0 α0x1 α0x2 α0x3 α0x4 ··· α0xl α1x0 α1x1 α1x2 α1x3 α1x4 α1xl α2x0 α2x1 α2x2 α2x3 α2x4 ··· α2xl
… … ......
αsx0 αsx1 αsx2 αsx3 αsx4 ··· αsxl
⎤ ⎥⎥⎥⎥⎥⎦ .
对于这些状态，S盒层和L盒层独立作用：
S− layer(α ⊗ x)= S(α)⊗ x, L− layer(α ⊗ x)= α ⊗ L(x).
因此，差值和线性掩码具有相同的行为。具体而言，我们可以构建差分特征 （或线性轨迹），其中差值（或选择掩码）表示为张量积。特别地，如果 L [x]= y 且 α β 以概率 p 通过 S 盒，则 x ⊗ α y ⊗ β 以概率 p |x| 通过一轮，其中 |x| 表示 x 的汉明重量。

当密码算法构造成对合时，我们进一步得到 β α ，其概率为 p，且L [y]= x，因此经过一轮后以概率 p |y|得到 y ⊗ β x ⊗ α，从而形成一个两轮迭代轨迹（如图2中的玩具示例所示）。如果 α、 β、 x和 y被最优选择，则该路径达到公式(1)的安全边界，表明该边界是紧的。使用Robin的参数， α和 β的最优选择给出 p= 2−4，而 x和 y的最优选择给出 |x| + |y| = 8。这直接导致一个概率为 2−32（或8轮时为 2−128）的两轮迭代差分特征，以及一个偏置为 2−16（或8轮时为 2−64）的两轮迭代线性轨迹。

截断差分。 由于L层和S层在乘积状态上独立操作，因此存在许多具有相同活跃 S盒但输入和输出不同的路径。只要某一轮中所有S盒具有相同的输出差分，该状态即为乘积状态，且所有这些差值均贡献于同一条截断路径。此类乘积状态的空间非常小，因此我们可以利用乘积路径穷尽地搜索最优截断差分。我们注意到可能存在更优的截断路径，但当考虑对合时，乘积路径似乎是主导的。

对于Robin，最佳的截断路径从单个活跃S盒开始，并交替出现1个和7个活跃S盒。具有单个活跃S盒的轮次遵循截断路径的概率为1，而具有7个活跃S盒的轮次在输入差分为随机的情况下其概率为 2−28.5（如果来自前一轮，则概率略有偏斜）。针对8轮和9轮的最佳此类路径概率为 2−112.1，而针对10轮和11轮的最佳路径概率为 2−139.8。这些结果可用于如下截断差分攻击：若取一个具有单个活跃S盒的状态对，在9轮之后以概率 2−112仍保持单个活跃S盒（相同位置）。通过使用包含256个明文的结构，其中120比特设为固定值，最后一个S盒输入取所有可能值，可得到 215个具有单个活跃S盒的不同对。若收集297个这样的结构，则可获得 2112个输入对，并预期其中有一对在输出时仅有一个活跃S盒。由于此类事件在随机函数下发生的概率仅为 2−120 ，因此在 2112个对之后不会出现误报。因此，我们得到了一个针对9轮的区分器，其成本为 2104。此外，预计可通过部分解密将此区分器扩展到更多轮次。

从对合组件到非对合组件。 如果我们不限制设计使用对合的S盒和L盒，则可以期望由公式(1)给出的界不是紧的。更准确地说，我们预期不应存在任何截断路径能够以每个S盒转换的最优概率达到最少活跃S盒数。为此，我们首先对截断路径中的活跃S盒数量进行计数。也就是说，对于每个状态，我们只关心哪些列是非零的，并构建所有可能的转换。在此背景下，需要注意的是，扩散层的截断输入可能产生多种不同的截断输出，并不一定会线性地行为。例如，如果我们从00101000开始，则必须考虑五种可能的转换：
L[00101000], L[00100000] ∨ L[00001000], L[00101000] ∨ L[00100000], L[00101000] ∨ L[00001000], L[00101000] ∨ L[00100000] ∨ L[00001000].

更一般地，可能的转换具有以下形式：
x0 ∨ x1 ∨… ∨ xl L[x0] ∨ L[x1] ∨… ∨ L[xl]
非线性转换通常会导致状态中出现更多活跃列，但非线性带来的额外自由度使得其路径优于仅包含线性转换的乘积路径。对于 l= 8，我们对所有分支数为5的L盒进行了穷尽搜索，发现最佳的L盒在16轮次内至少能产生53个活跃S盒 （而当L是对合时，仅能产生40个活跃S盒）。对于 l= 16，为固定L盒构建所有可能的转换本身已是一个难题，因此我们无法测试大量不同的L盒。我们通过置换RM(2, 5)系统生成器的行和列进行了一次随机搜索，该生成器用于第2.2节。我们找到的最佳非对合L盒（见第2.2节）在12轮次内可产生至少64个活跃S盒的截断路径。更准确地说，我们可以计算使用对合L盒和我们找到的最佳非对合 L盒时活跃S盒的最小数量如下：

轮次	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
对合的	1	8	12	16	20	24	30	34	40	46	52	58	64	74	80	86
非对合的	1	8	12	16	25	32	33	41	48	49	55	64	76	80	86	92

如果我们考虑一个具有 l= 16和 s= 4的64位密码，我们可以进一步进行分析，并找到具有完全实例化差分的最优差分路径。我们预计这将再次改进路径概率的上界，因为通常无法选择某个特定差分使得所有S盒转换都具有最大概率。我们使用A*∗算法[24],并结合松井的分枝限界算法[35]的一些额外思想进行了此次搜索。在A*∗中，我们使用最优截断路径作为对未来路径成本的启发式估计，并通过计算轮数递增的最优路径来对其进行优化。一旦我们知道最优实例化 r轮路径的概率，如果某些截断的 r轮路径预期具有更高的概率，我们会更新该启发式估计。通过这样做，我们发现某些L盒和S盒的选择可使6轮路径的概率至多为 2−64，8轮路径的概率至多为 2−90（例如第2.2节中的候选L盒 与S盒 S={6, 1, 0, 7,E, 4, F, D, 5, B, 2, C, 3, 8, A 9}）。这些值应与当L和 S被限制为对合变换时的 2−48（分别地 2−64）以及之前使用截断路径分析方法得到的相同组件的界 2−56（分别地 2−80）进行比较。这表明，对于这些参数 （l= 16和s= 4），基于对合组件的LS‐设计需要大约 4/3倍于非对合组件的 轮次才能达到相似的安全级别。该计算耗时数天并使用了数十千兆字节内存。我们认为，这一结果很好地反映了对合密码与非对合密码之间相对安全性的趋势，即使对于更大的S盒也应成立，尽管在实践中我们无法对 l= 16和 S={6, 1, 0, 7, s= 8运行最优路径的搜索。

应用于 Fantomas。 通过使用我们对截断轨迹的搜索，我们找到了Fantomas上线性和差分轨迹的以下界：
Prlin(6) ≤ 2−56, Prdiff(6) ≤ 2−112, Prlin(7) ≤ 2−68, Prdiff(7) ≤ 2−136.
这些界表明，对Fantomas的简单线性与差分攻击仅可能在6轮或更少轮次的路径上奏效，因此我们拥有6轮的安全裕度。我们认为此界并不紧，这一点已通过我们对64位LS‐设计上实例化路径的分析得到验证（但在实践中无法对 Fantomas进行类似的分析）。此外，我们注意到，对Robin的最佳攻击基于对应多个简单路径的截断差分，但这种效应在Fantomas中将非常有限，因为其最优路径不具备乘积路径的强结构特性（在6轮情况下，使用一组乘积路径的最优截断差分的概率为 2−117）。

不可能差分。 最后，我们搜索了一类不使用S盒性质的不可能差分，即仅考虑每一轮中哪些S盒是活跃的，并结合线性层的可能转换以及S盒为双射这一事实进行分析。该搜索方法类似于上述截断路径的搜索，其中最困难的部分仍然是构建所有通过L操作的可能转换。我们发现，在Robin和Fantomas中（在此类别下）最长的不可能差分仅跨越三轮次。对于Robin，存在48420种不可能的输入‐输出模式，一个示例如 0000000000000001 000000000000010所示；对于 Fantomas，存在35951种不可能差分，一个示例如 0000000000000001 000000000000001所示。我们可以将此结果与高级加密标准上的类似结果进行比较：目前已知最好的不可能差分属于此类别，并跨越四轮次。由于我们的扩散层在每一轮都混合了全部16个S盒输入，因此出现更短的不可能差分是合理的。

4.2 针对Even‐Mansour密码的通用攻击

1991年，Even和Mansour提出了一种简单的分组密码设计，仅使用一个置换和两个不同的密钥值[19]。该设计后来在[19]中被重新研究，并通过使用 n个置换和 n+ 1个密钥值扩展为密钥交替密码。这类密码的一个特例是单密钥 Even‐Mansour（SEM）方案，其定义是使用 n个置换与一个密钥结合。由于其简洁性，这些设计引起了多位密码分析者的关注，已有多种研究成果适用于它们的通用版本[12,17,18]或特定实例，如LED或佐罗[23,27,37,38]。

由于LS‐设计对应于SEM方案，我们讨论了这些先前结果在我们案例研究中的适用性。特别是，尽管我们并未声称具有针对相关密钥和选择密钥攻击的安全性，但我们对此进行了简要分析

Δ Δ
F1 Δ
Δ
Fn Fn
0
概率 1
Δ′ Δ

以通用方式描述对抗场景。从选择密钥差分开始，攻击者不仅可以控制 n位输入值，还可以控制 n位密钥值。因此，相比标准差分密码分析，他所拥有的自由度翻倍（达到 2n）。我们从第4.1节可知，LS‐设计的最佳差分特征的概率为：
Prdiff(2r) ≤ Prmax diff(S)r×B(L).
因此，如果2−2n ≤ Prdiff(2r)，则可以对 2r轮次发动攻击。以Robin为例，最佳的两轮特征的概率为2−32，且自由度等于256。因此，在最坏情况下，可能利用所有自由度攻击 8 · 2= 16轮次。在相关密钥场景中也可以得出类似的观察结果。具体而言，通过应用[38],的结果，对于LS‐设计而言，覆盖两轮的最佳差分特征可以扩展到三轮（如图3所示）。因此，实现 n比特安全性的所需轮数将增加50%。

4.3 代数攻击

在代数密码分析中，密码算法被表示为一个大型非线性方程组（通常在 GF(2)上），并试图求解该方程组。尽管任何算法都可以用多变量方程来描述，但求解这些方程对于二次方程而言已经是NP难问题。代数密码分析的精确复杂度难以评估，通常通过展示方程组的大小和未知数的数量，并结合密码算法的代数次数进行分析，来论证其针对此类攻击的安全性。

LS‐设计中的S盒可以用与非线性门数量相同的方程数来描述。设 e表示非线性门的数量， l表示L盒的大小， Nr表示轮数。那么，一个固定密钥LS‐设计的整个系统由(Nr· e·128/l)个二次方程组成，包含(Nr · 128 · 2)个变量。对于 Robin，这对应于4096个变量中的3072个方程；对于Fantomas，则是3072个变量中的2112个方程（高级加密标准有2560个变量中的6400个方程）。考虑到求解小规模高级加密标准变体所需的时间和内存复杂度（如[10]中所示），我们认为这些数值足以使这两个实例抵御代数攻击。关于代数次数，我们使用了工作[8]来计算累积代数次数

4.4 其他密码分析

我们使用轮常数使各轮次互不相同，以防止滑动攻击[6]（这些攻击基于轮函数的自相似性）。旋转密码分析[30]是对基于加法‐旋转‐异或（ARX）的分组密码的一种强大攻击技术。但由于LS‐设计中应用了S盒操作，使得此类攻击难以成功。积分密码分析或平方攻击[13]主要针对面向字的密码，但也可适配到位切片密码。我们的分析表明，最多可对Robin或Fantomas的4轮进行此类攻击 （这也保留了充足的安全裕度）。最终，回旋镖攻击[50]假设我们能在目标算法中找到(2·r1+1)轮和(2·r2+1)轮的两个特征。通过使用公式(1)，我们可以将这些概率近似为Pr(2· r+ 1) ≤Prmax diff(S)r×B(L)+1。因此，回旋镖区分器的概率变为Prmax diff(S)2·((r1+r2)×B(L)+2)，该值必须优于 2−n。将Robin或Fantomas的参数代入此方程，我们得到2(r1+ r2) + 2< 5.5，且该攻击最多适用于五轮。因此，回旋镖攻击不应成为LS‐设计的关注问题。

5 性能评估

LS‐设计的主要目标是为8位微控制器实现高效且安全的软件实现。因此，我们首先报告了在Atmel ATmega644p微控制器上对Robin和Fantomas以及高级加密标准、佐罗、PICARO和NOEKEON3进行掩码保护后的实现性能。图4中的结果（针对掩码方案中不同共享数量）显示，Robin和NOEKEON（两者均为对合密码）的性能非常接近。这些结果证实，针对布尔掩码优化的位切片密码能够实现比此前使用高级加密标准、佐罗 或PICARO所获得的更高效的实现。同时，它们也说明了通过采用非对合组件（例如在Fantomas中）可以获得额外的性能提升。结合高度规则化的设计以及所有操作均作用于良好对齐的8比特数据的特点，我们认为该评估支持以下结论：LS‐设计是具备抗侧信道攻击潜力的有前景的密码算法。

此外，我们还发现LS‐设计在具有大型SIMD单元的桌面CPU上非常高效，至少对于无保护实现而言是如此。以Fantomas在计数器模式下的情况为例，我们可以并行处理多个输入，并充分利用SIMD单元的完整宽度。下面我们详细描述一种使用SSSE3指令和128位寄存器的实现方式。我们将使用16个SSE寄存器并行计算16个Fantomas实例（每个实例使用不同的明文），每个寄存器包含来自每个Fantomas副本的一个字节（8个寄存器用于高字节，另外8个寄存器用于低字节）。S盒层通过128位宽的按位操作并行计算两组共128个S盒；这需要 96条指令。对于L盒层，我们使用pshufb指令作为4位到8位查找表。16比特L盒被分解为八个4位到8位查找表和6次异或操作4；我们的实现在并行计算16个线性层（即128个16比特L盒）时需要280条指令。根据这些数据，我们在Core i 7处理器（Nehalem微架构）上实现的Fantomas运行速度达到6.3周期/字节 （针对长消息）。得益于pshufb指令，L盒层不会受到缓存时序攻击的影响。

作为对比，K¨asper和Schwabe [28]的位切片AES实现对于相同数量的S 盒和线性层分别需要326和102个周期（完整的AES在同一CPU上为6.9周期/字节——这是该CPU上已知最快的AES实现）。一方面，我们的S盒比AES S盒更容易以位切片方式实现，因为这正是我们的设计目标之一。另一方面，我们的线性层针对基于查找表的实现进行了优化，因此比AES的线性层更复杂。尽管它仍然可以相当高效地实现，但在该实现中已成为主导因素。这表明LS‐设计能够达到可比较的性能

表3. 长消息的并行模式实现结果。

	Fantomas Robin	高级加密标准	标准
	Fantomas Robin	无AES‐NI[28]有AES‐NI
ARM Cortex A15	14.2	18.1	17.8
Atom	33.3	43.5	17
酷睿i7 Nehalem	6.3	8.1	6.9
酷睿i7 Ivy Bridge	4.2	5.5	5.4

对于高端CPU上的高级加密标准，排除使用硬件AES指令的实现（表3）。我们还期望在Atom或ARM Cortex‐A CPU上获得合理的性能，这些CPU用于某些嵌入式系统，并具备良好的向量引擎和置换指令（分别为SSSE3和NEON）。此外，最新的英特尔CPU支持使用AVX2操作的256位宽SIMD操作；我们预计这将带来更佳的性能5。

6 开放性问题

本文介绍了LS‐设计，作为一类安全且高效的分组密码，具有适用于掩码实现的良好特性。由于其具体实例化主要依赖于选择优良的S盒和L盒，一个自然的研究方向是寻找更优的此类组件，特别是针对较大的位大小（例如，S盒8比特及以上，L盒32比特及以上）。在这些方面的改进将直接带来更优化的密码算法。此外，我们目前的研究主要考虑了软件实现。但Robin和Fantomas高效的门级表示使它们也可能适用于硬件实现。因此，研究它们的阈值实现，并将所得性能与其他在此场景下高效的算法（例如再次使用NOEKEON[39]或 FIDES[5]等更新的设计）进行比较，将是十分有意义的。