本资源仅供学习交流,严禁用于其它用途!
优化设计基础
一、 overview of optimization

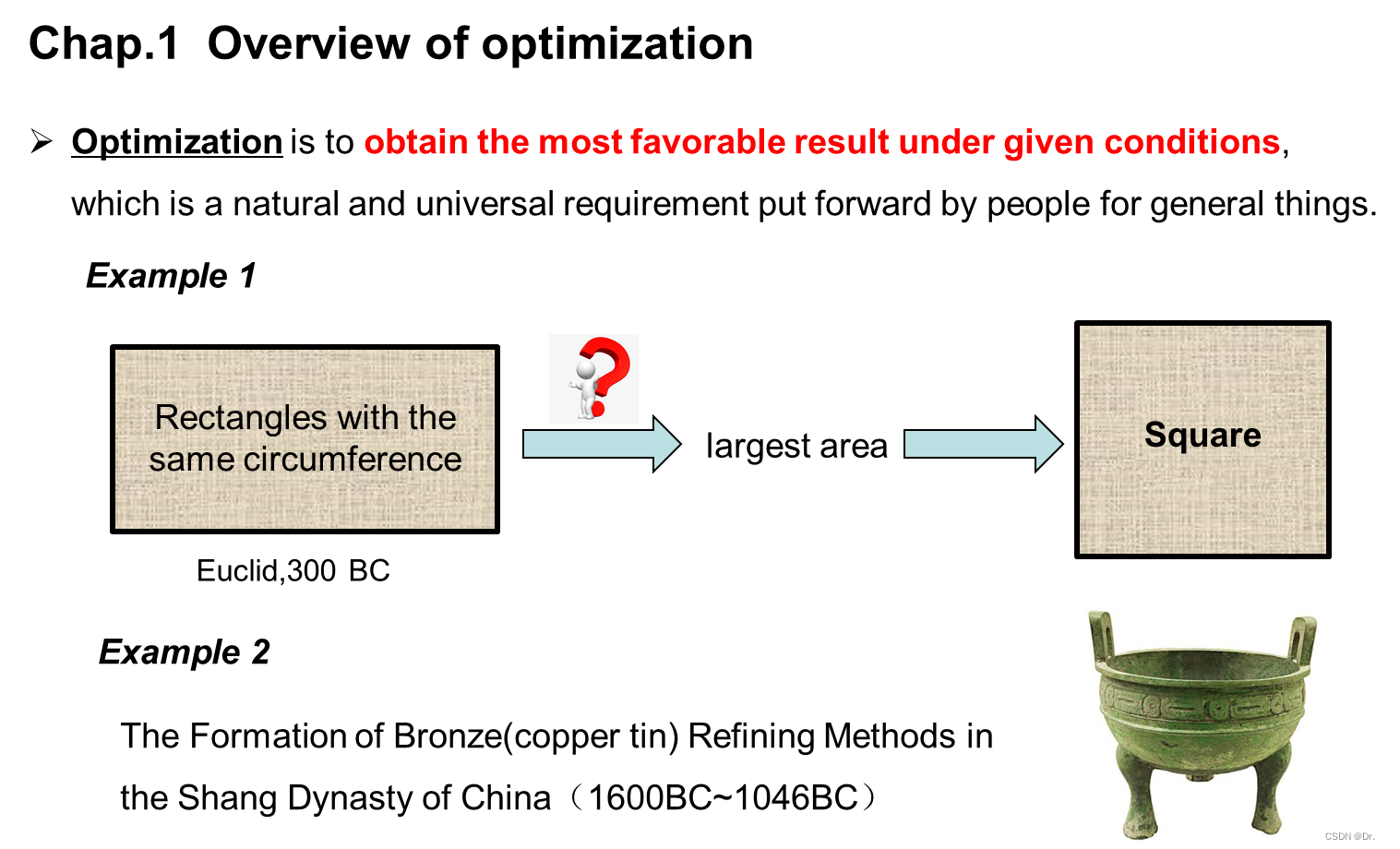



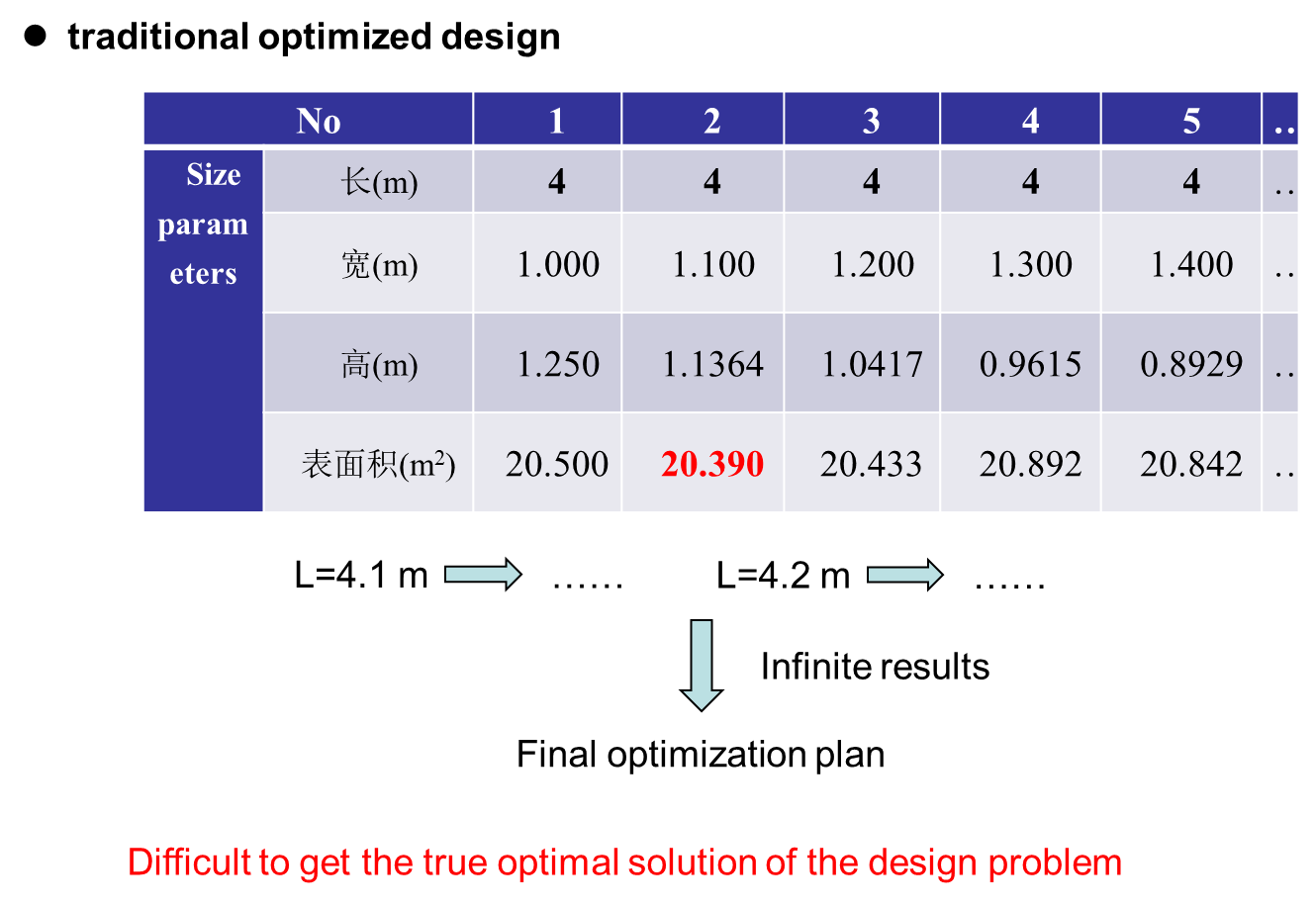
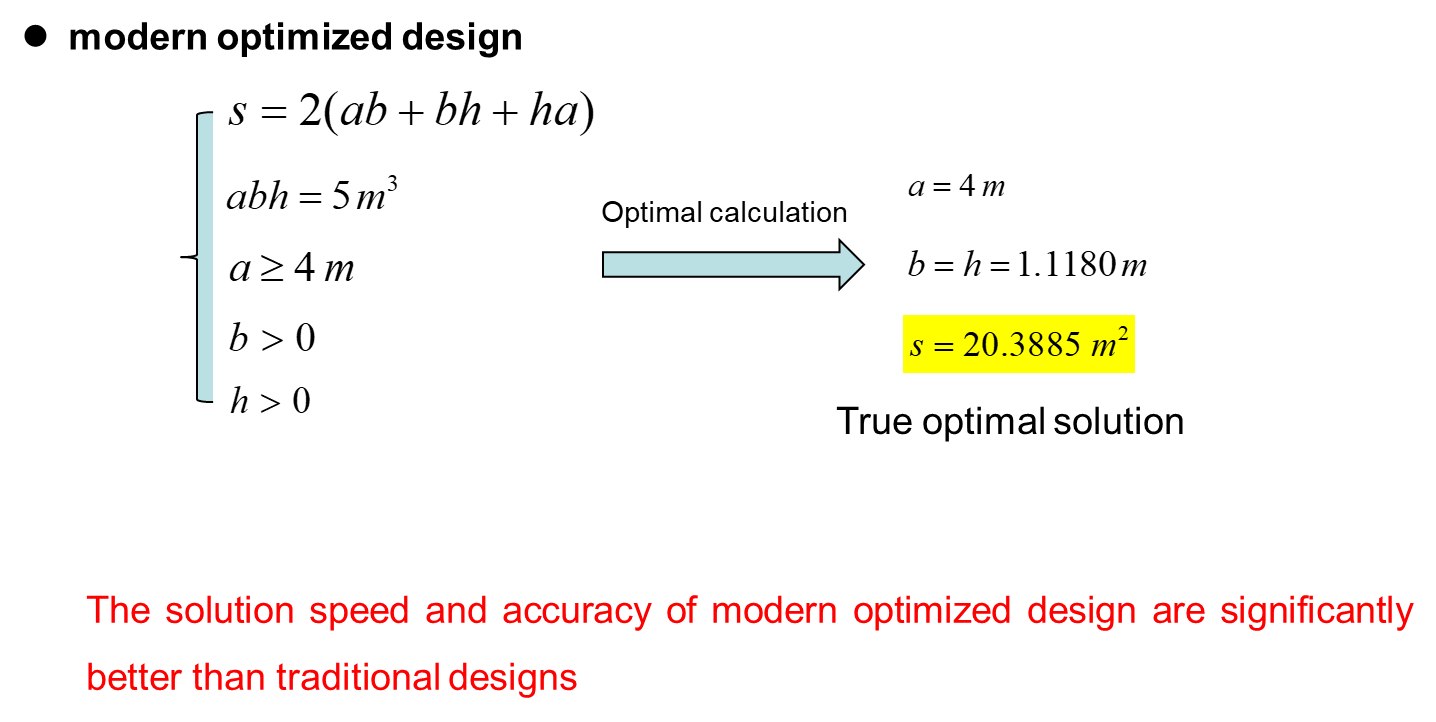
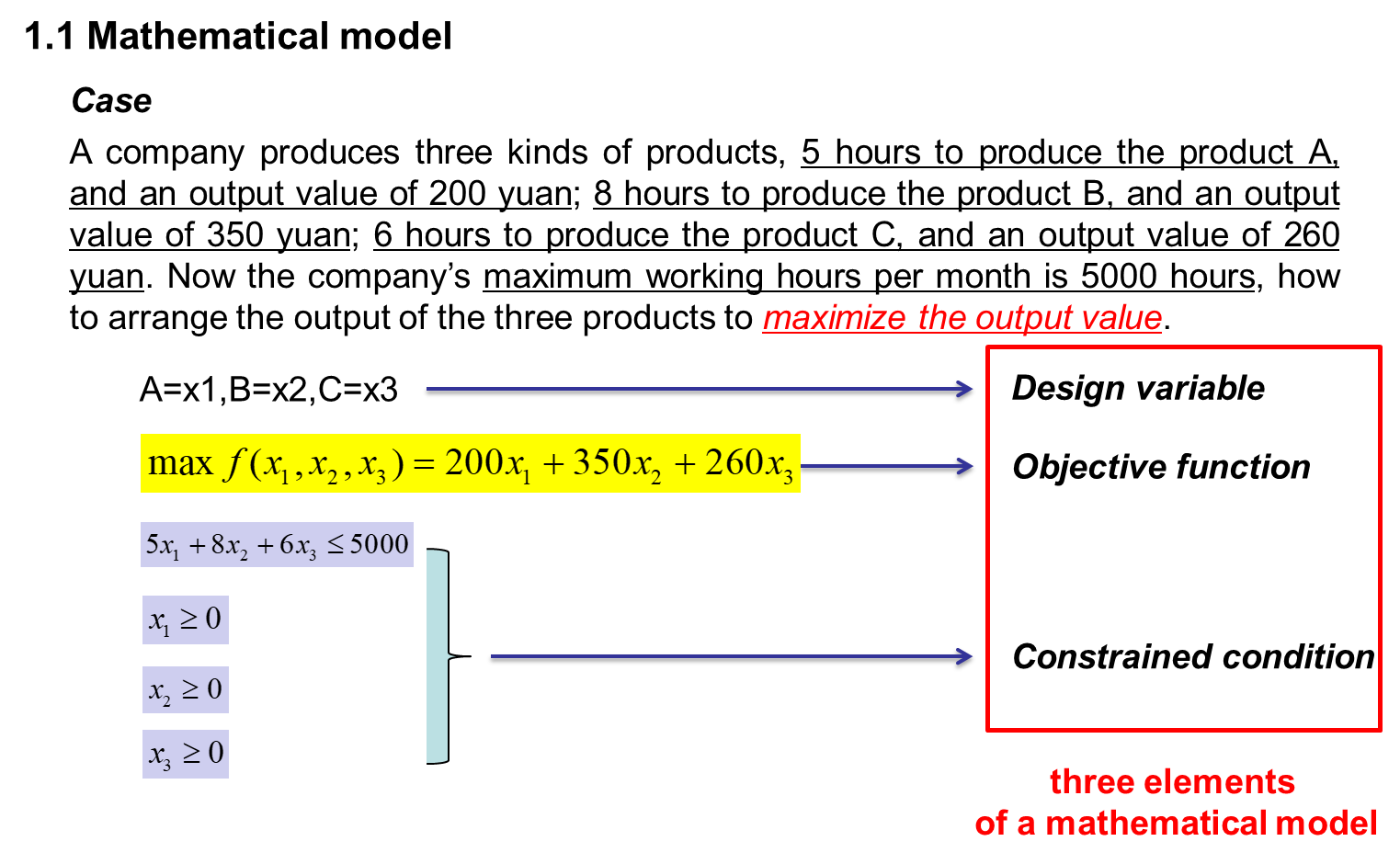
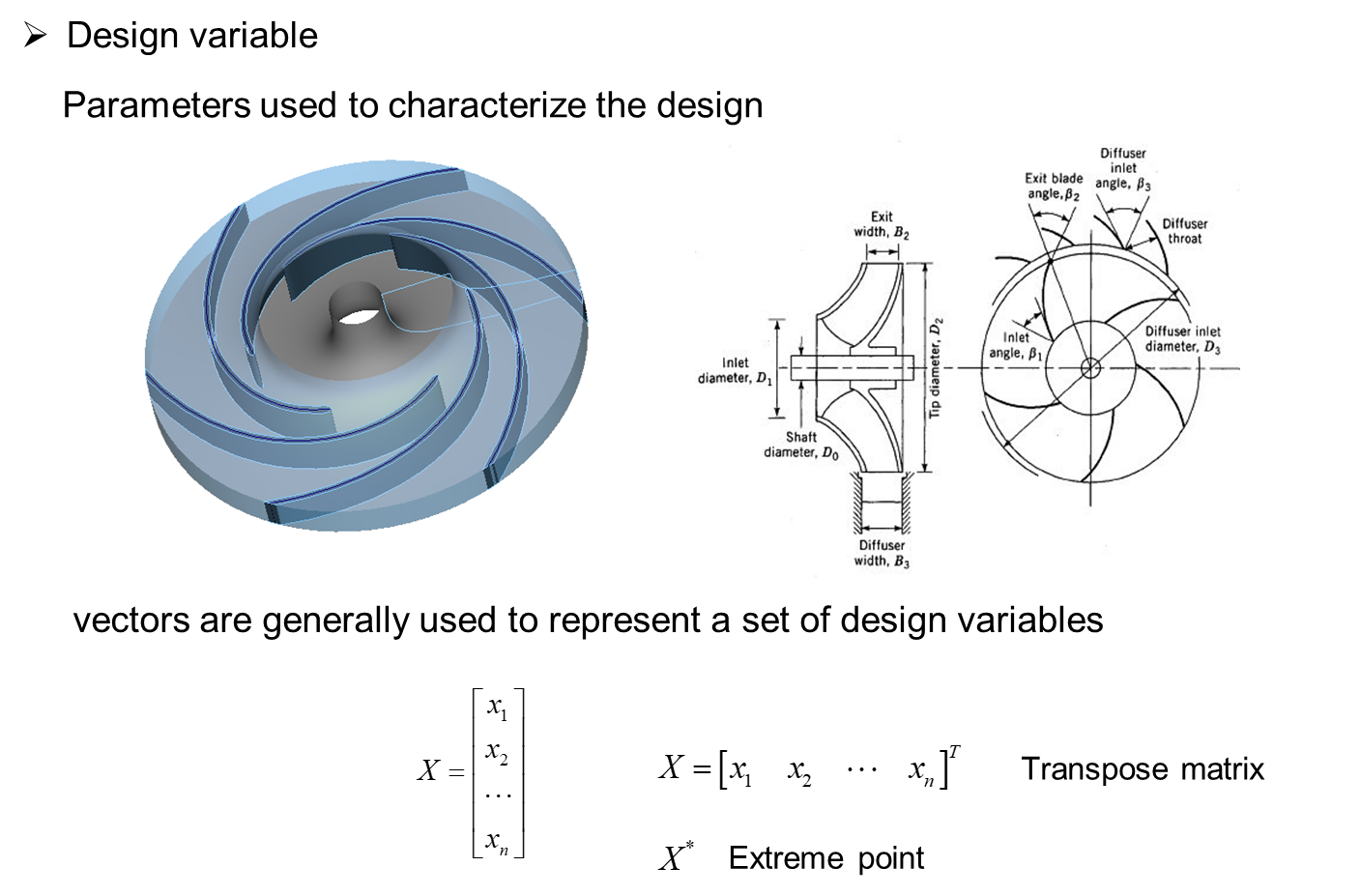

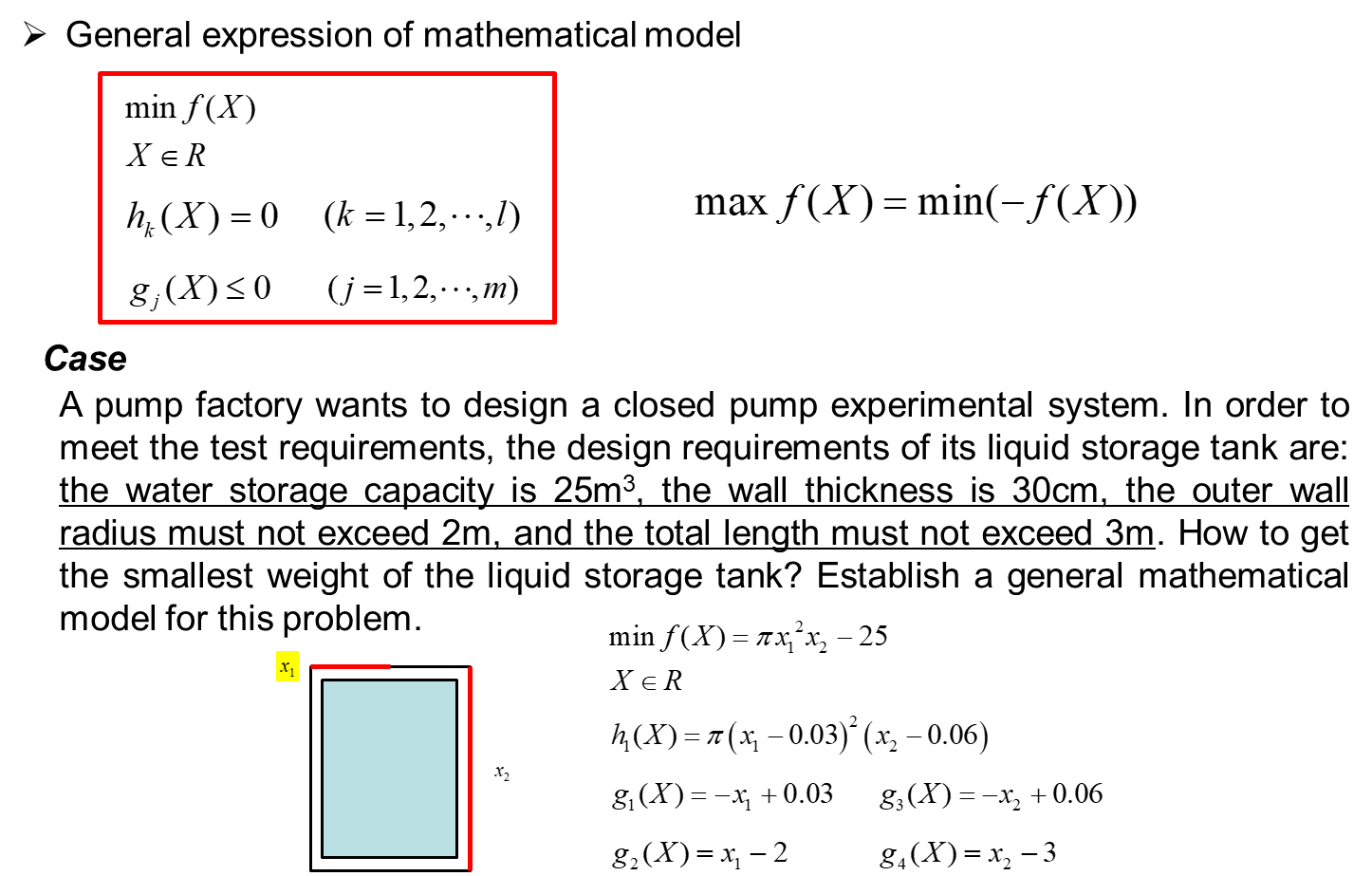
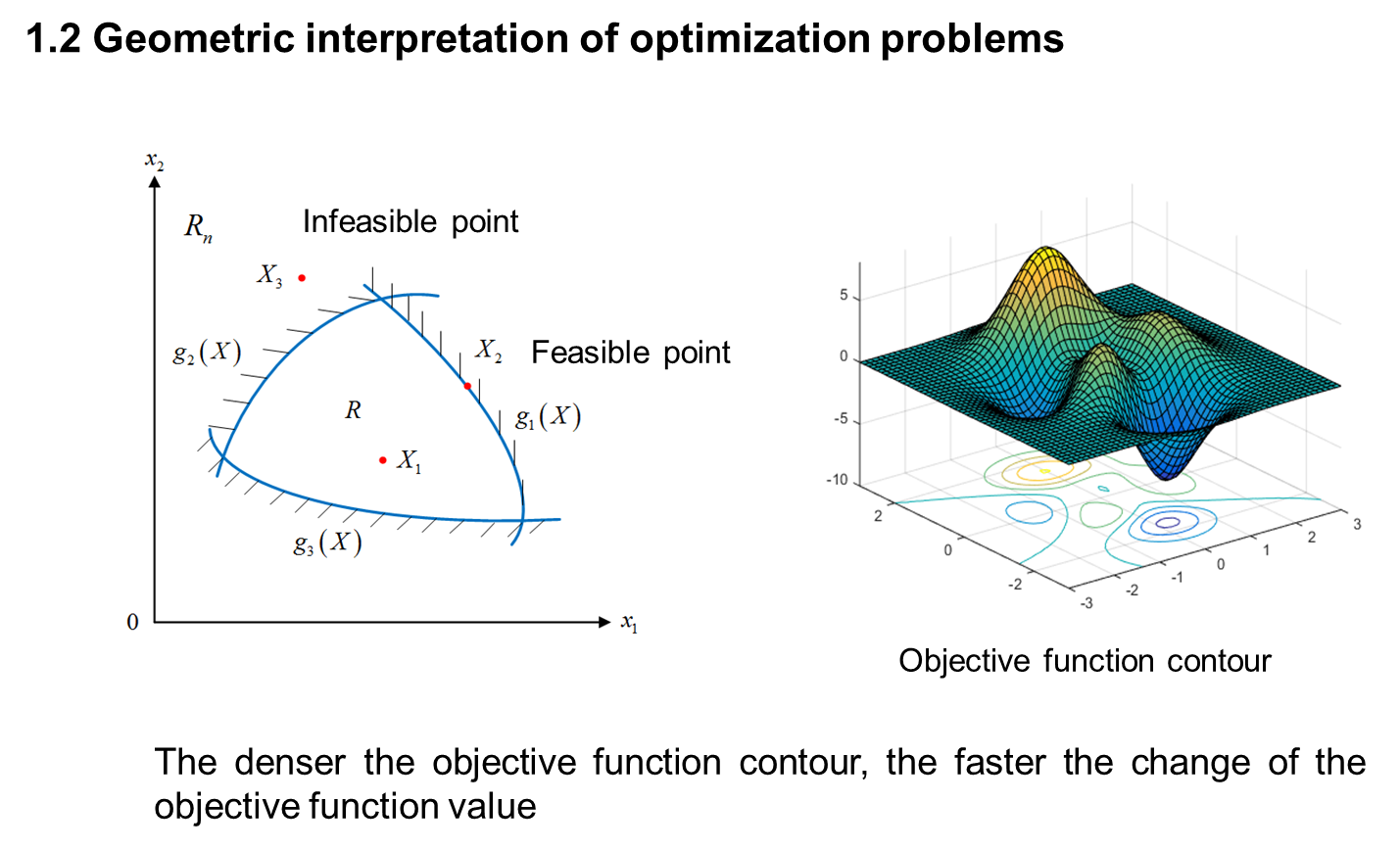

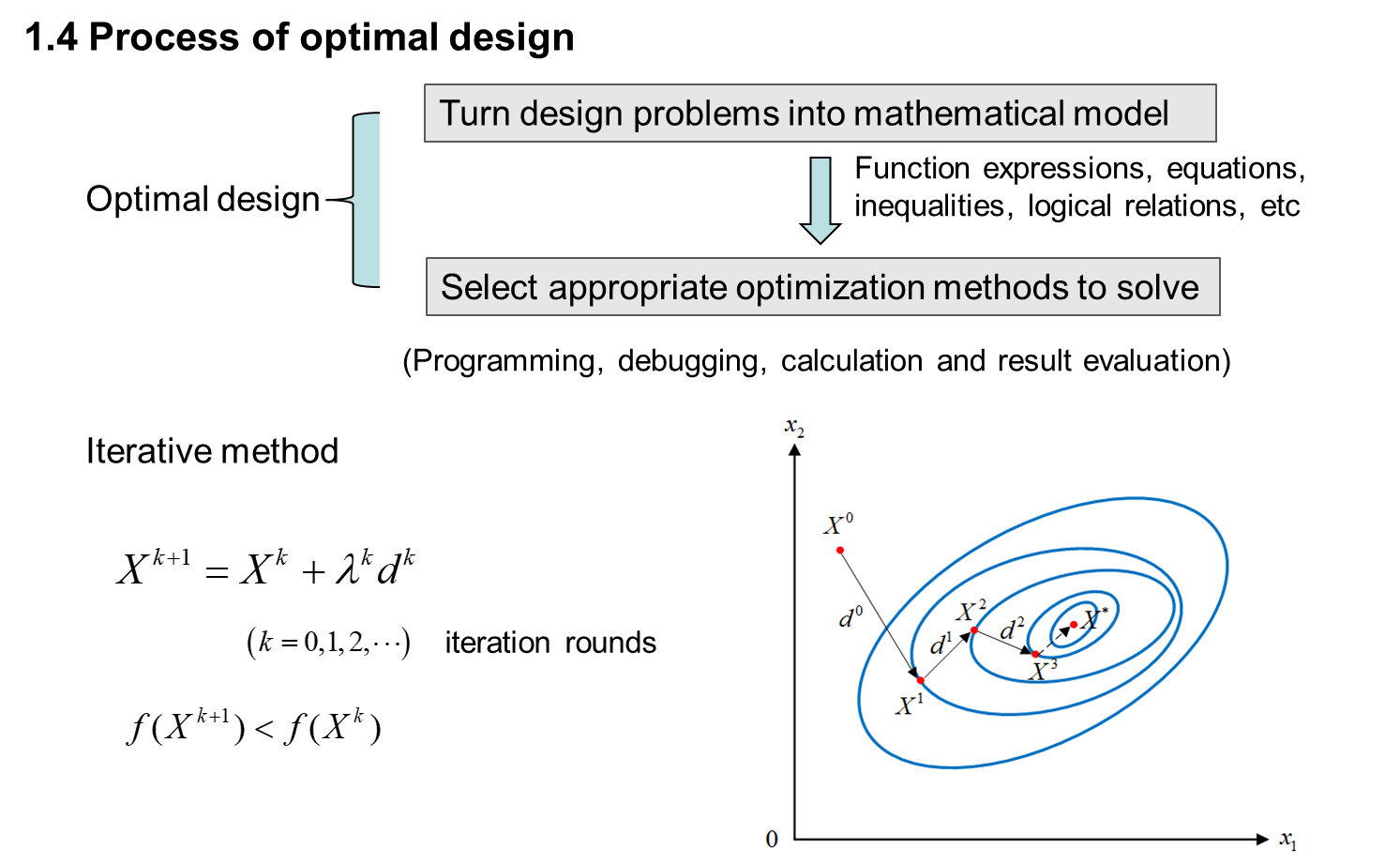

二、 MATLAB basis for optimization calculation

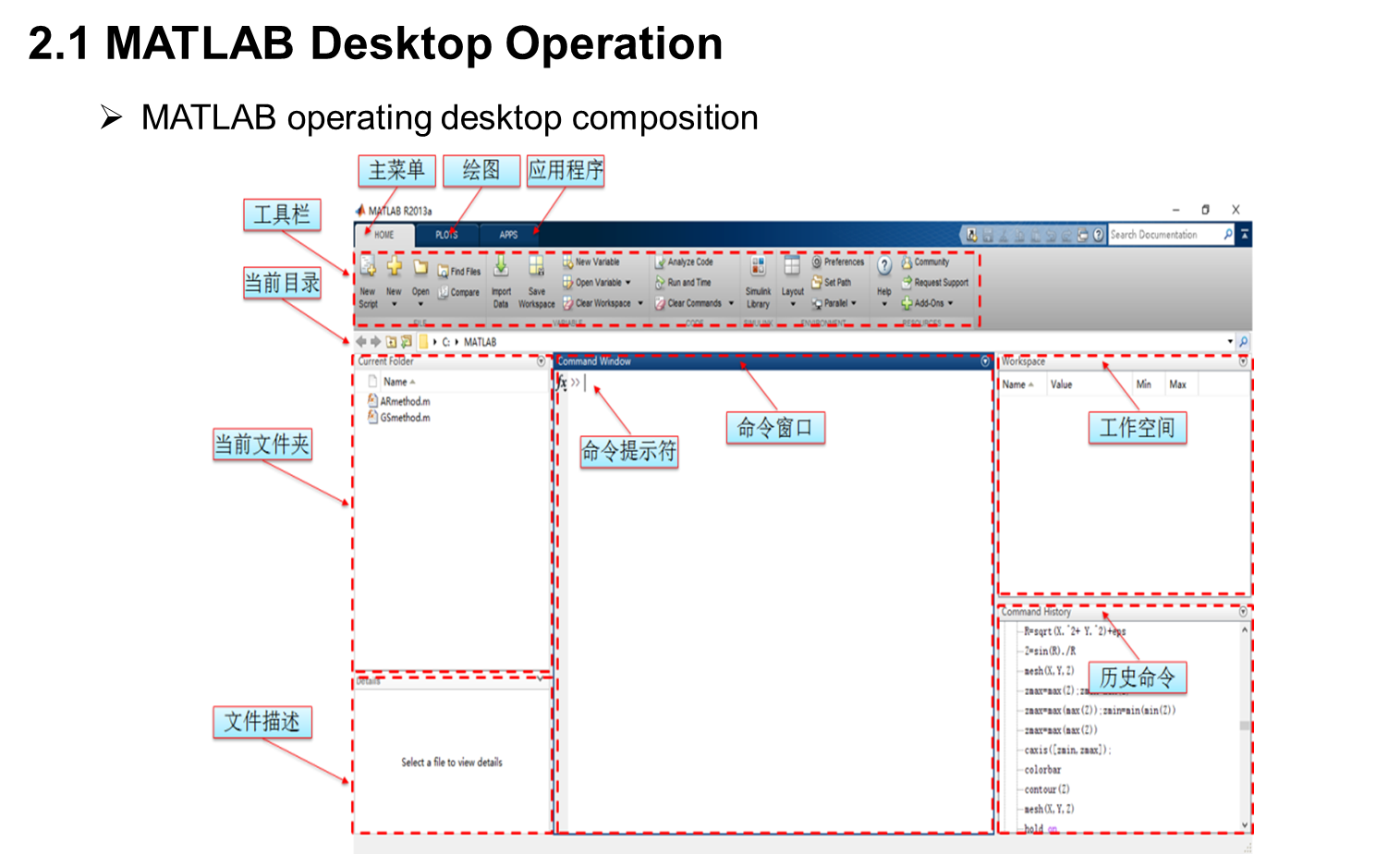

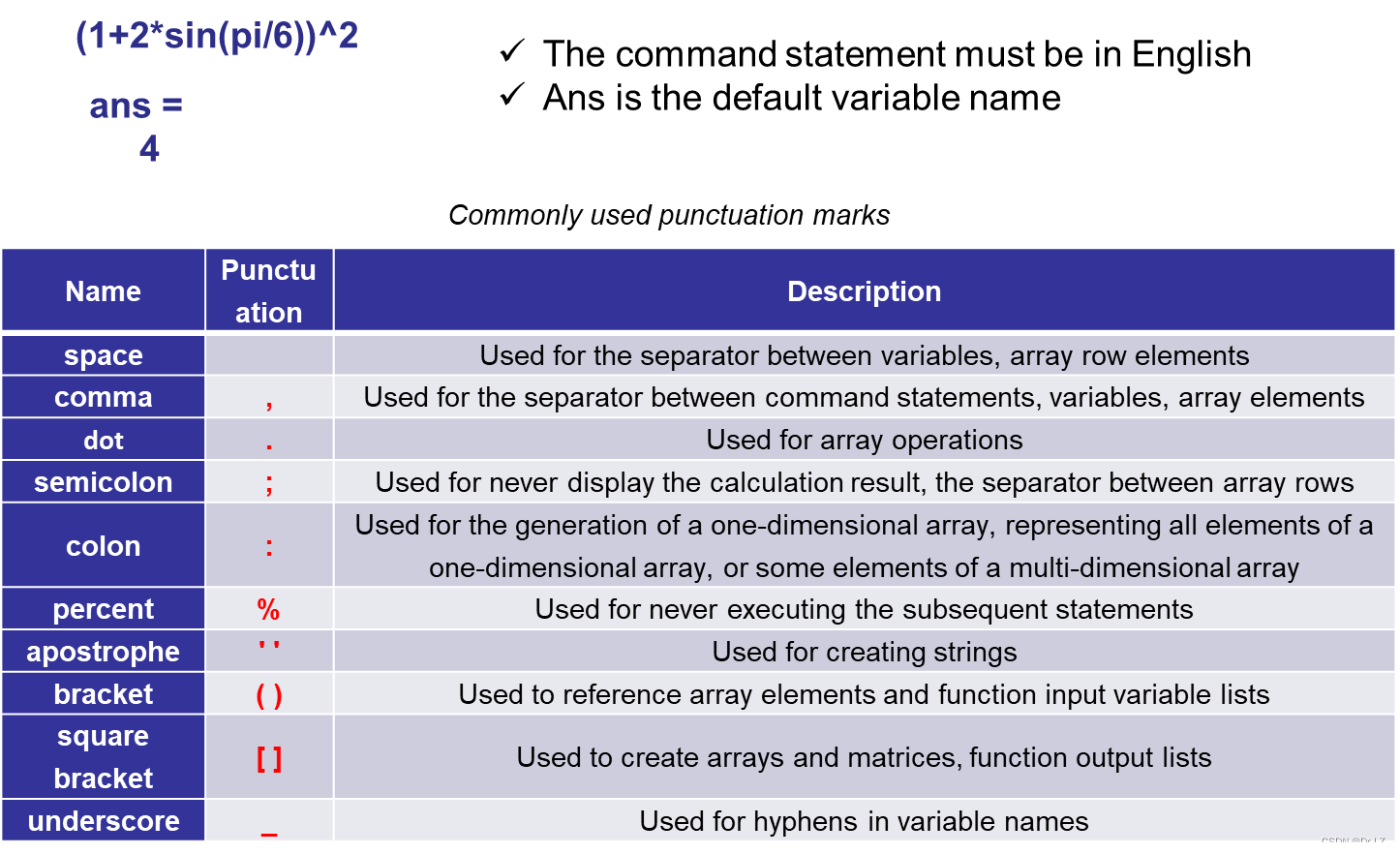

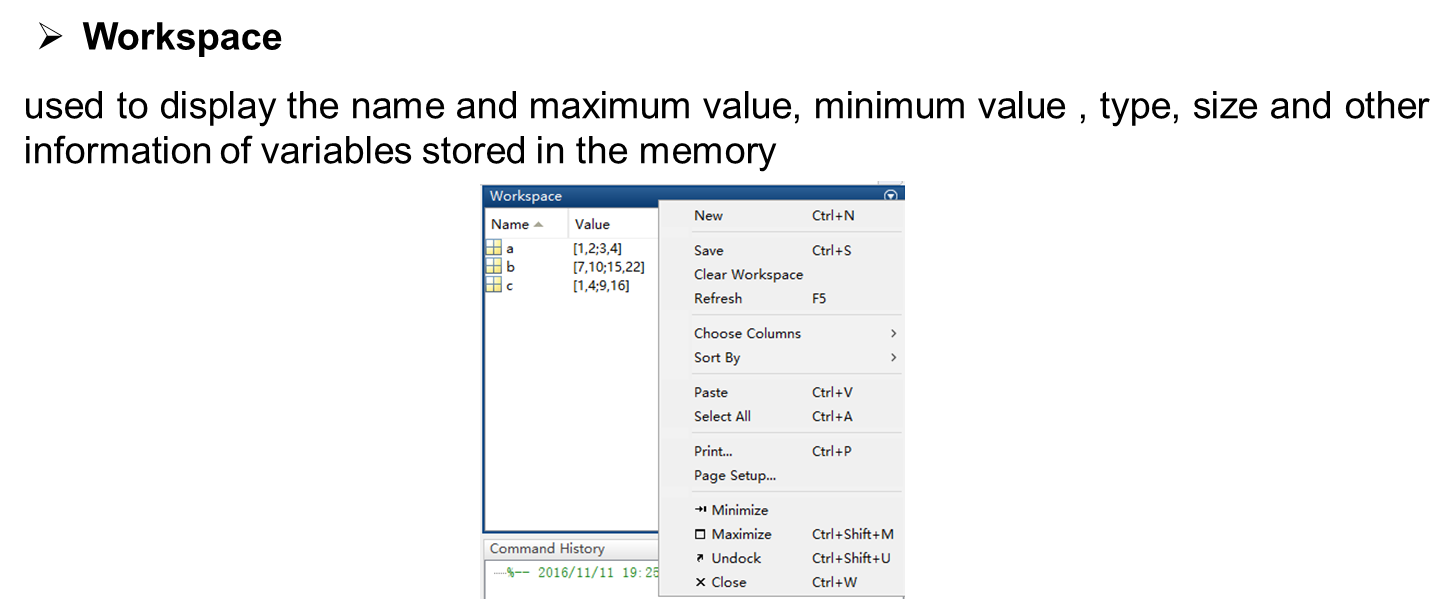
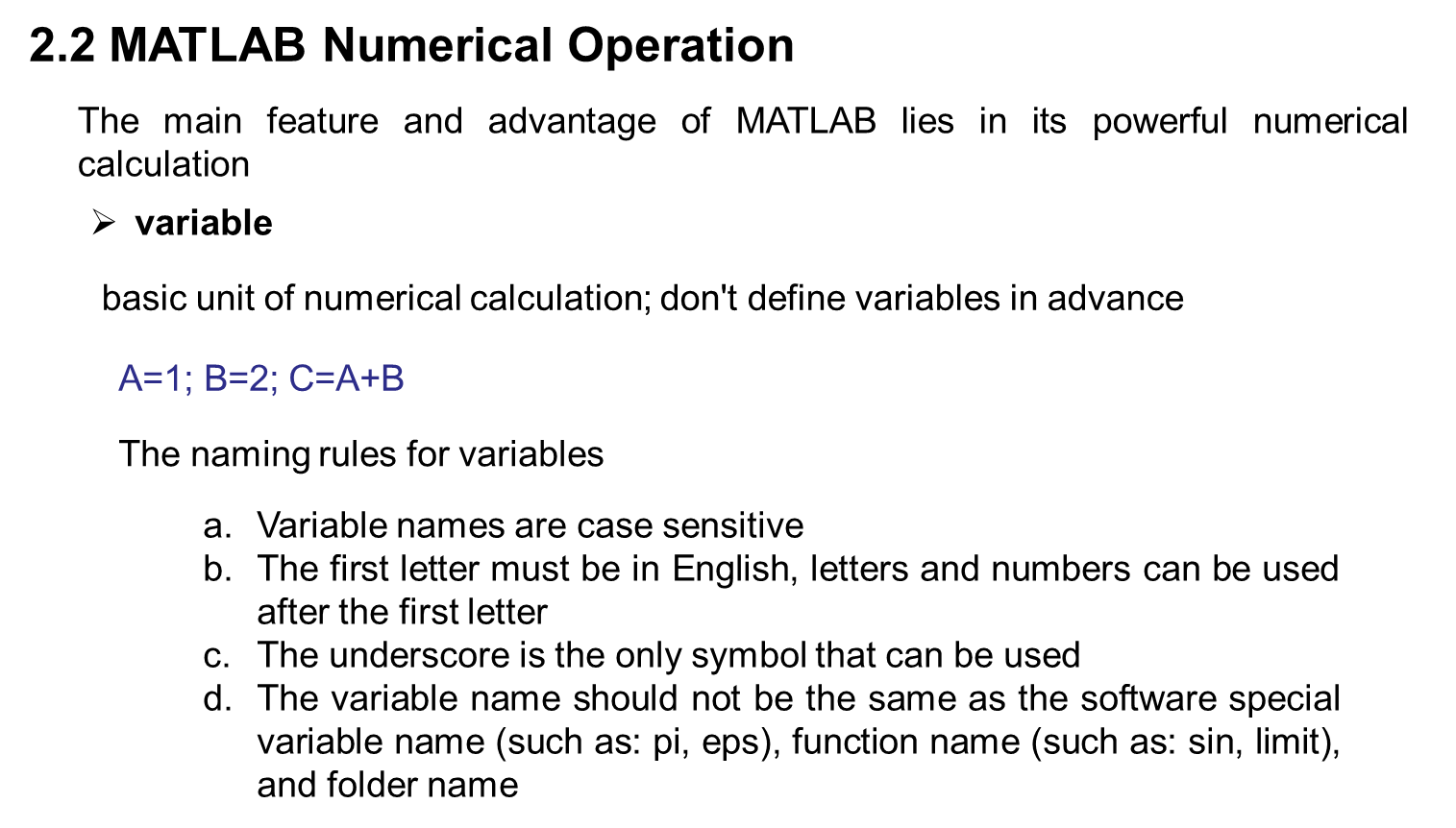

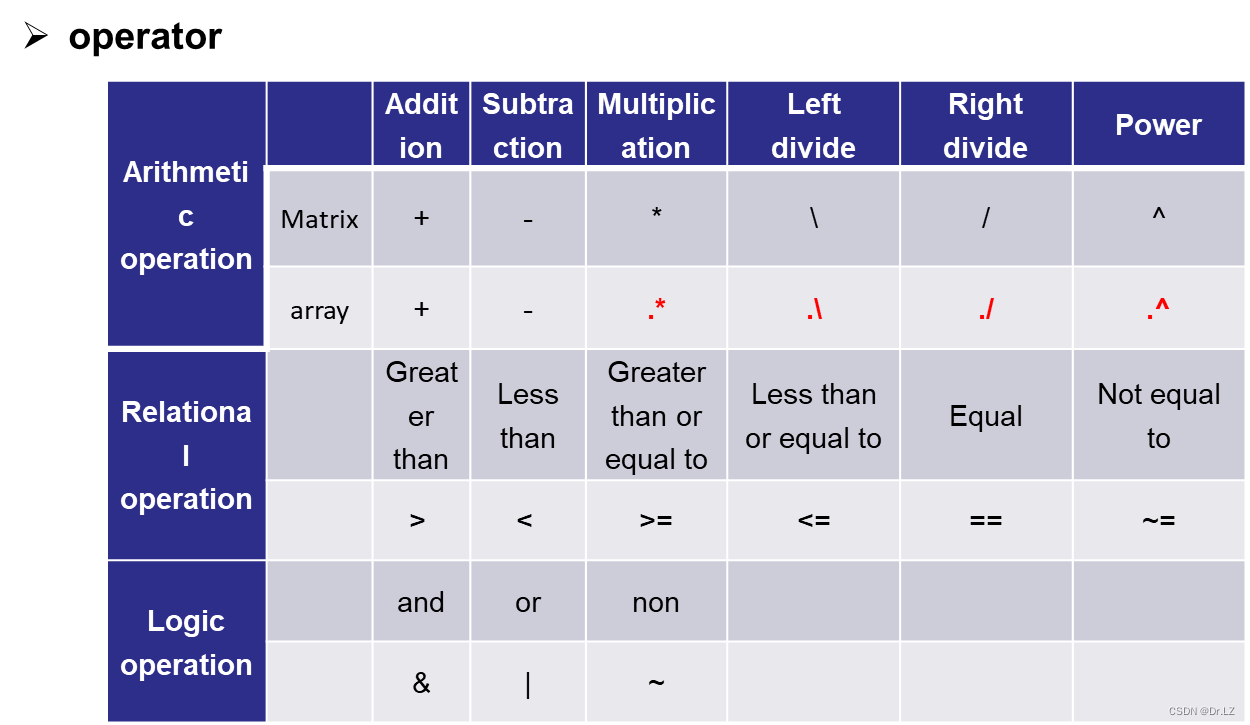


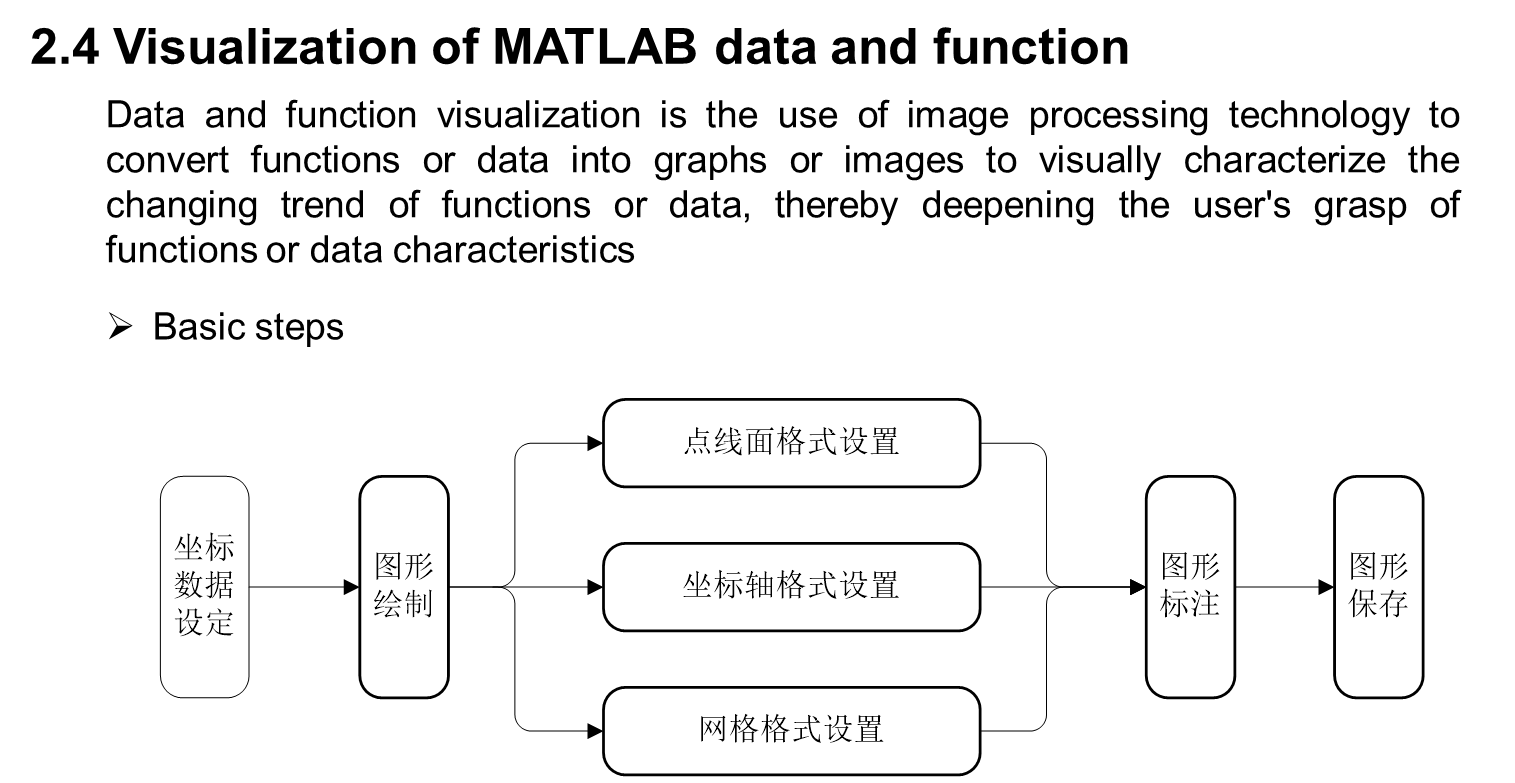
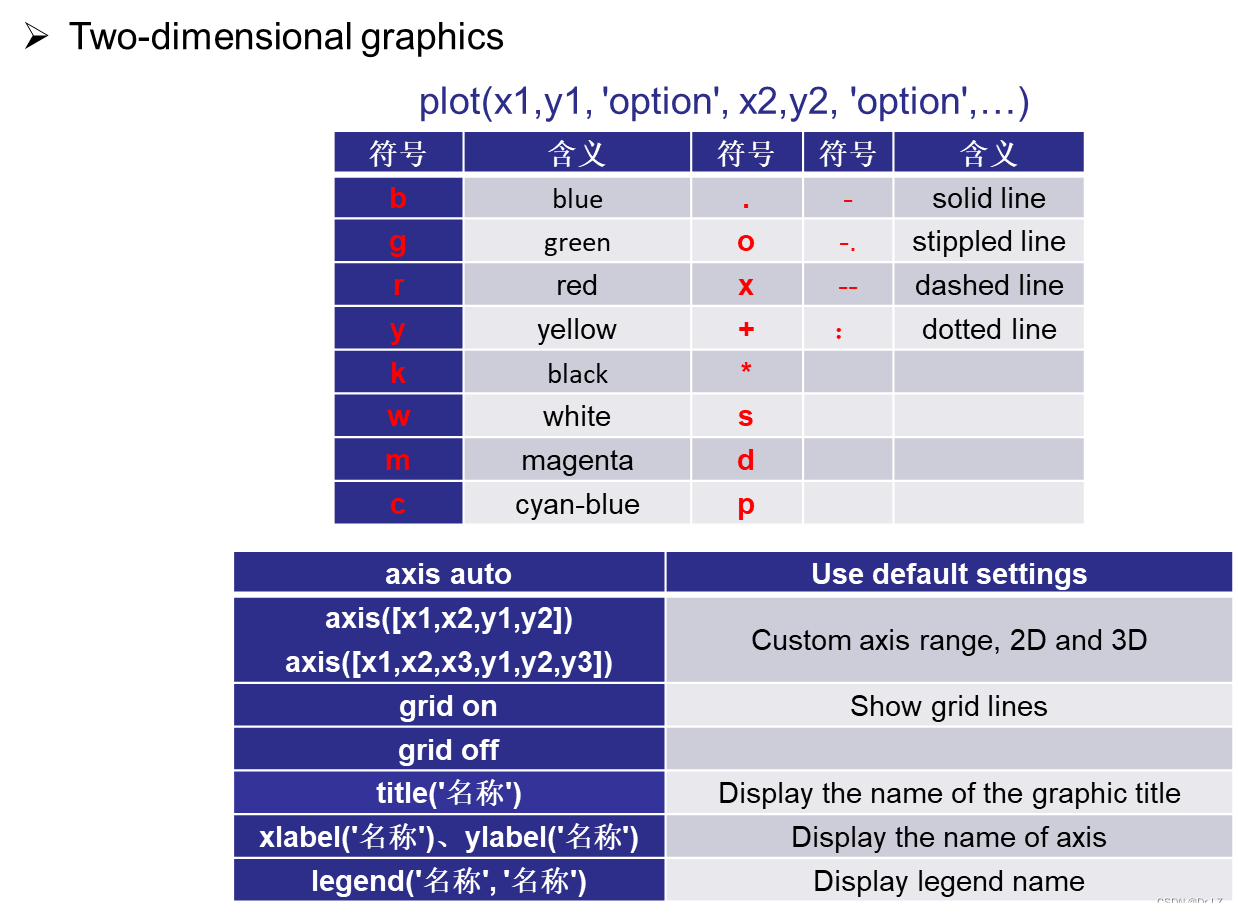
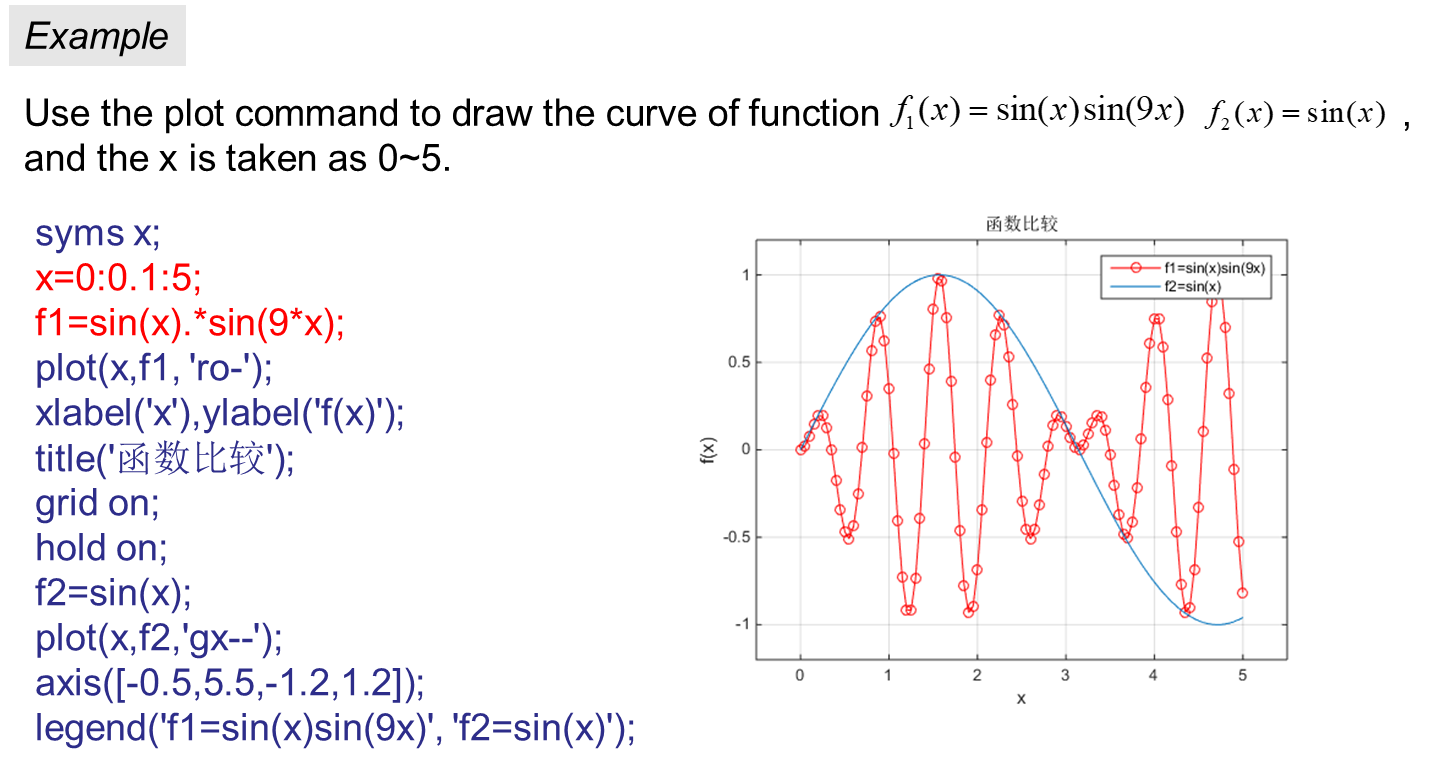
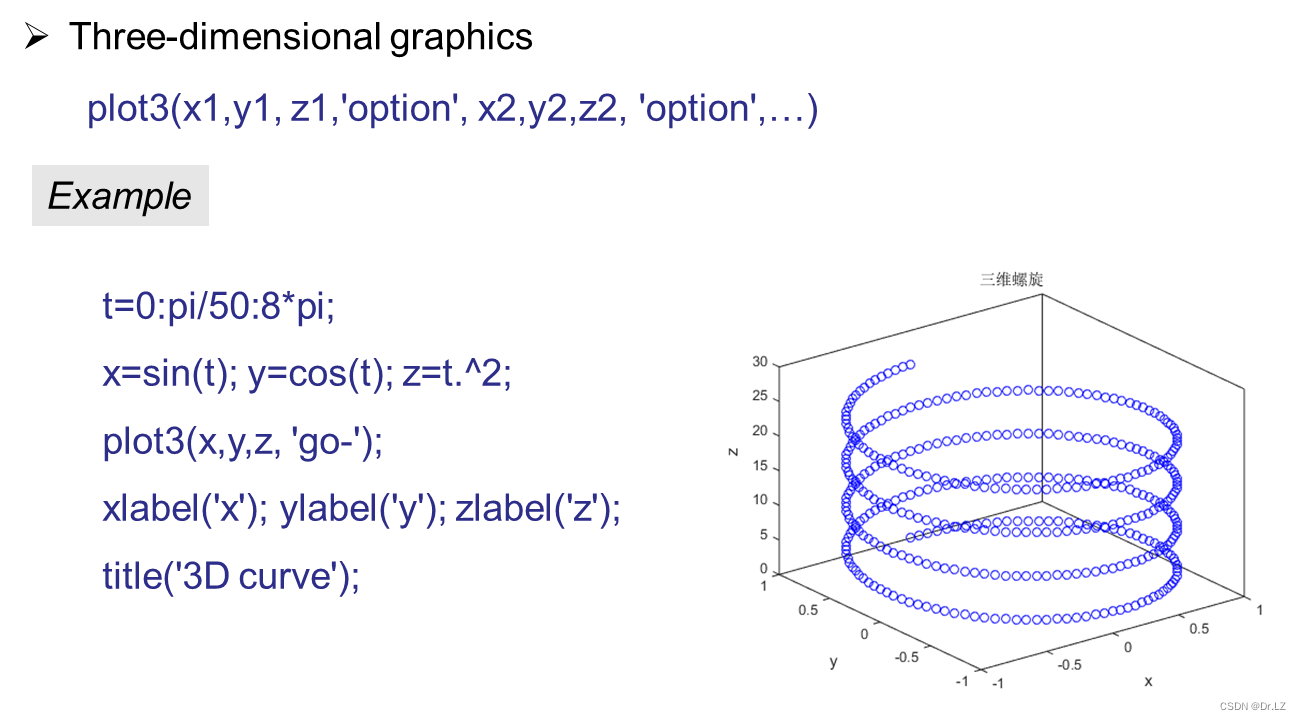
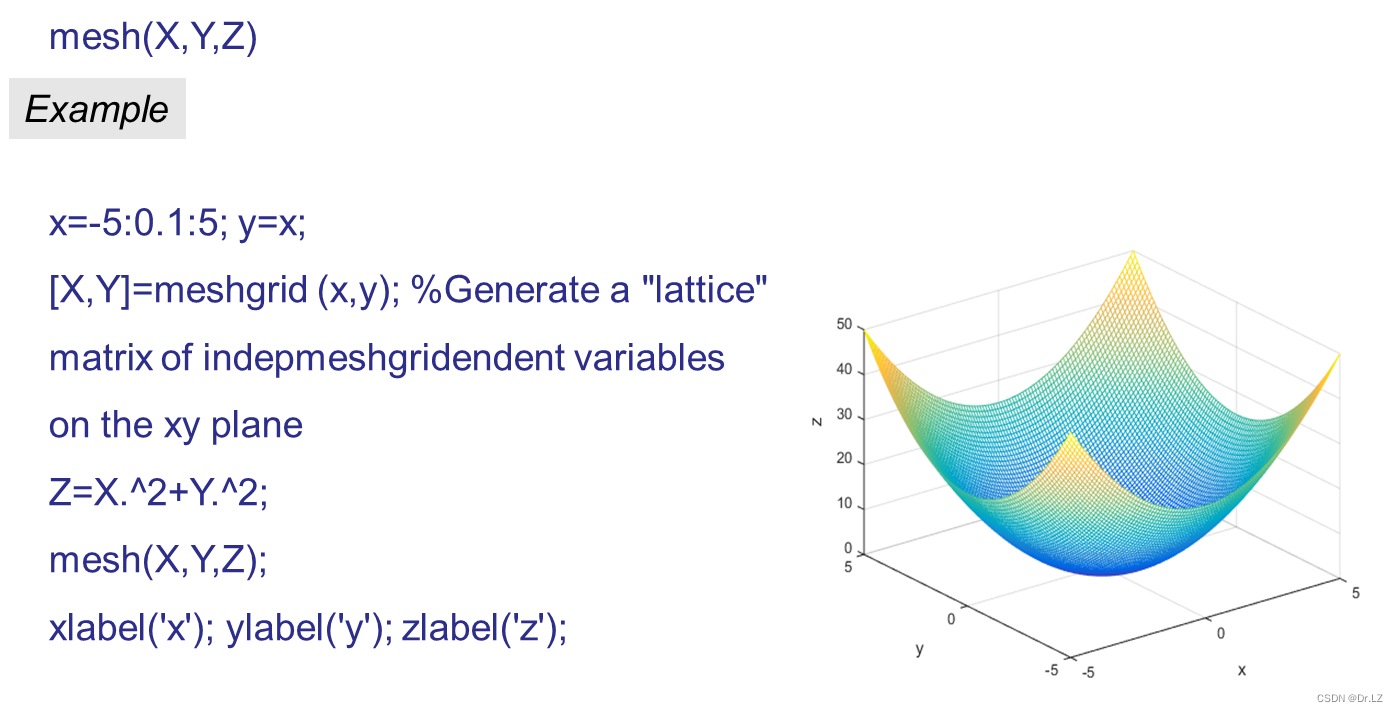
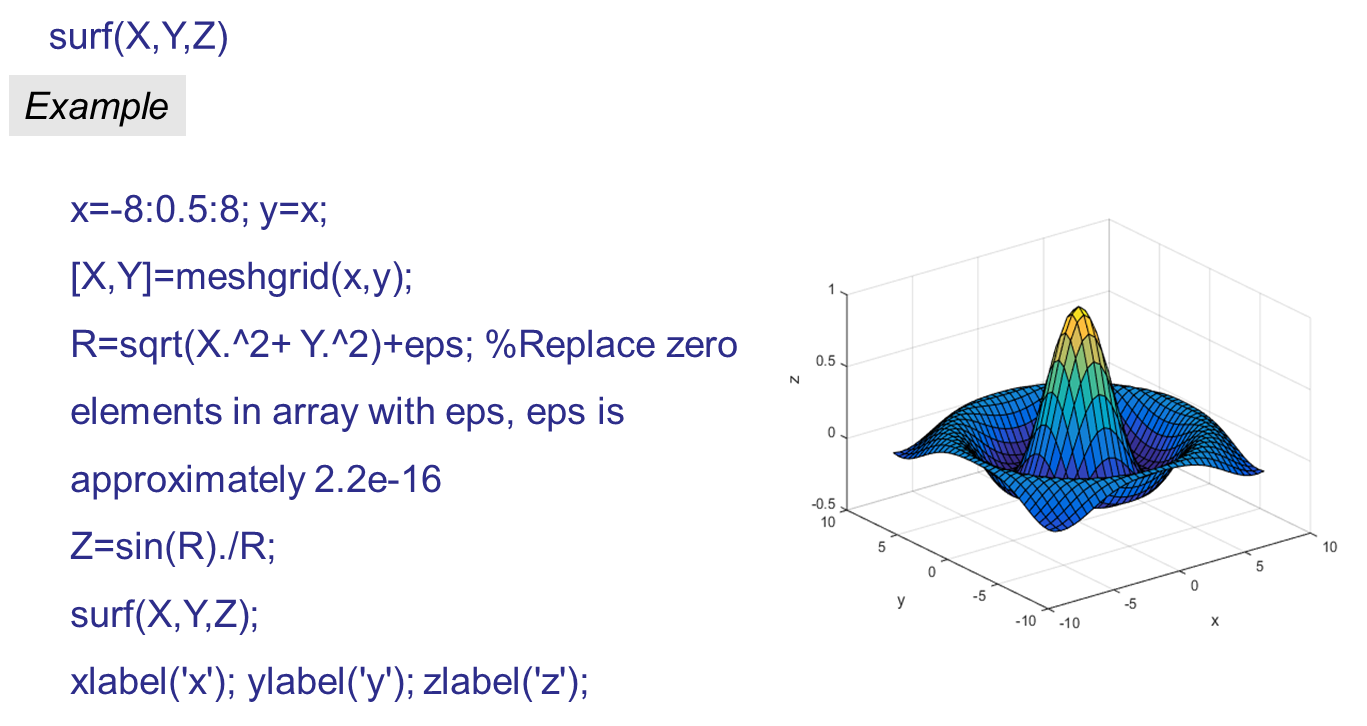











三、 Mathematical basis for optimization calculation

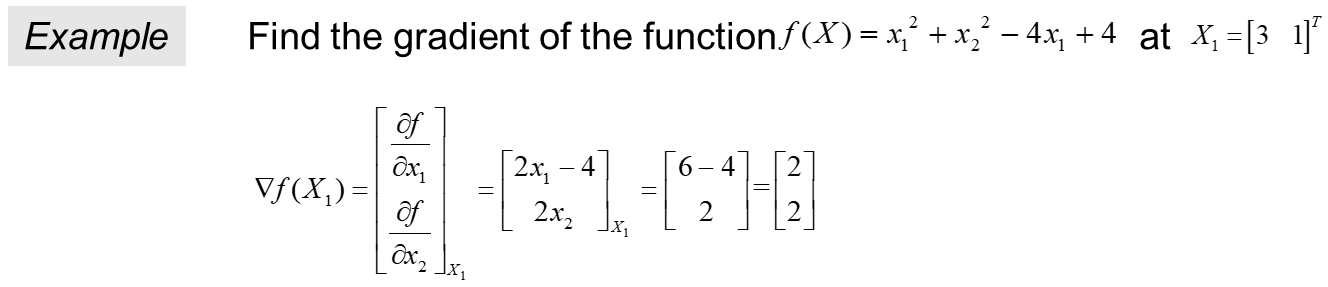
syms x1 x2 %定义符号变量x1 x2
var=[x1,x2]; %定义变量
fun=x1^2+x2^2-4*x1+4; %定义目标函数
disp('梯度表达式为:');
gra_exp=jacobian(fun,var).' %梯度表达式,列向量形式
X1=[3,1];
disp('X1点处梯度为:');
gra_val=subs(gra_exp,var,X1) %求点X1处的梯度值
eval () %符号变量转为数值变量
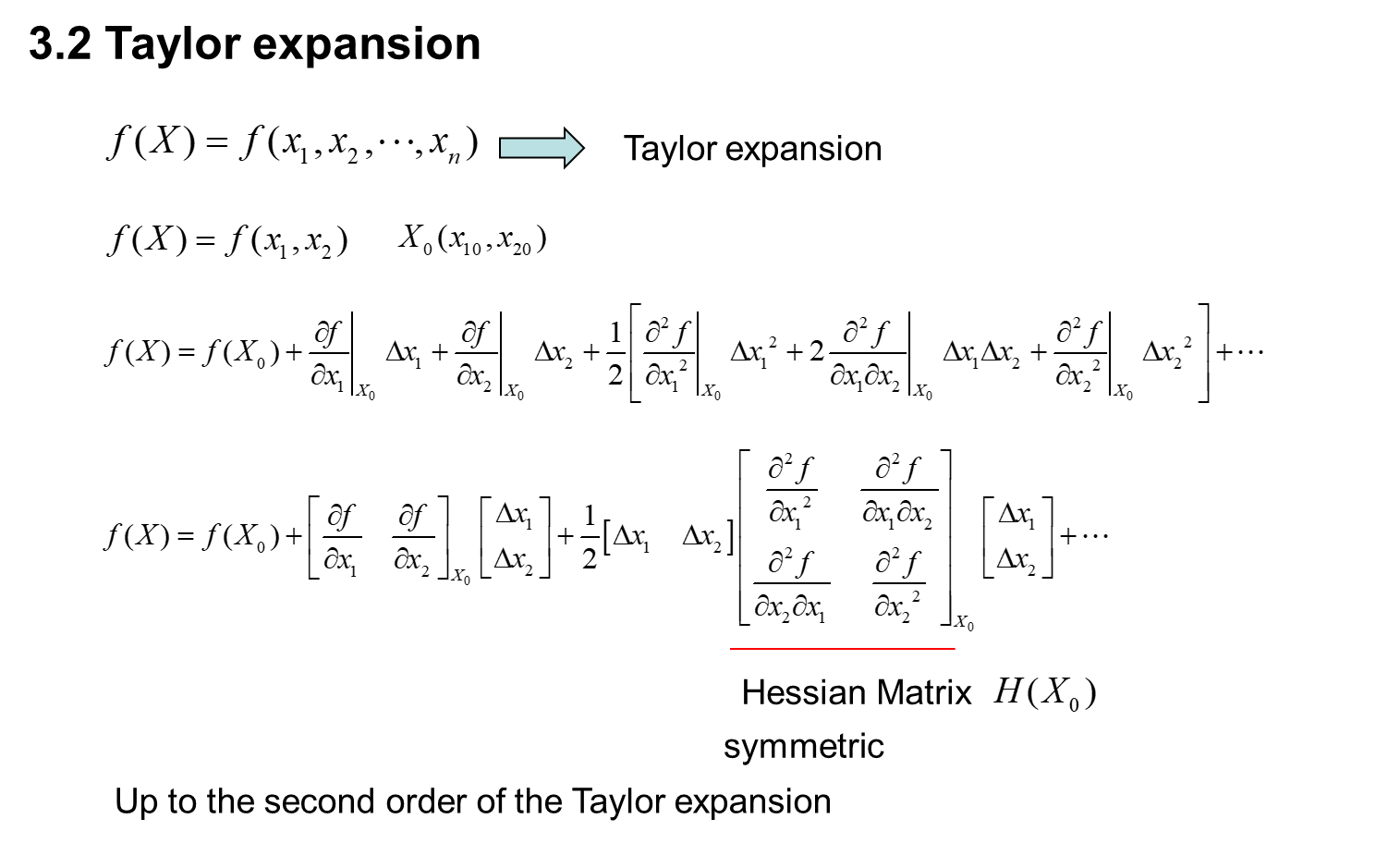
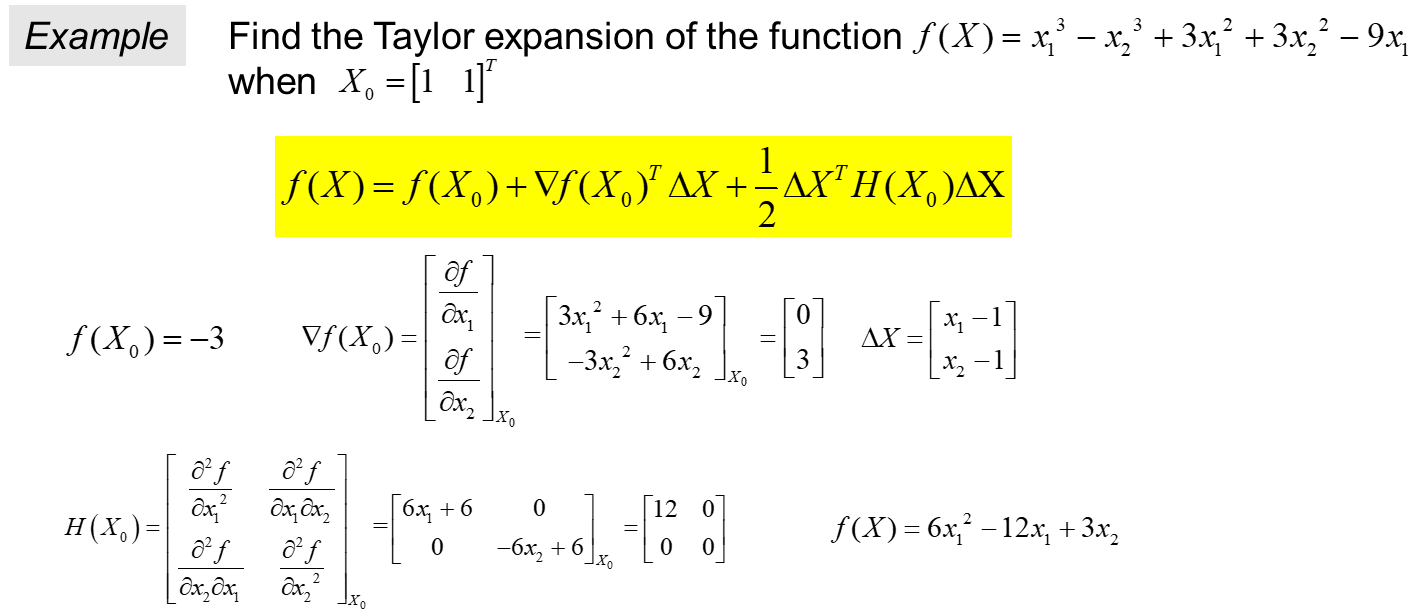
syms x1 x2
var=[x1,x2];
fun=x1^3-x2^3+3*x1^2+3*x2^2-9*x1;
disp('函数的二阶泰勒展开式为:');
taylor(fun,var,[1,1],'order',3) %求函数fun在点(1,1)处的二阶泰勒展开式
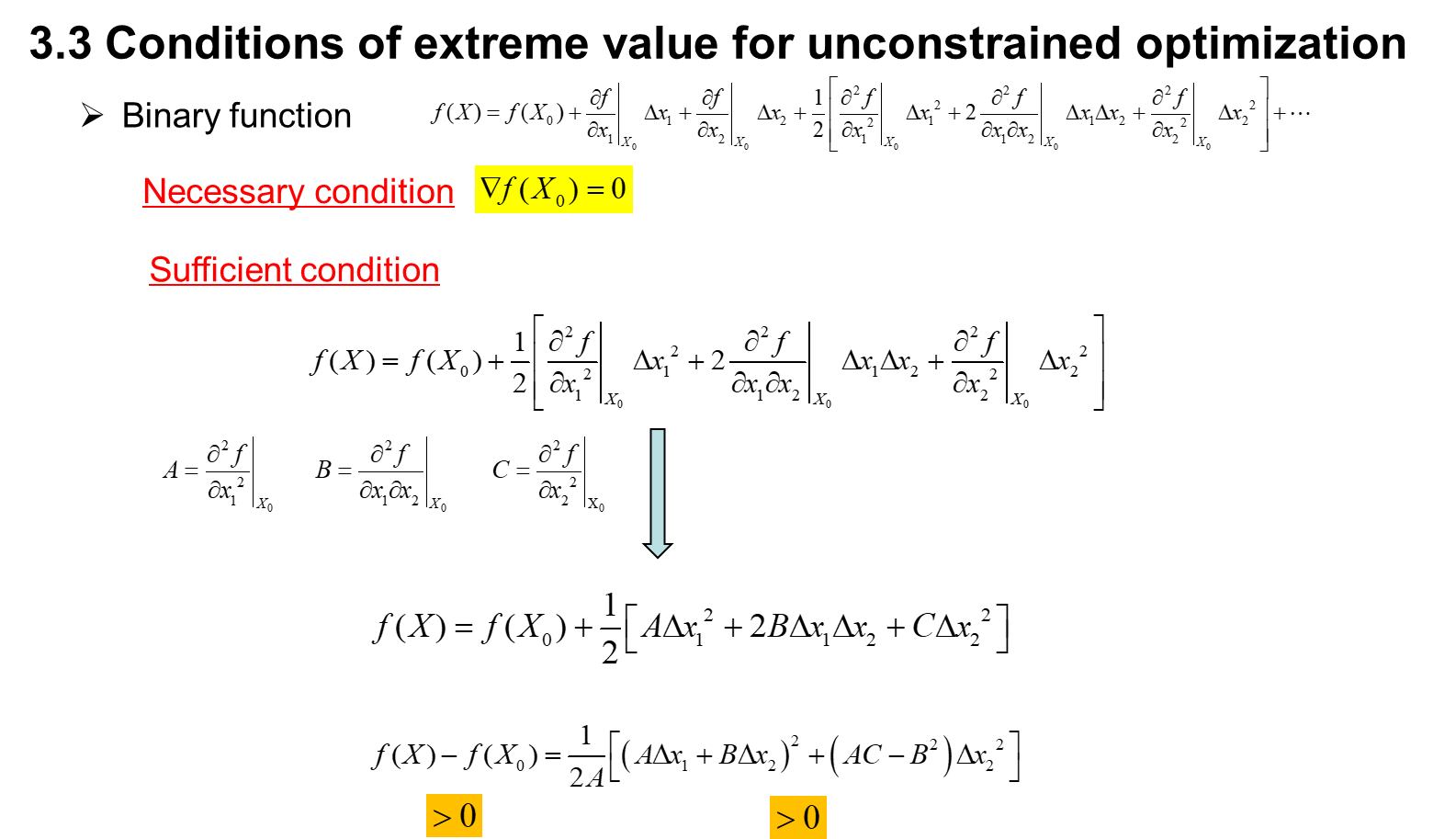


syms x1 x2
var=[x1,x2];
fun=x1^3+x2^3-3*x1-3*x2^2;
gra_exp=jacobian(fun,var).'; %梯度表达式,列向量形式
H_exp=jacobian(gra_exp,var); %海塞矩阵表达式
dx1=gra_exp(1,1);
dx2=gra_exp(2,1);
[x,y]=solve(dx1,dx2,x1,x2); %求梯度为0对应的点
disp('梯度为零的点为:');
X=[x,y]
for i=1:4
H_val=subs(H_exp,var,X(i,:))
[D,p]=chol(H_val)
if p==0
disp('极小值点为:')
X_opti= X(i,:)
disp('函数极小值为:')
minf=subs(fun,var,X(i,:))
break
end
end
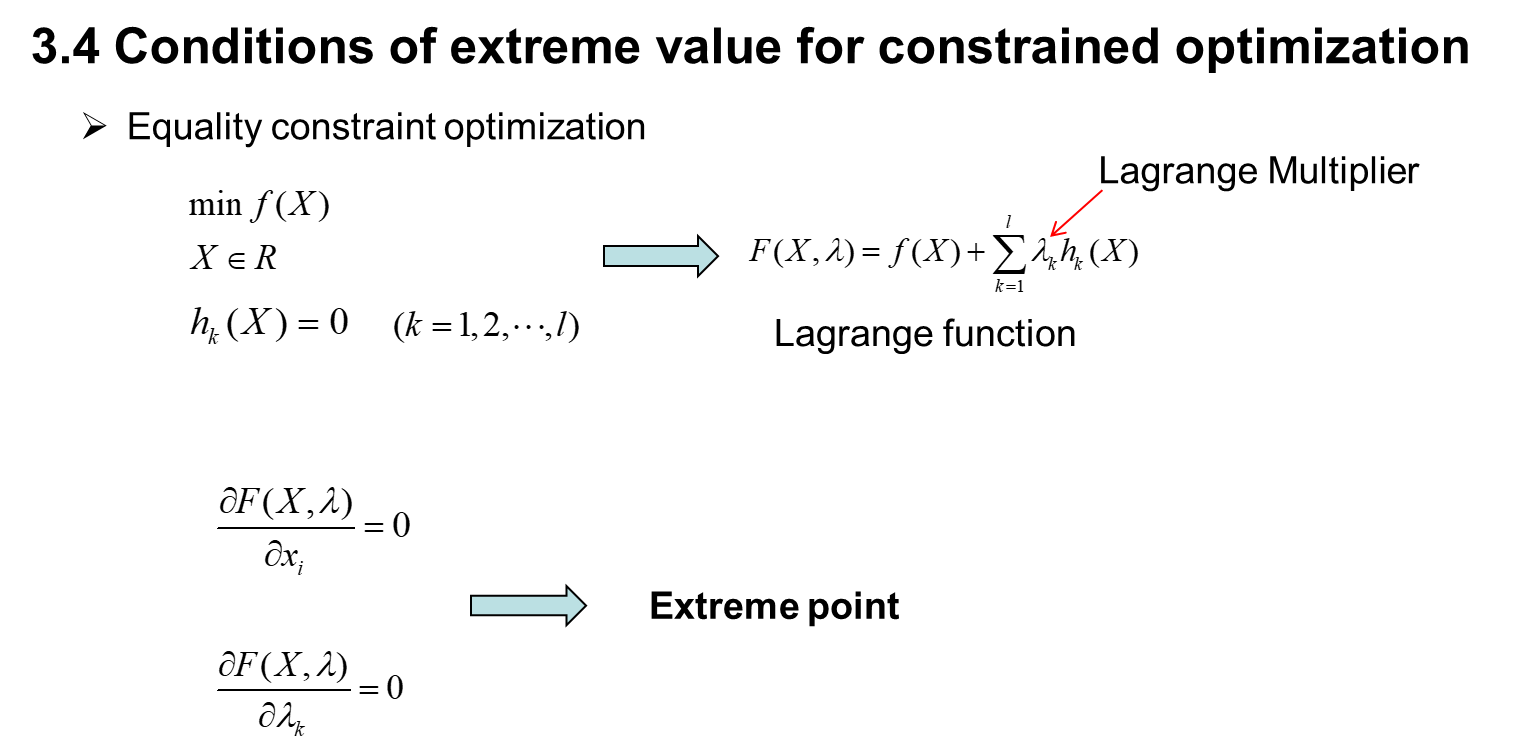

syms x1 x2 lam
var=[x1,x2,lam];
fun=x1^2+x2^2-4;
h=x1-x2+2;
Fun=fun+lam*h;
gra_exp=jacobian(Fun,var).'; %梯度表达式,列向量形式
dx1=gra_exp(1,1);
dx2=gra_exp(2,1);
dlam=gra_exp(3,1);
[x1,x2,lam]=solve(dx1,dx2,dlam,x1,x2,lam); %求梯度为0的点
disp('极值点坐标为:');
X_opti=[x1,x2]

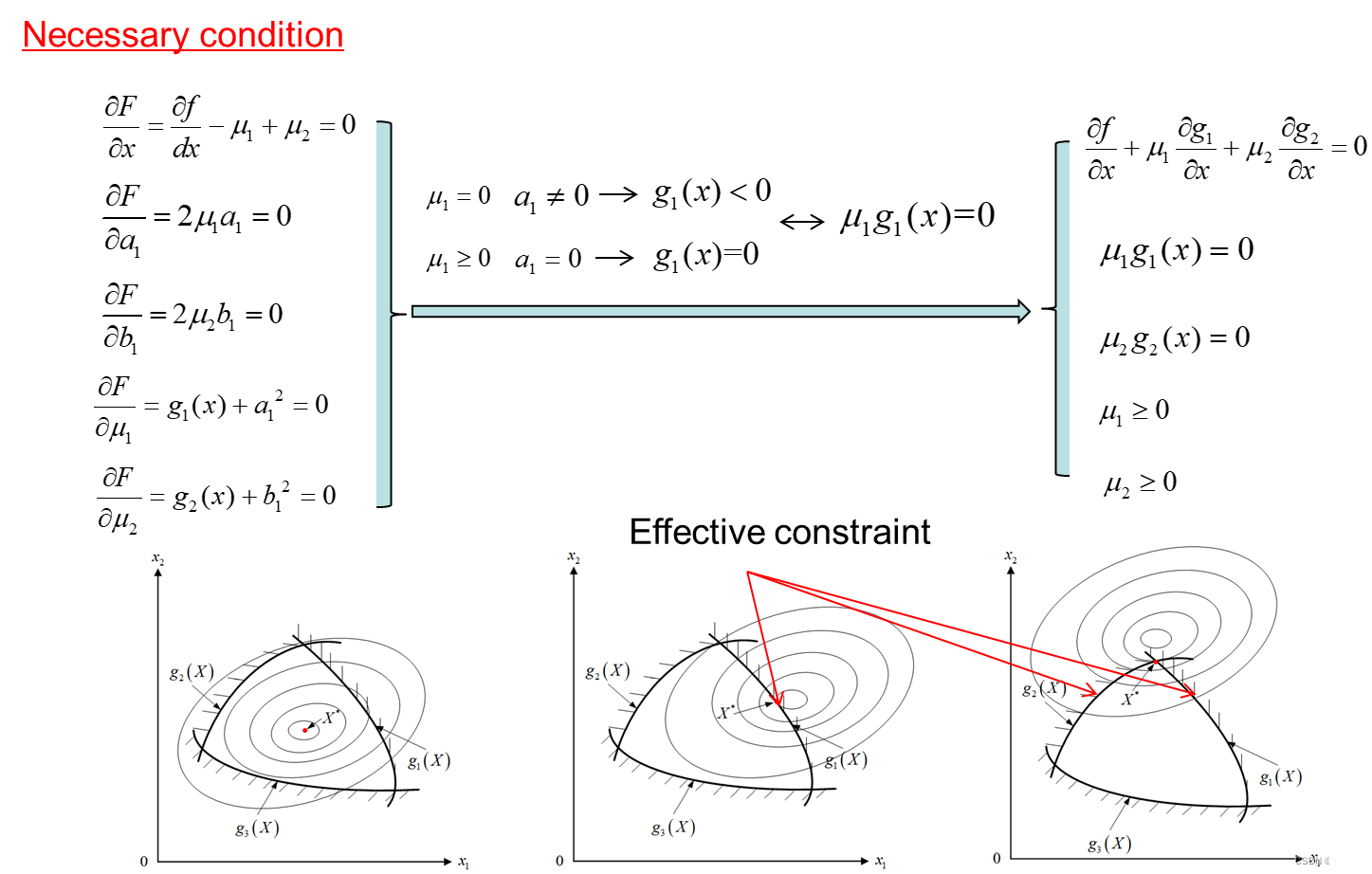
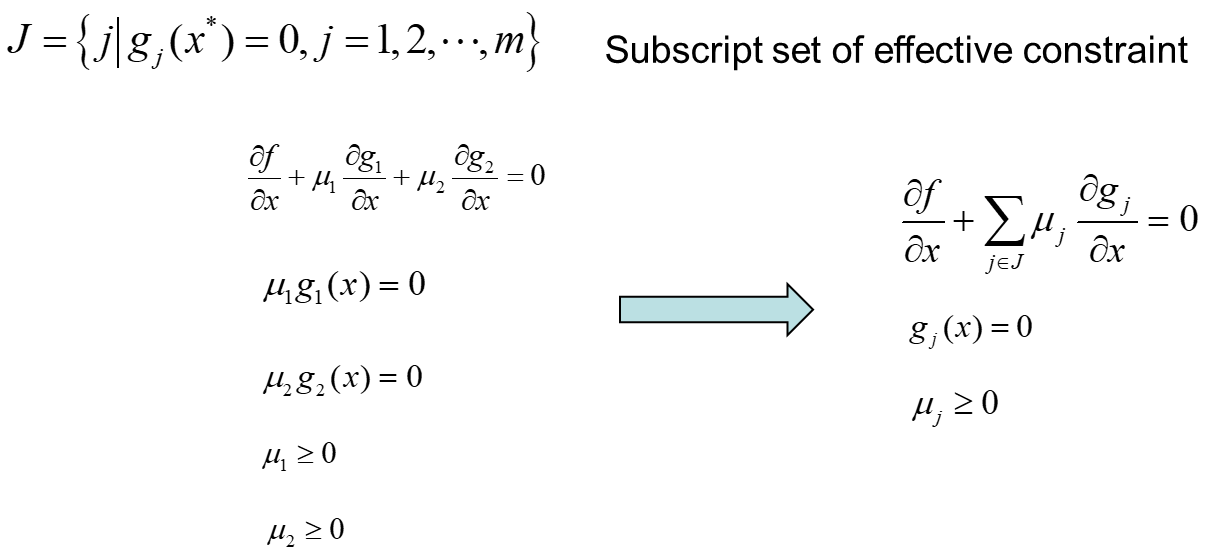
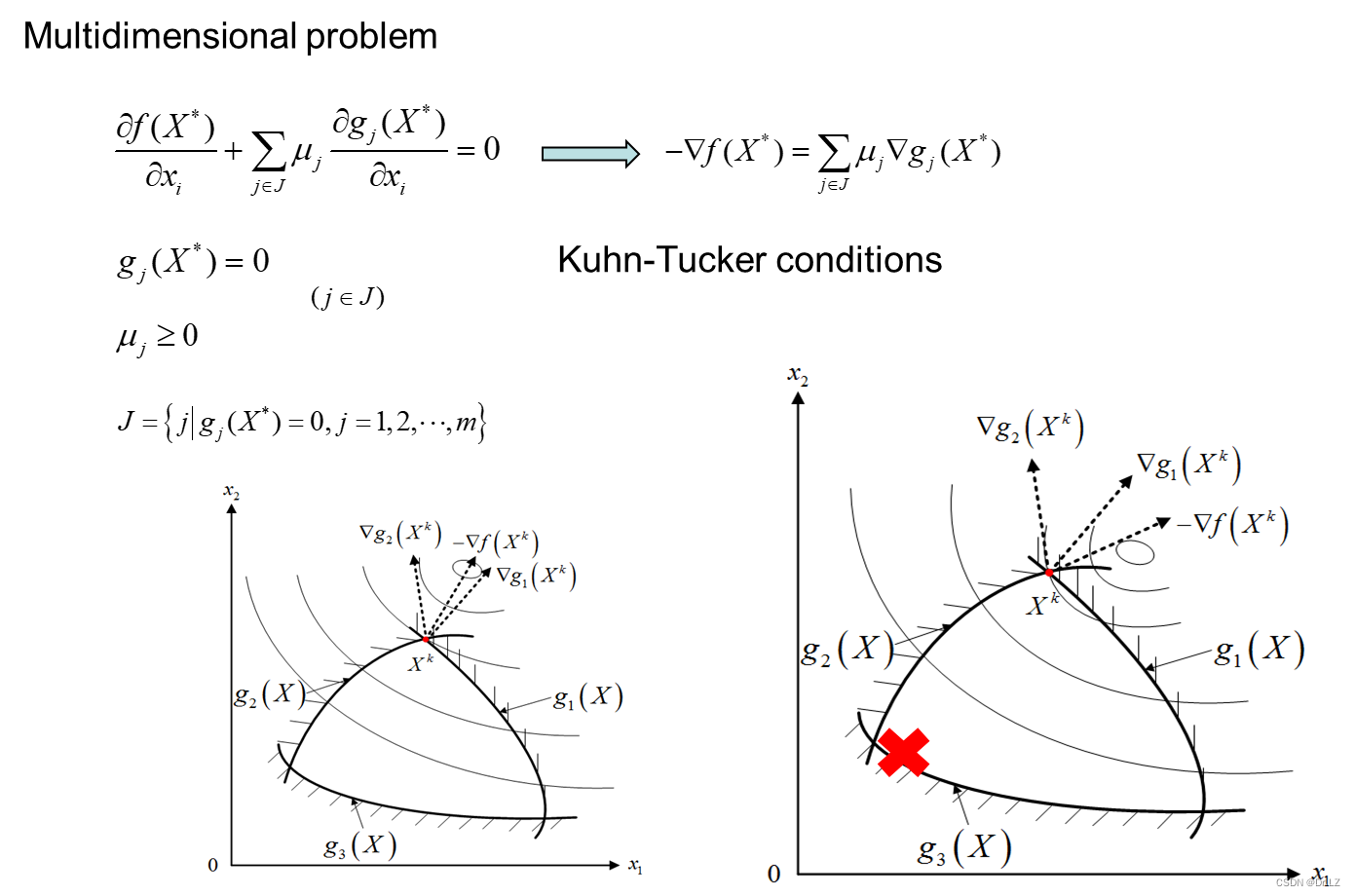
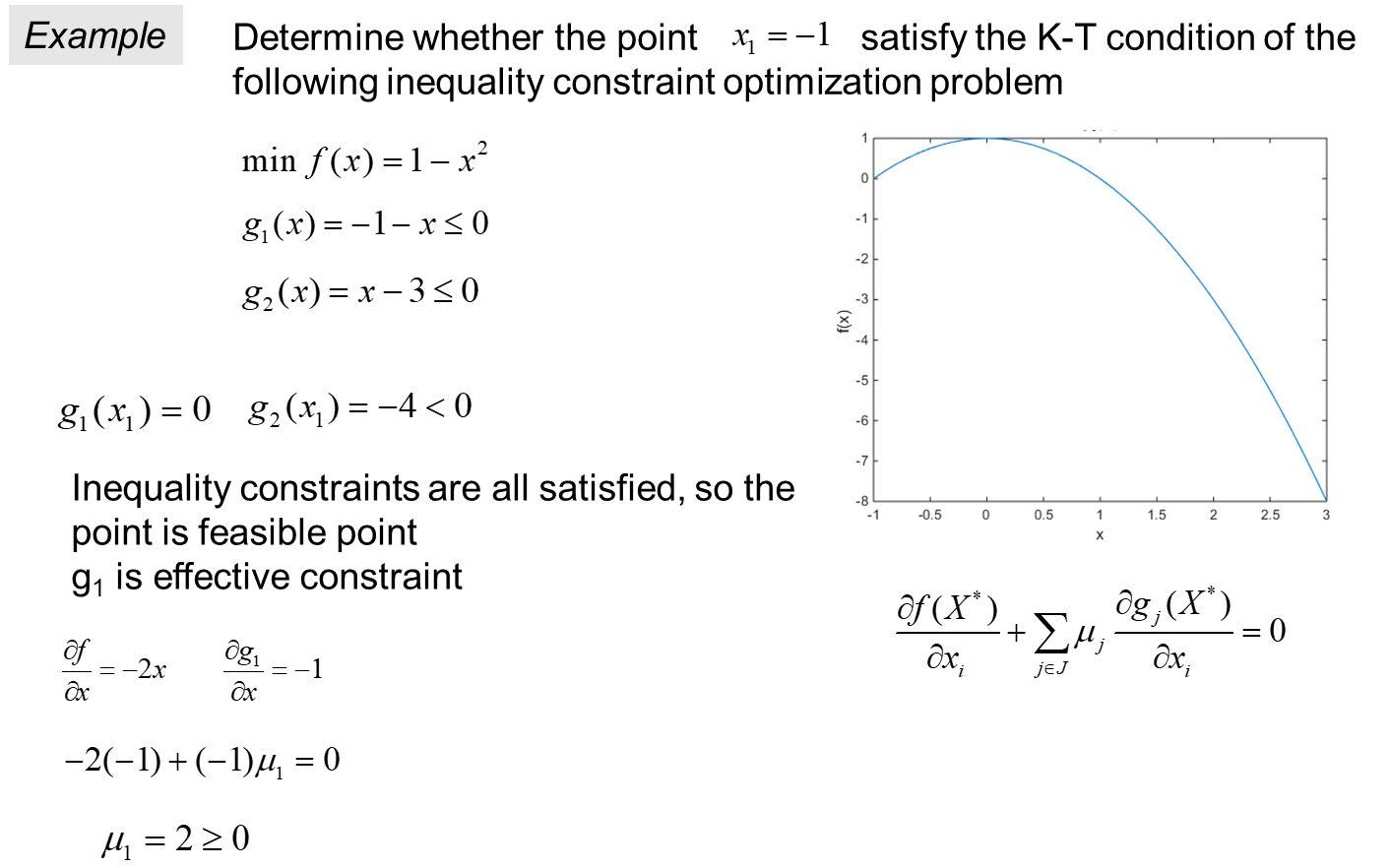

四、 One-dimensional optimization

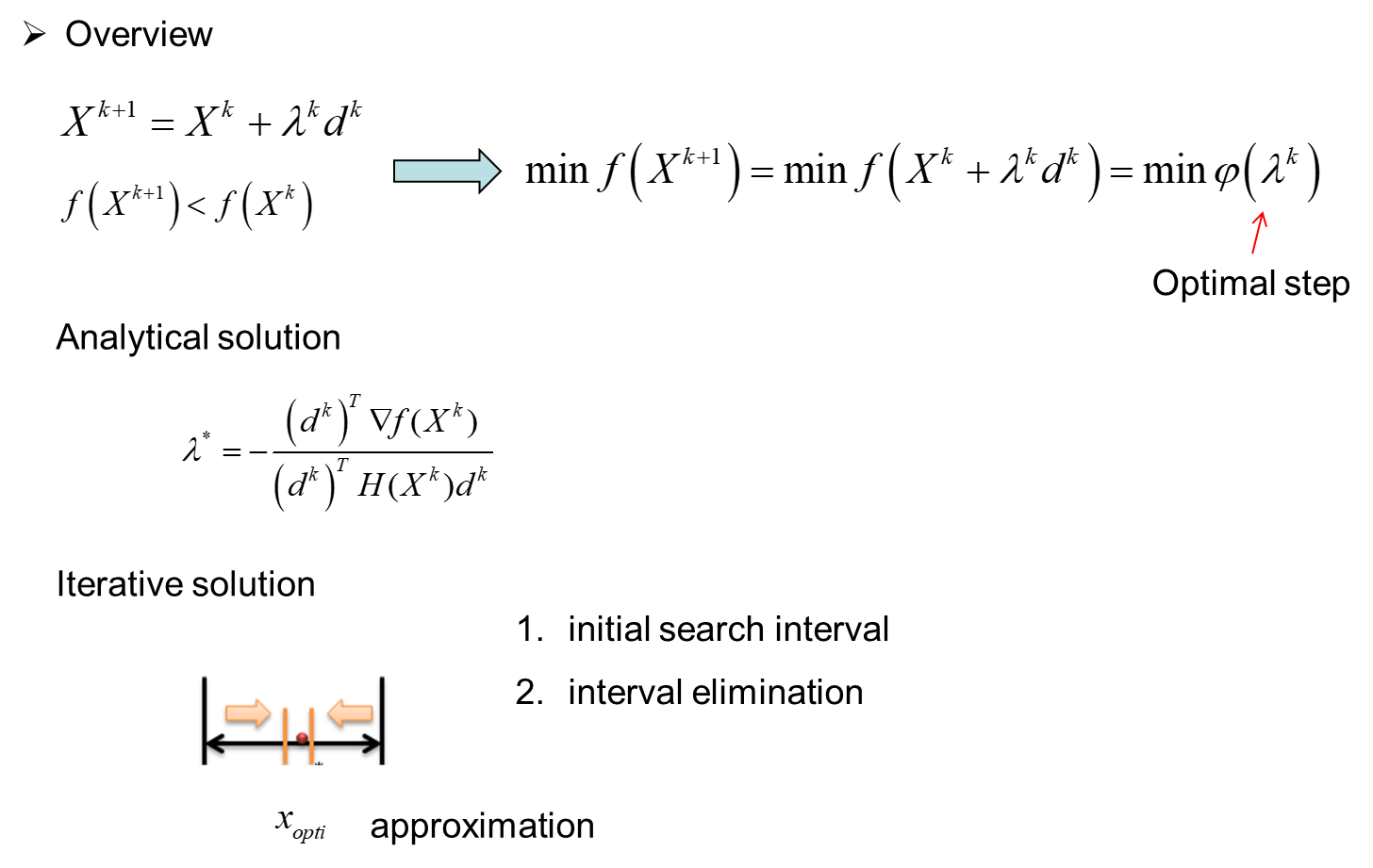
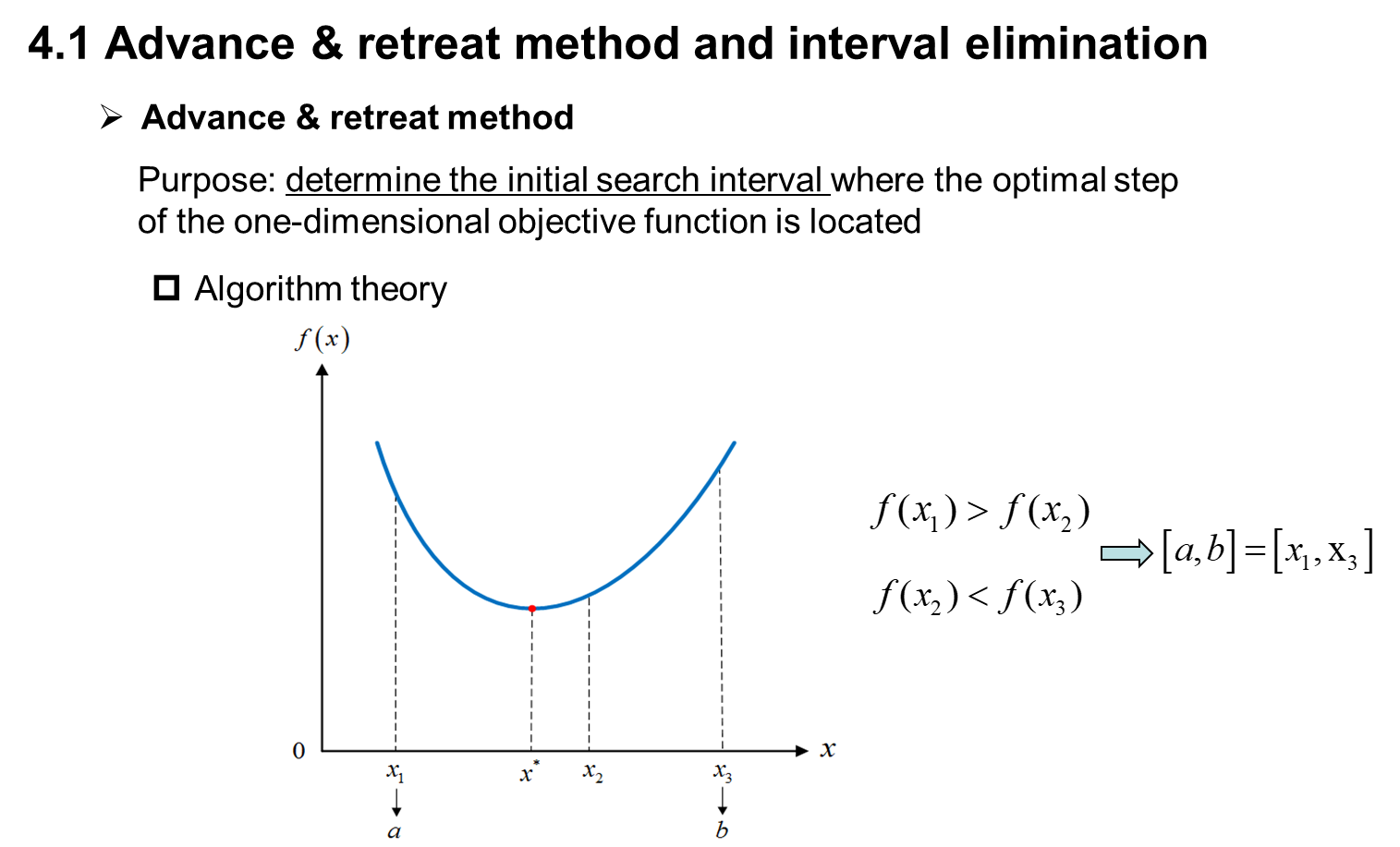
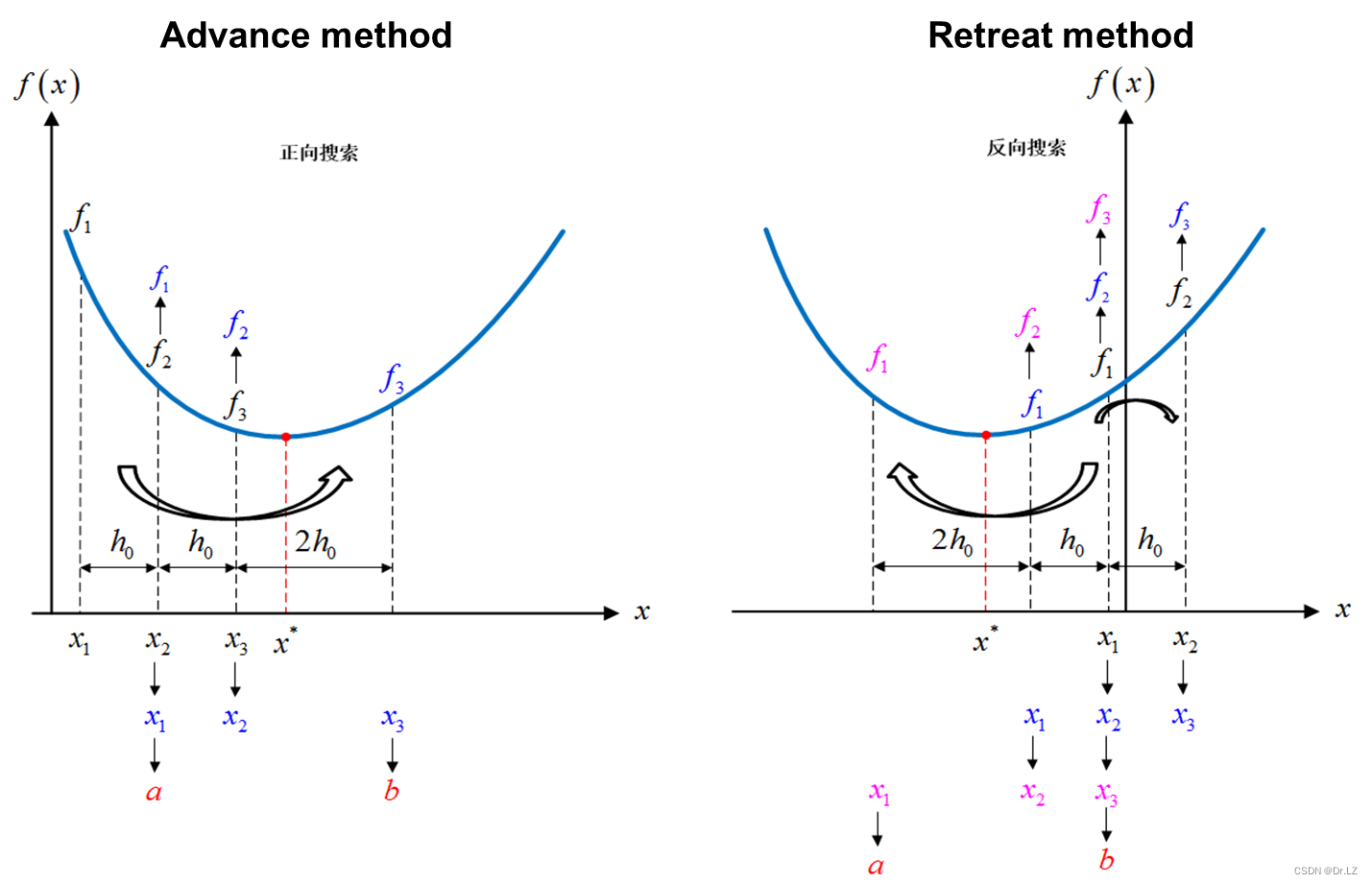
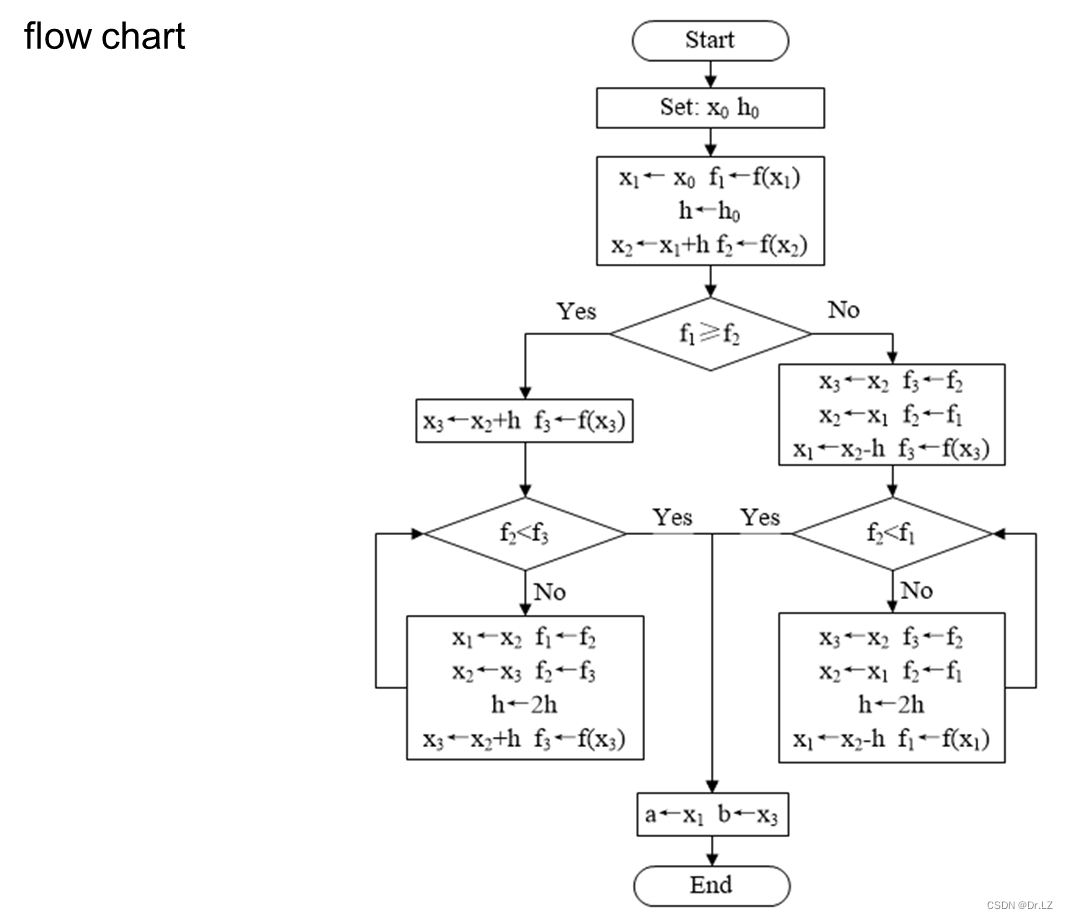
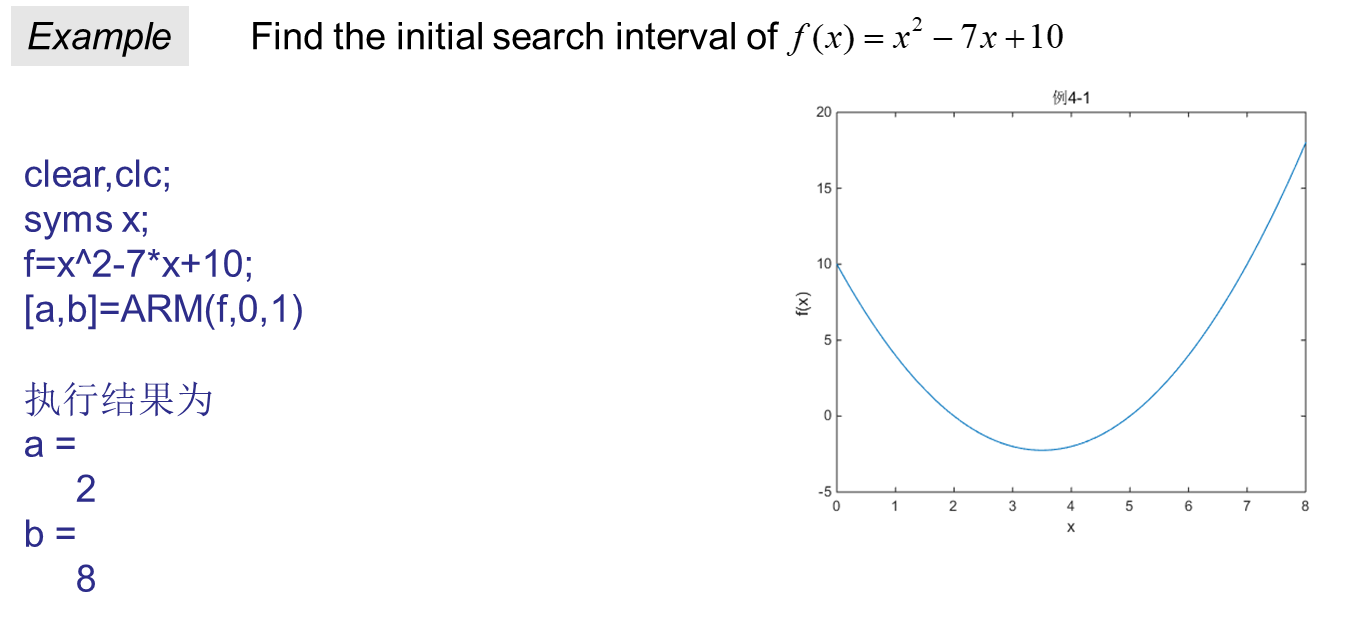
function[a,b]=ARM(f,x0,h0)
%ARM.m Advance&Retreat Method(进退法:求一维搜索的初始搜索区间),函数调用格式为[a,b]=ARM(f,x0,h0)
%a:初始搜索区间的下限(输出)
%b:初始搜索区间的上限(输出)
%f:一维目标函数(输入)
%x0:初始点(输入)
%h0:初始步长(输入)
x1=x0;
f1=eval(subs(f,findsym(f),x1));
h=h0;
x2=x1+h;
f2=eval(subs(f,findsym(f),x2));
if f1>=f2
while 1 %1为真
x3=x2+h;
f3=eval(subs(f,findsym(f),x3));
if f2>f3
x1=x2;
x2=x3;
f2=f3;
h=2*h;
else
a=x1;
b=x3;
break;
end
end
else %反向搜索
x3=x2;
x2=x1;
f2=f1;
while 1
x1=x2-h;
f1=eval(subs(f,findsym(f),x1));
if f2>f1
x3=x2;
x2=x1;
f2=f1;
h=2*h;
else
a=x1;
b=x3;
break;
end
end
end
format compact,format short;
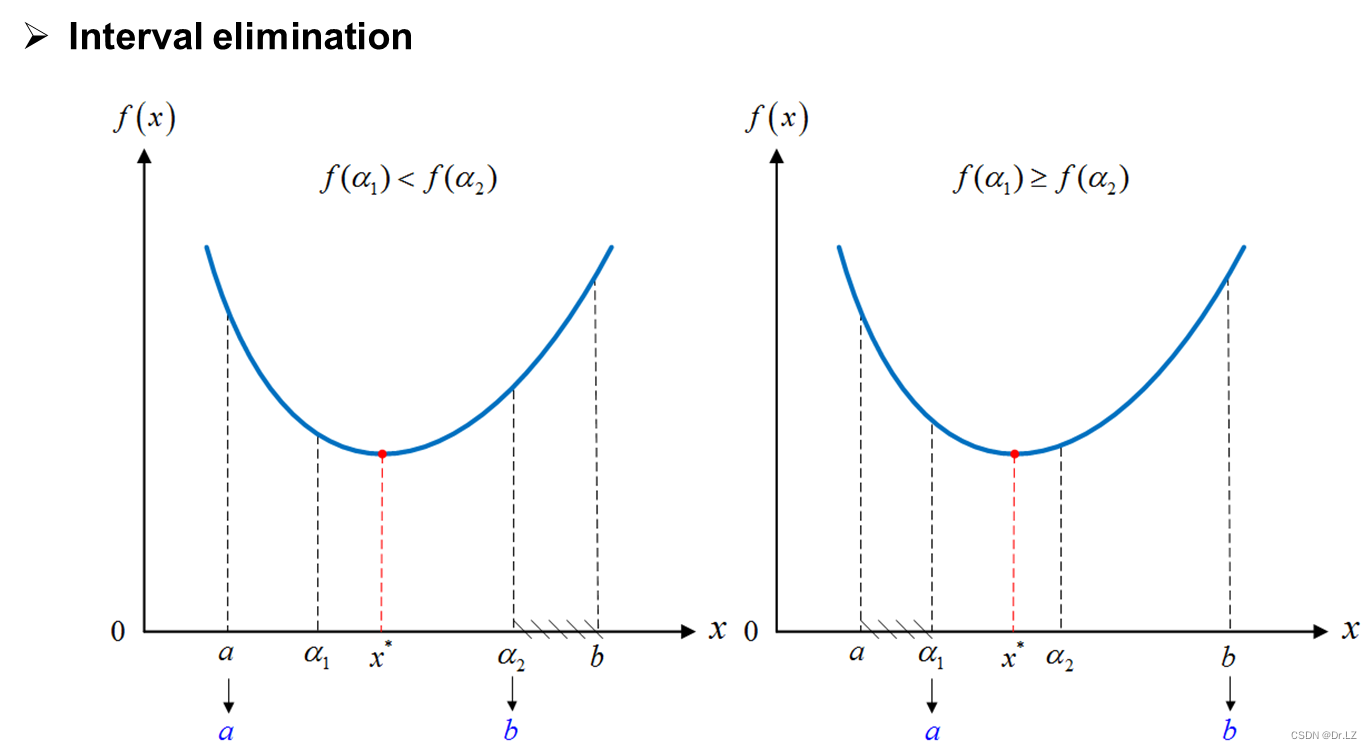

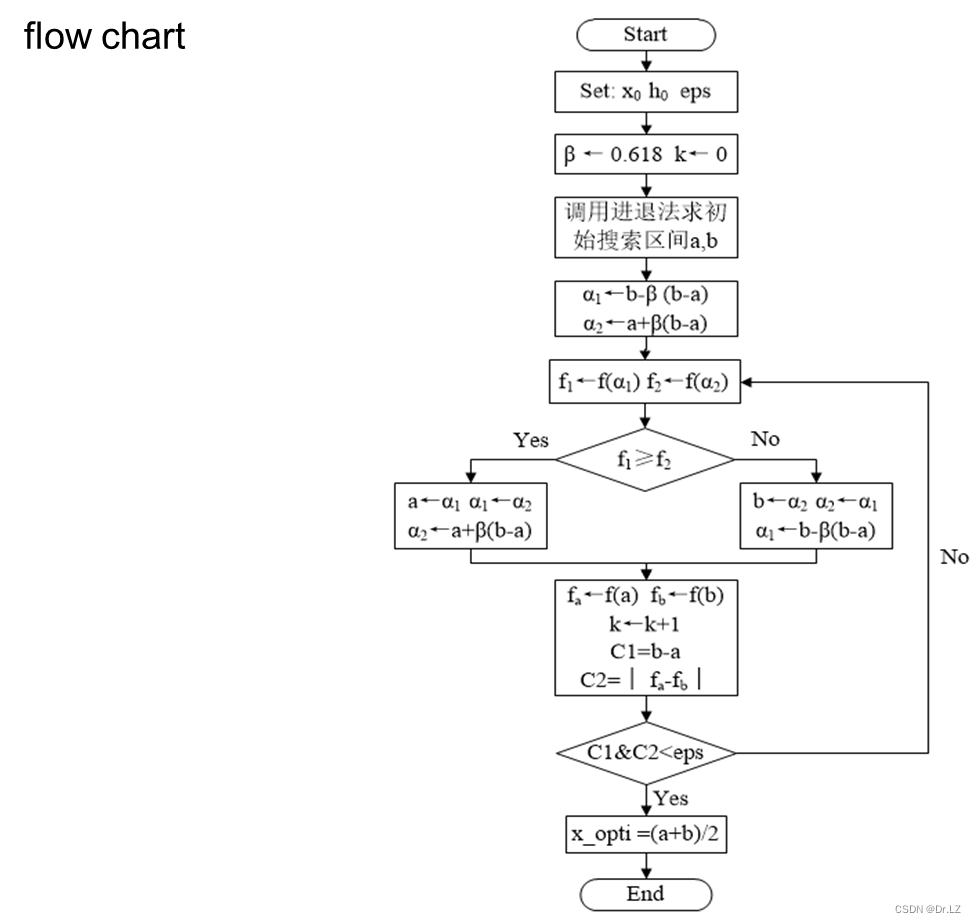
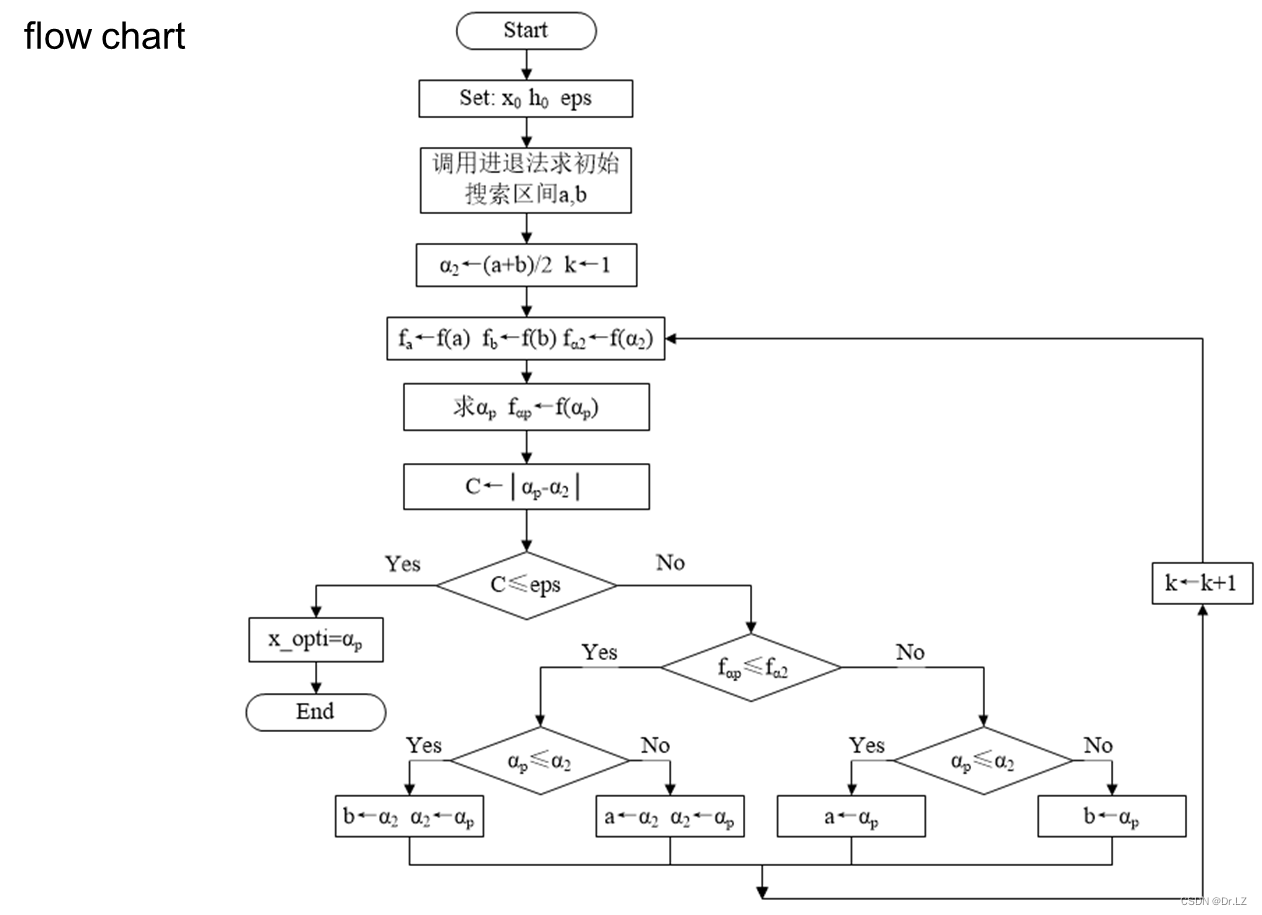
function[x_opti]=GSM(f,x0,h0,eps)
%GSM.m Golden Section Method(黄金分割法:求一维函数极小值点),调用格式[x_opti]=GSM(f,x0,h0,eps)
%x_opti:一维搜索极小值点(输出)
%f:一维目标函数(输入)
%x0:进退法初始点(输入)
%h0:进退法初始步长(输入)
%eps:收敛精度
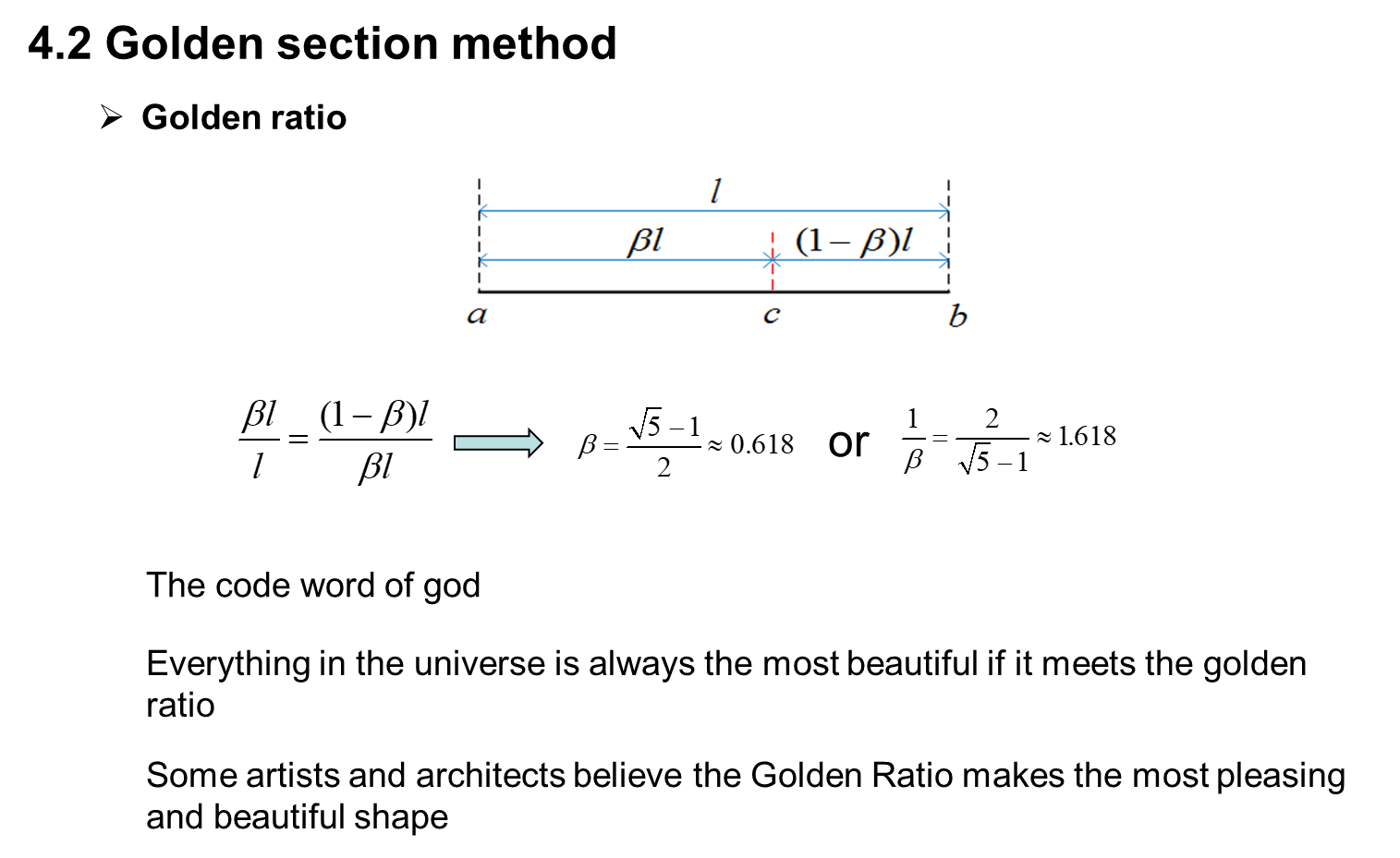
golden_ratio=(sqrt(5)-1)/2;
[a,b]=ARM(f,x0,h0);
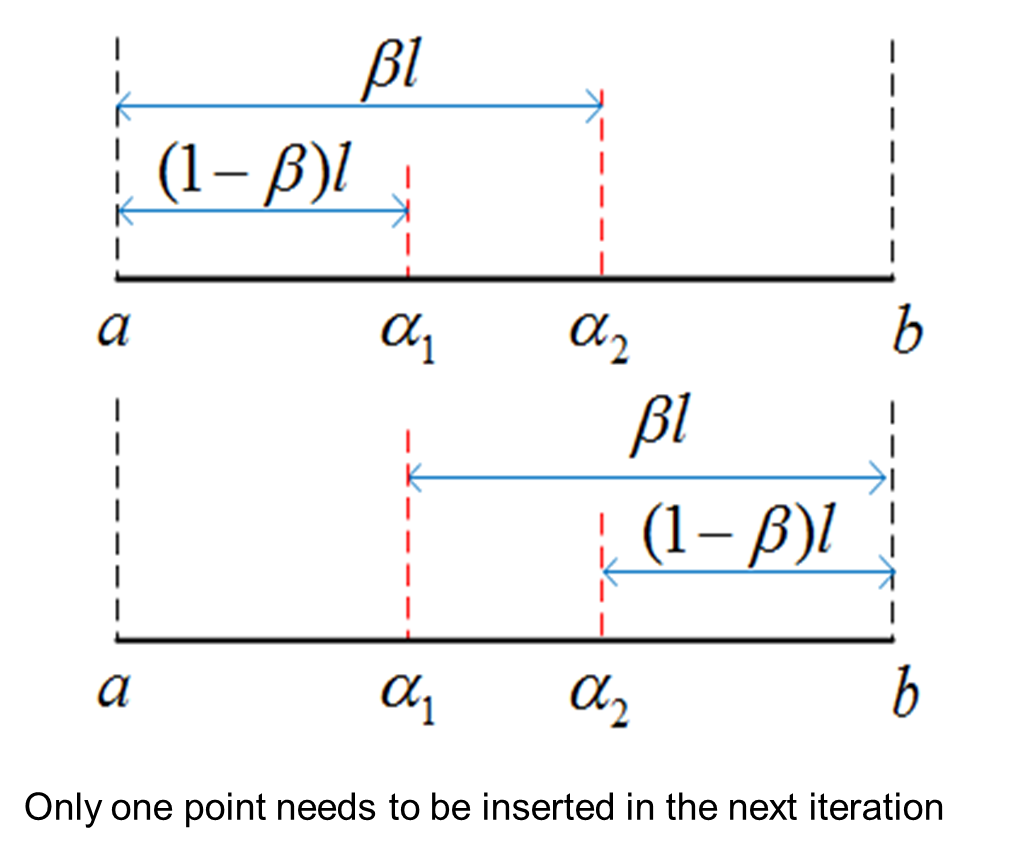
a1=b-golden_ratio*(b-a);
a2=a+golden_ratio*(b-a);
k=0;
while 1
f1=eval(subs(f,findsym(f),a1));
f2=eval(subs(f,findsym(f),a2));
if f1>=f2
a=a1;
a1=a2;
a2=a+golden_ratio*(b-a);
else
b=a2;
a2=a1;
a1=b-golden_ratio*(b-a);
end
k=k+1;
fa=eval(subs(f,findsym(f),a));
fb=eval(subs(f,findsym(f),b));
C1=b-a;
C2=abs(fa-fb);
if C1<eps&&C2<eps
break
end
end
x_opti=(a+b)/2;
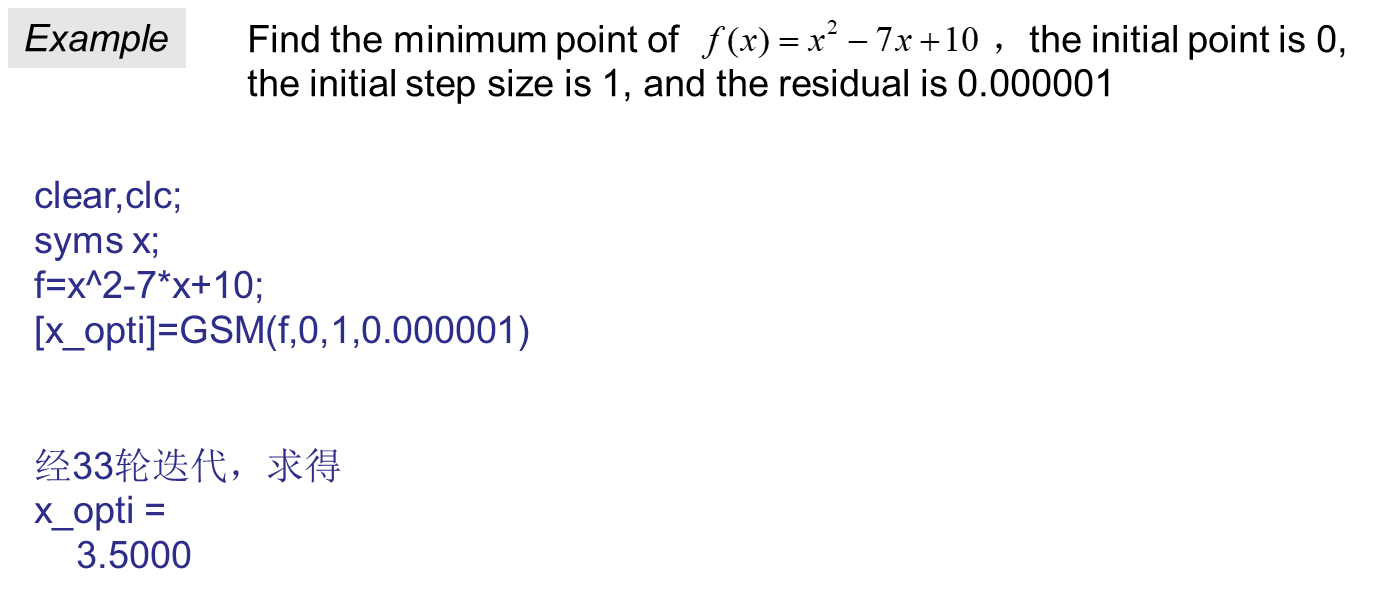
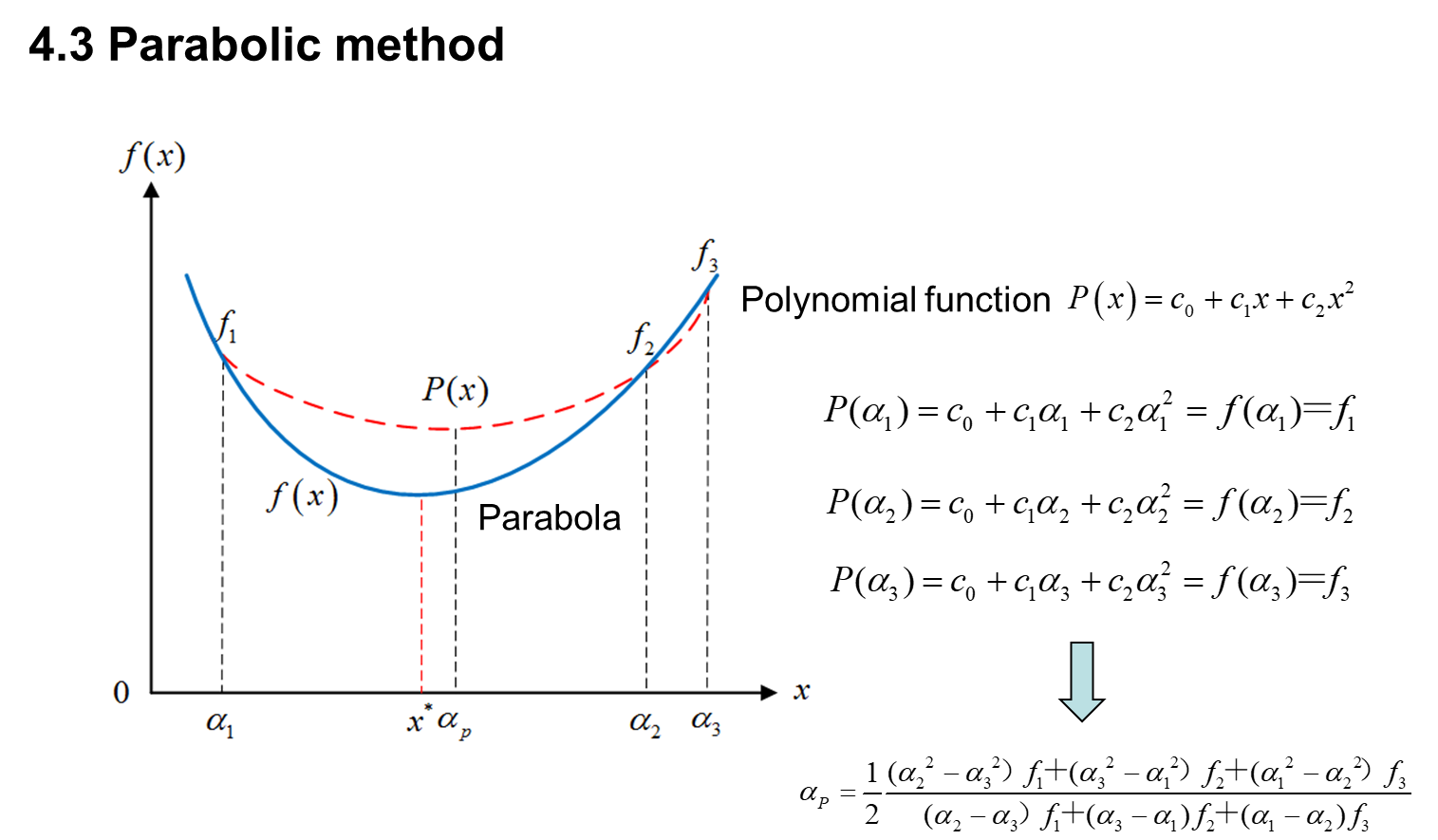
function[x_opti]=PM(f,x0,h0,eps)
%PM.m Parabolic Method(抛物线法:求一维函数极小值点),调用格式[x_opti]=PM(f,x0,h0,eps)
%x_opti:一维搜索极小值点(输出)
%f:一维目标函数(输入)
%x0:进退法初始点(输入)
%h0:进退法初始步长(输入)
%eps:收敛精度(输入)
[a,b]=ARM(f,x0,h0);
a2=(a+b)/2;
k=1;
while 1
fa=eval(subs(f,findsym(f),a));
fb=eval(subs(f,findsym(f),b));
fa2=eval(subs(f,findsym(f),a2));
c1=fa*(a2^2-b^2)+fa2*(b^2-a^2)+fb*(a^2-a2^2);
c2=fa*(a2-b)+fa2*(b-a)+fb*(a-a2);
ap=c1/2/c2;
fap=eval(subs(f,findsym(f),ap));
C=abs(ap-a2);
if C<eps
break
end
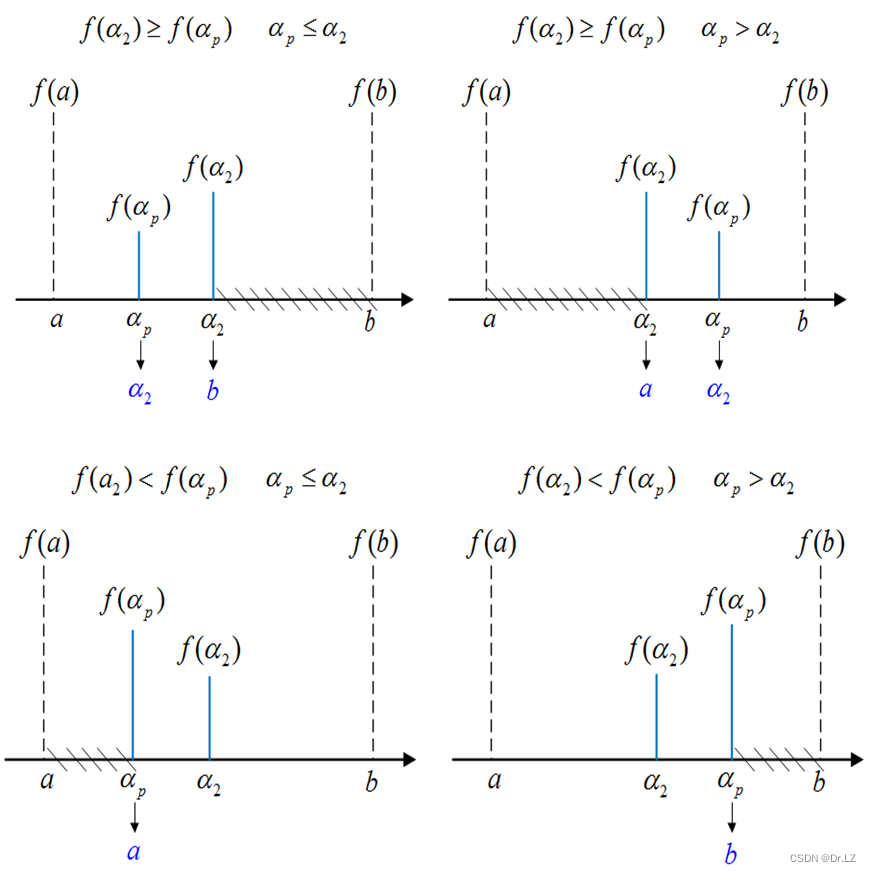
if fap<=fa2
if ap<=a2
b=a2;
a2=ap;
else
a=a2;
a2=ap;
end
else
if ap<=a2
a=ap;
else
b=ap;
end
end
k=k+1;
end
x_opti=ap;
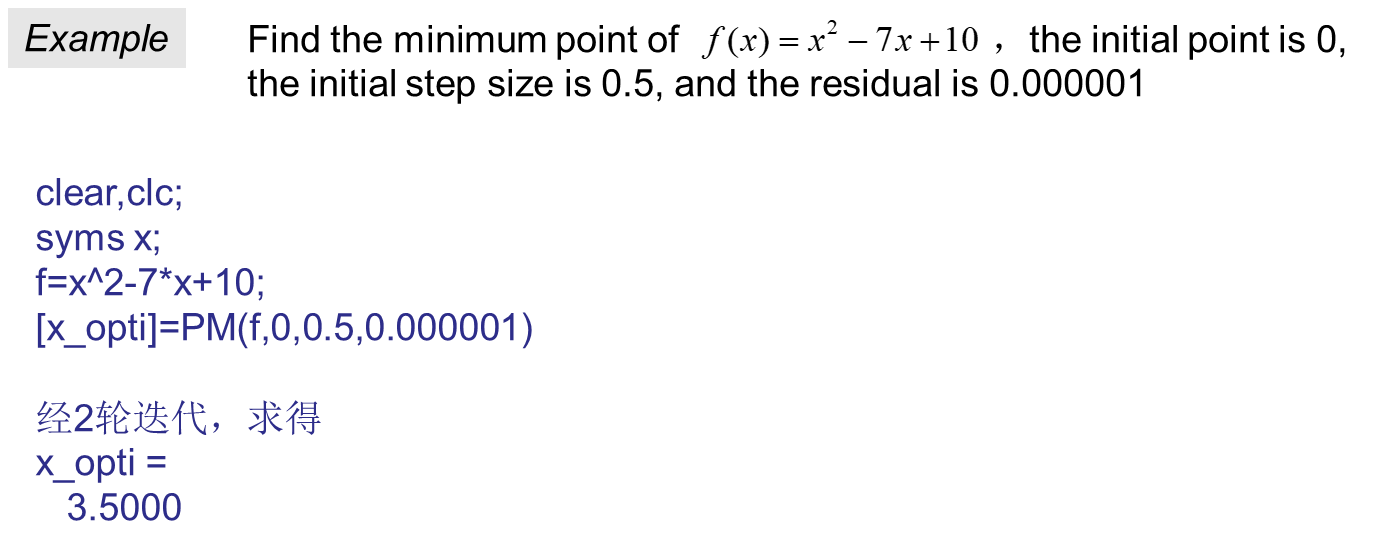
function[x_opti]=NM(f,x0,eps)
%NM.m Newton Method(牛顿法:求一维函数极小值点),调用格式[x_opti]=NM(f,x0,eps)
%x_opti:一维搜索极小值点(输出)
%f:一维目标函数(输入)
%x0:初始点(输入)
%eps:收敛精度(输入)
df_exp=diff(f);
ddf_exp=diff(df_exp);
k=0;
while 1
df_val=eval(subs(df_exp,findsym(df_exp),x0));
C=abs(df_val);
if C<eps
break
end
ddf_val=eval(subs(ddf_exp,findsym(ddf_exp),x0));
x1=x0-df_val/ddf_val; %求迭代点x1
k=k+1;
x0=x1;
end
x_opti=x0;
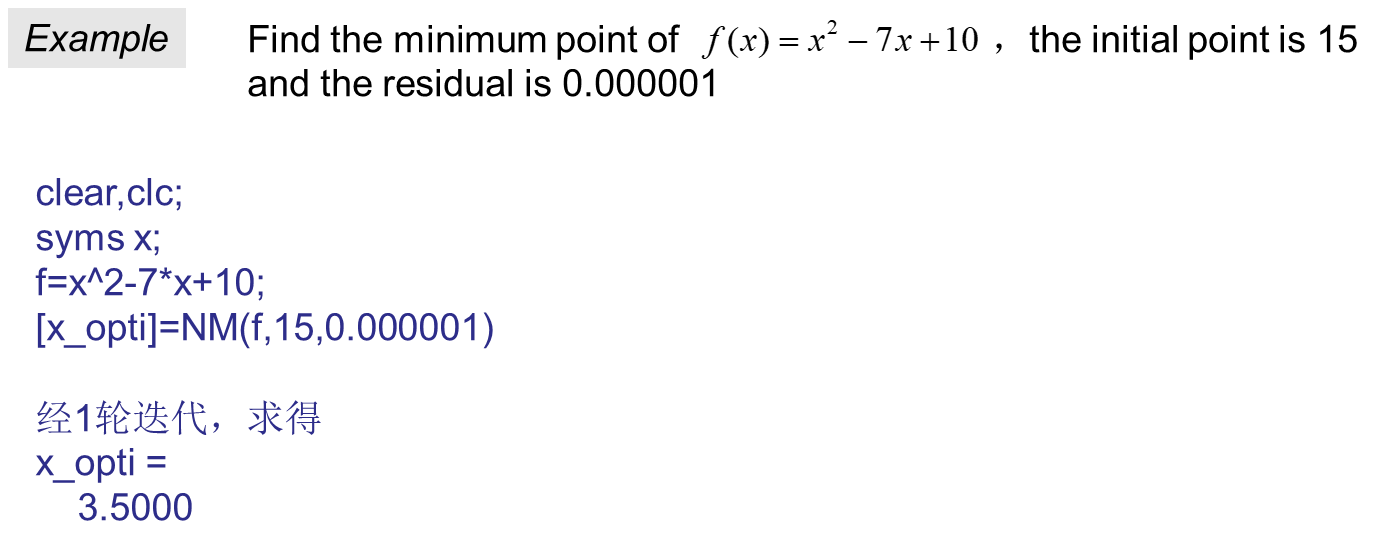
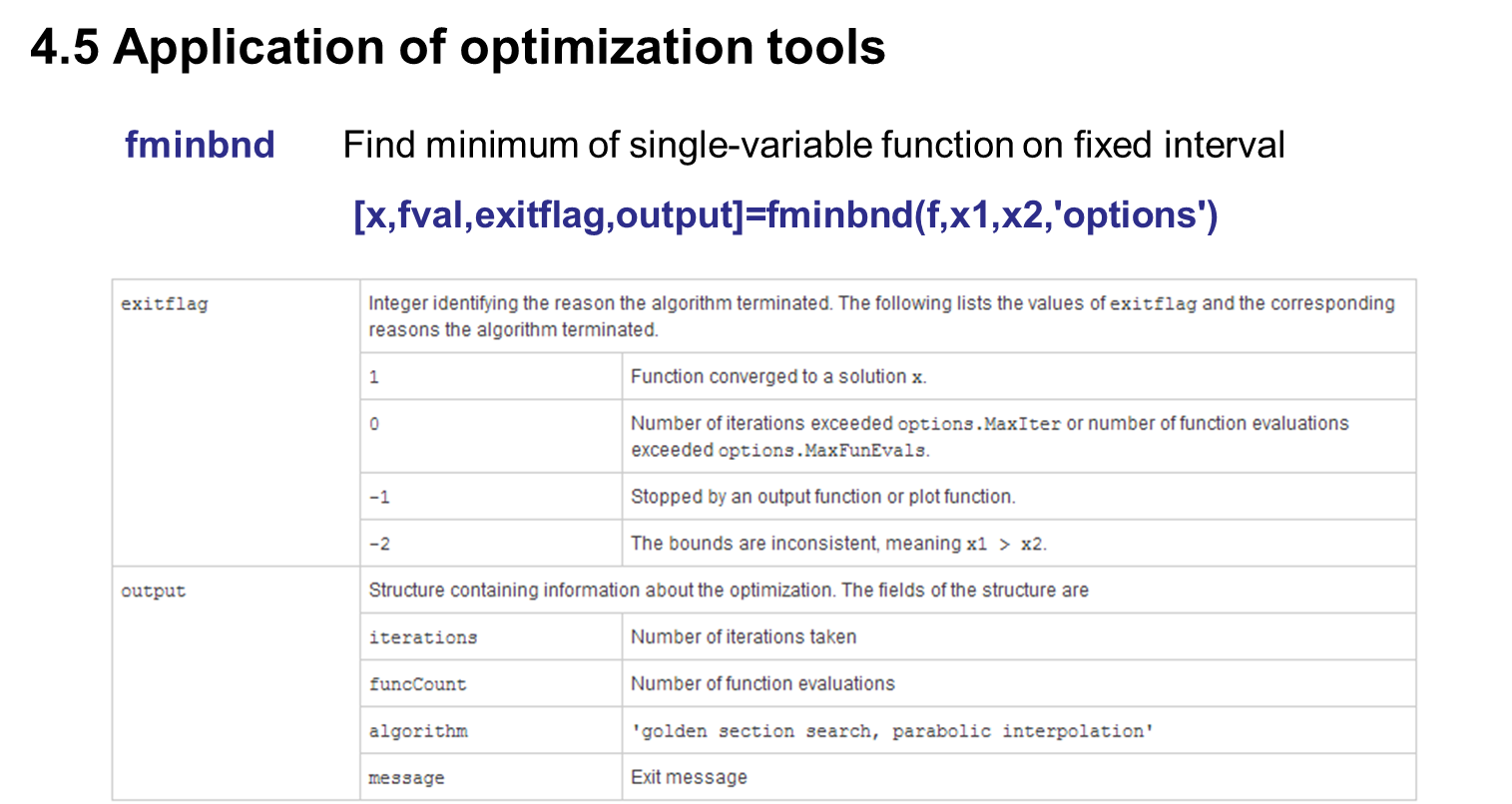
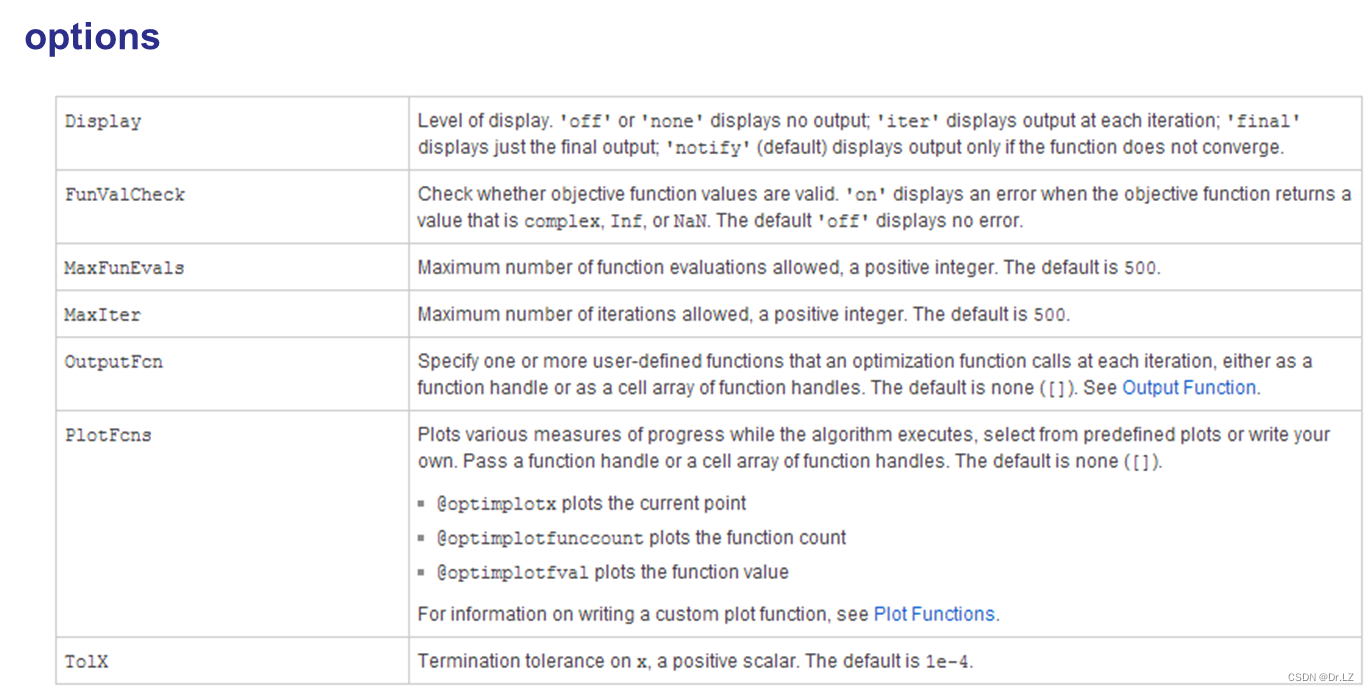

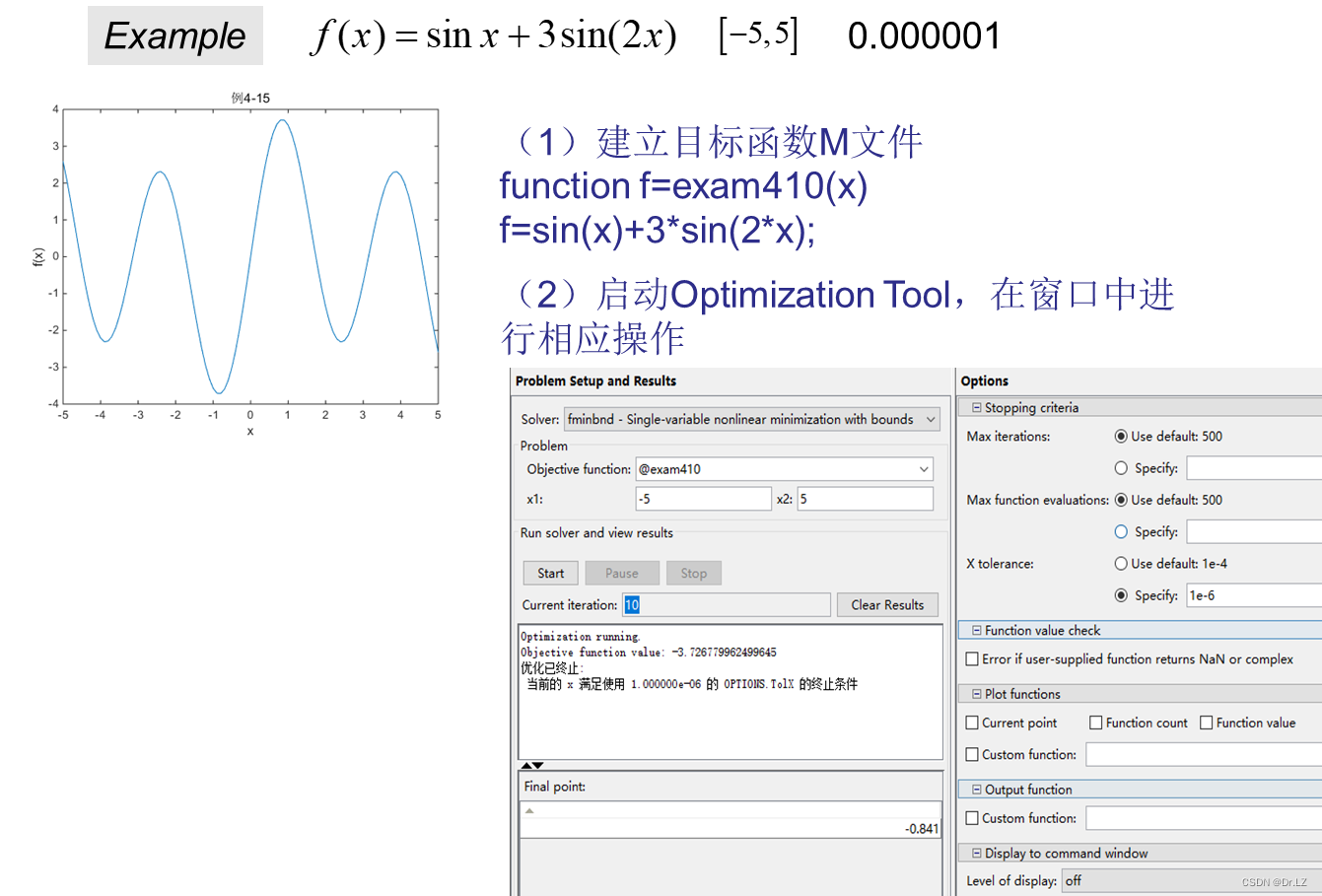

五、 Unconstrained optimization

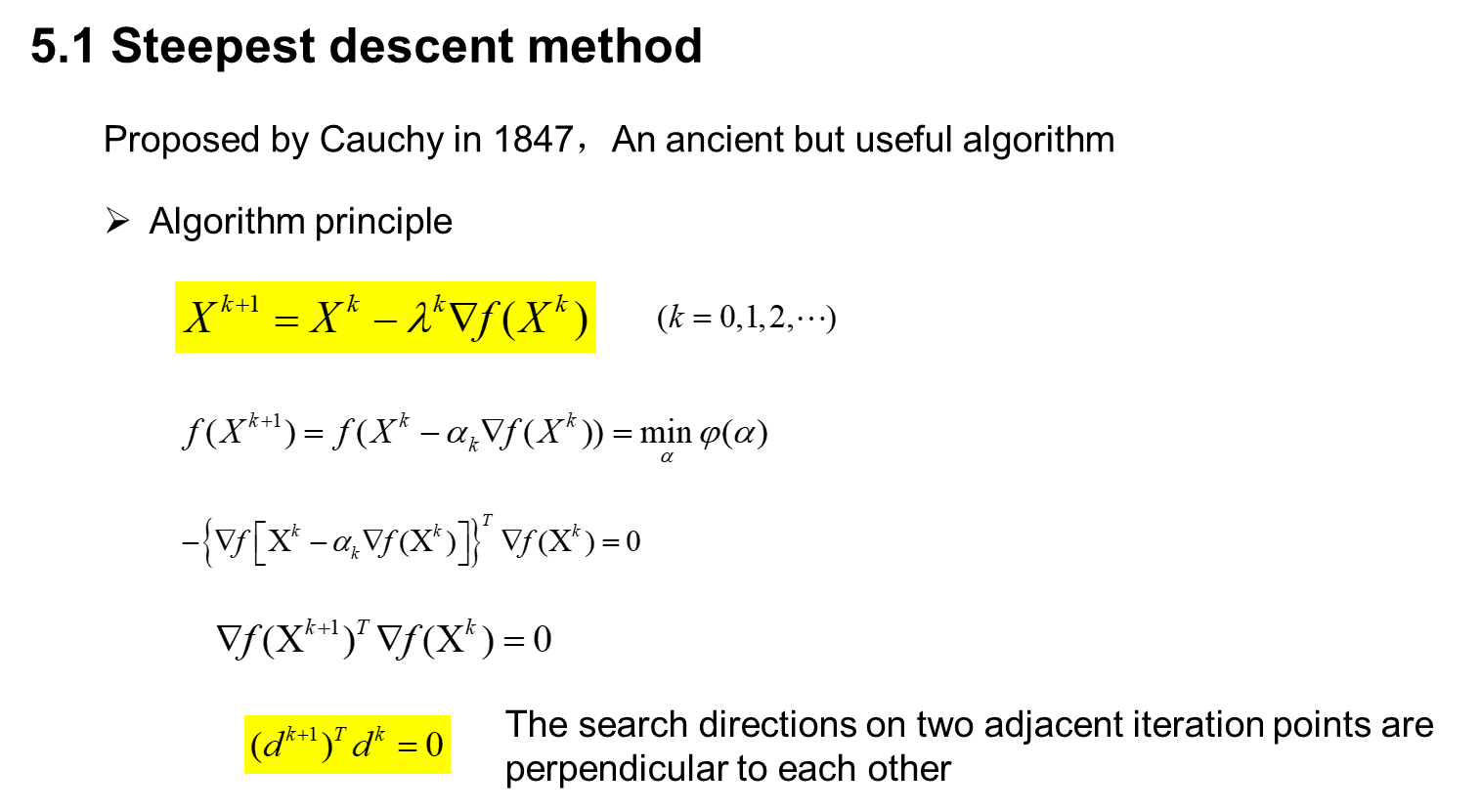




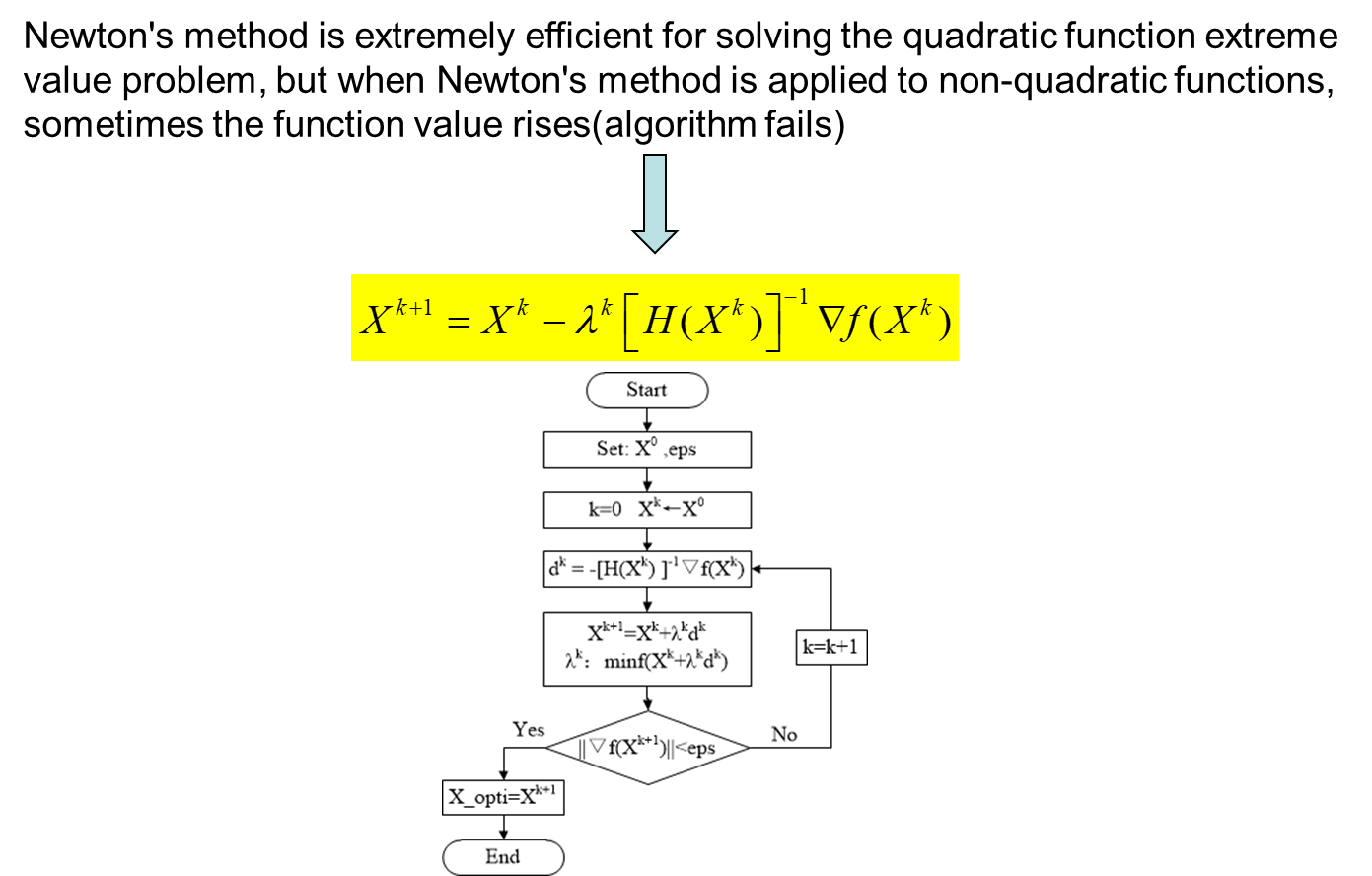



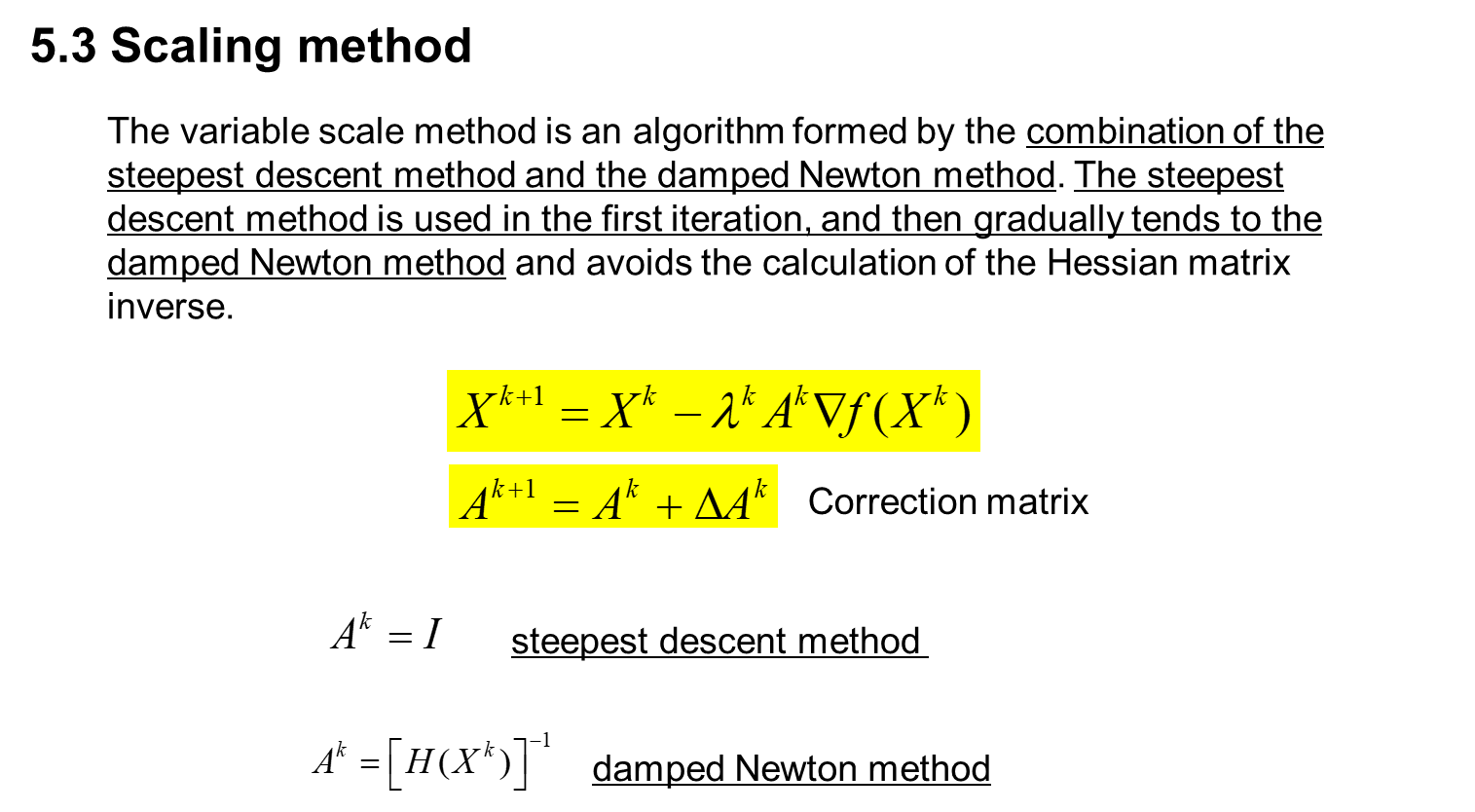

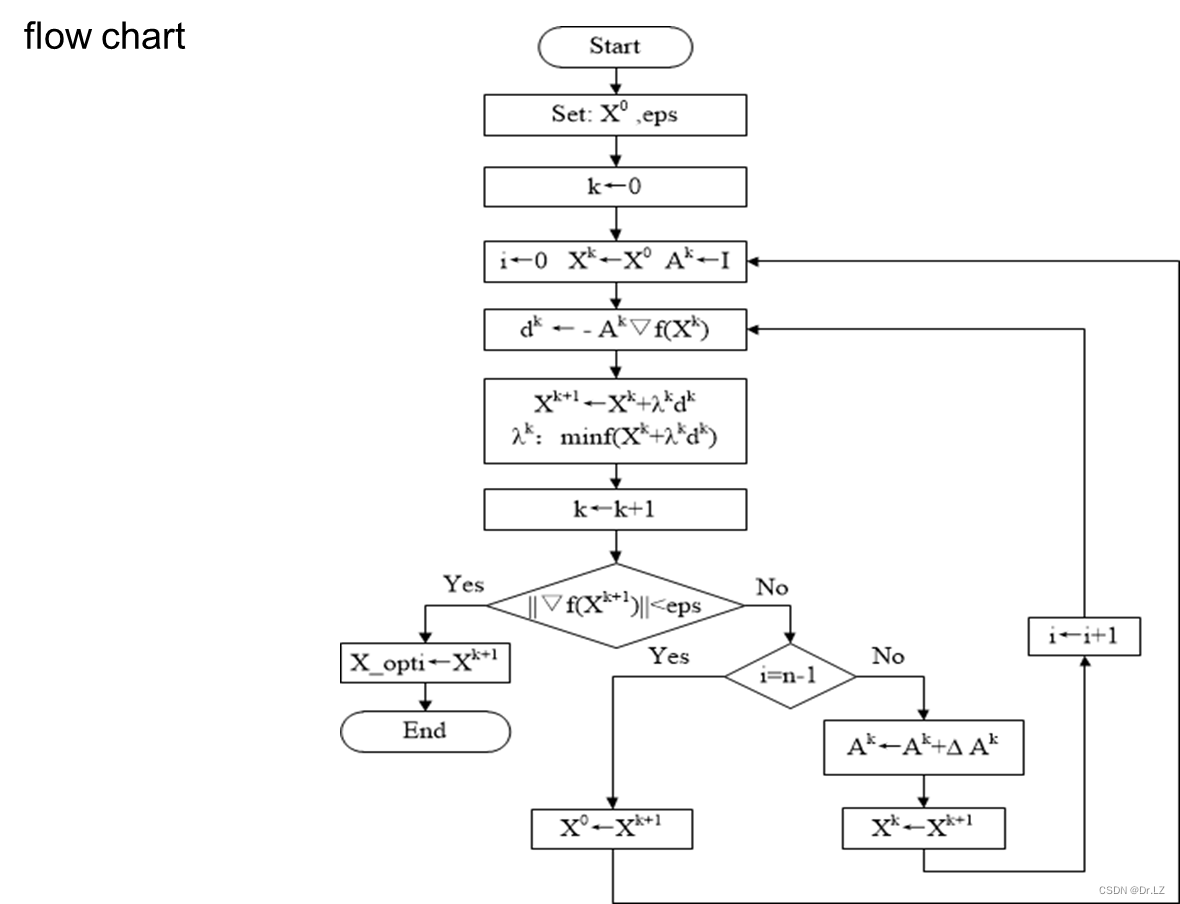


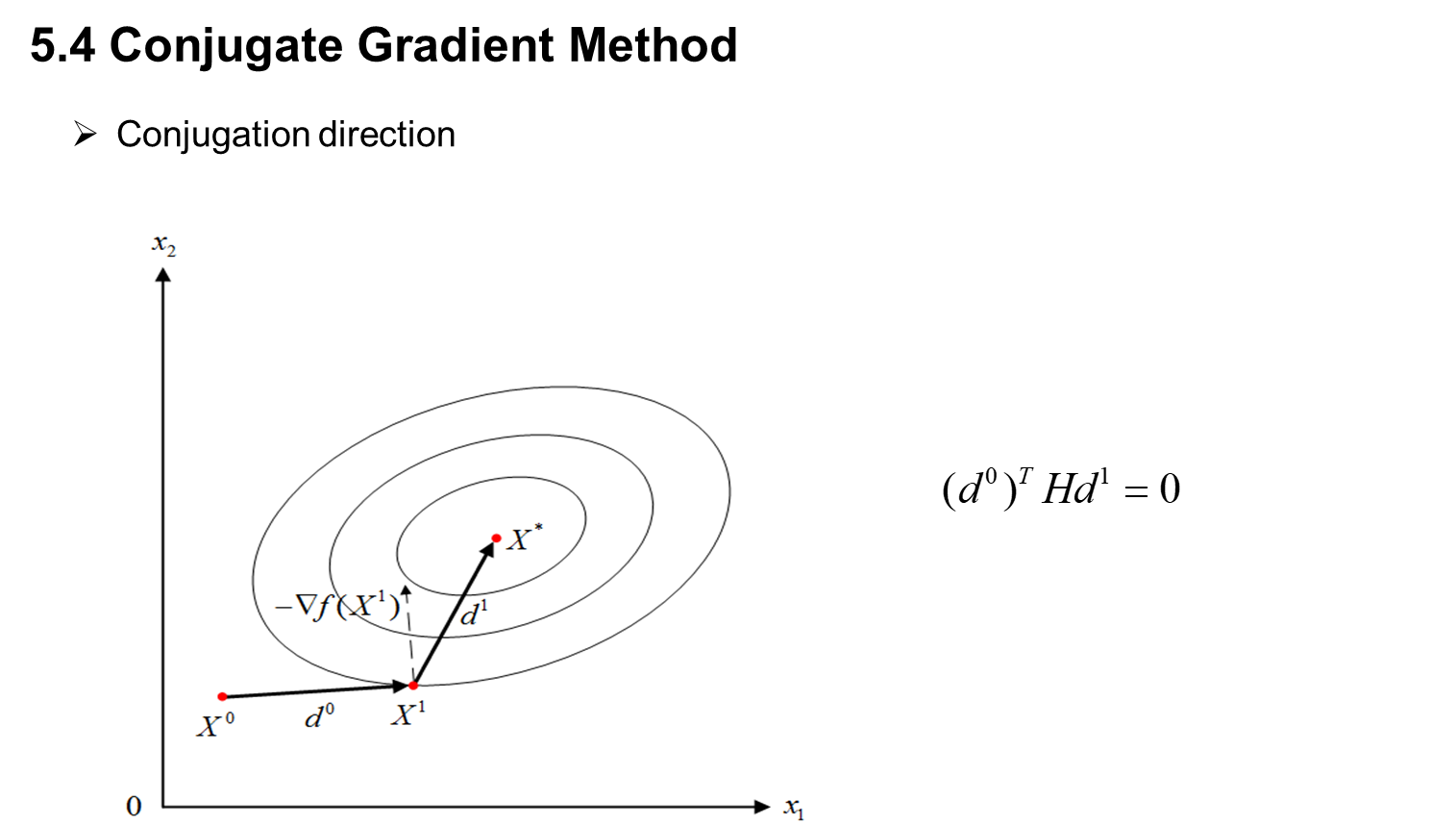
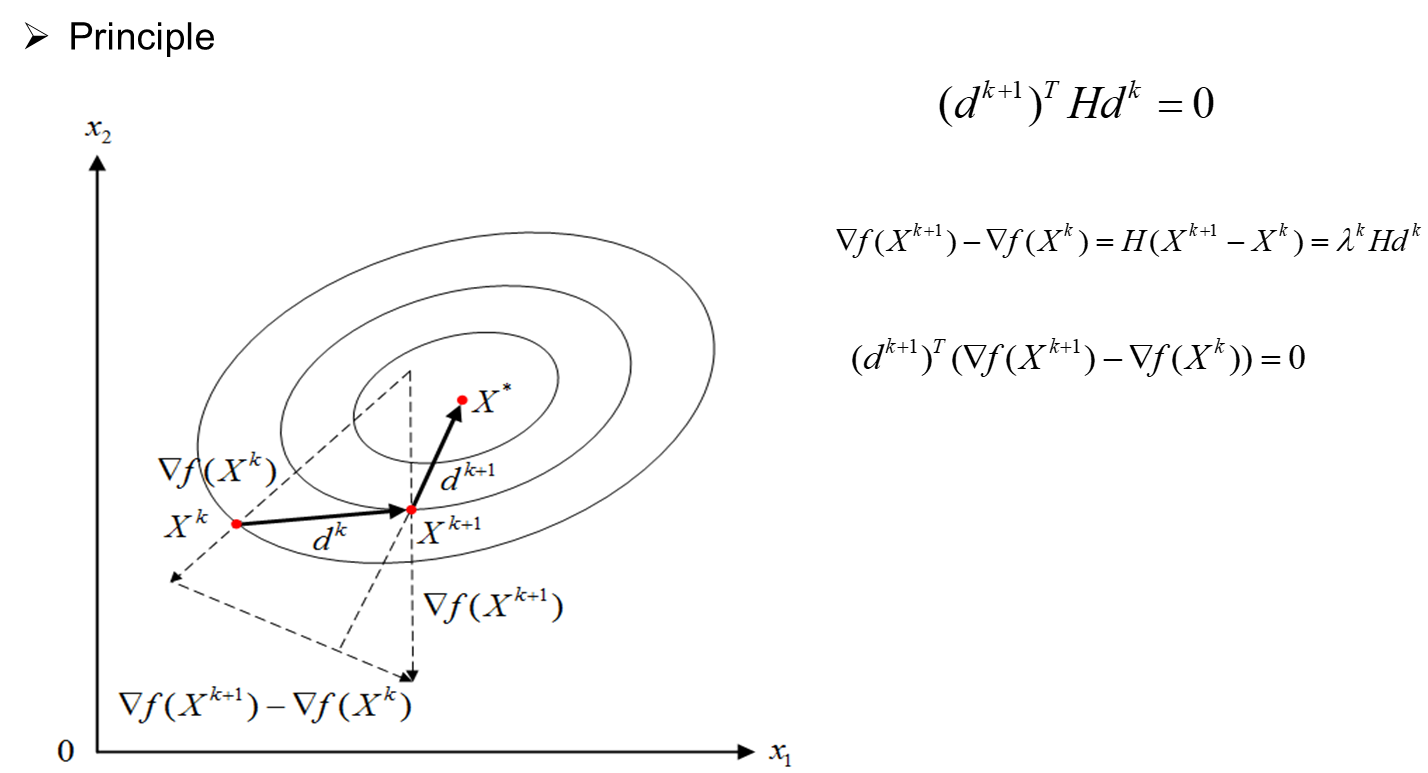
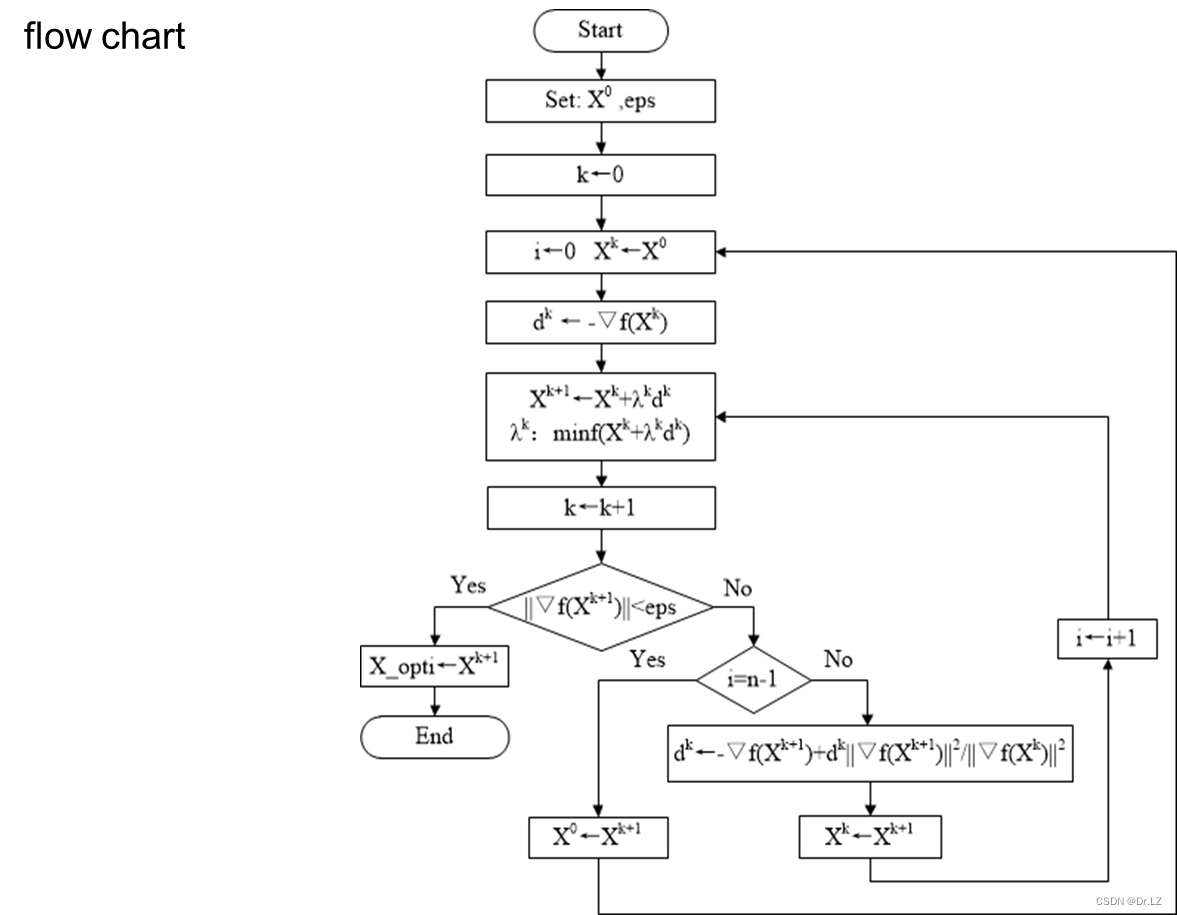



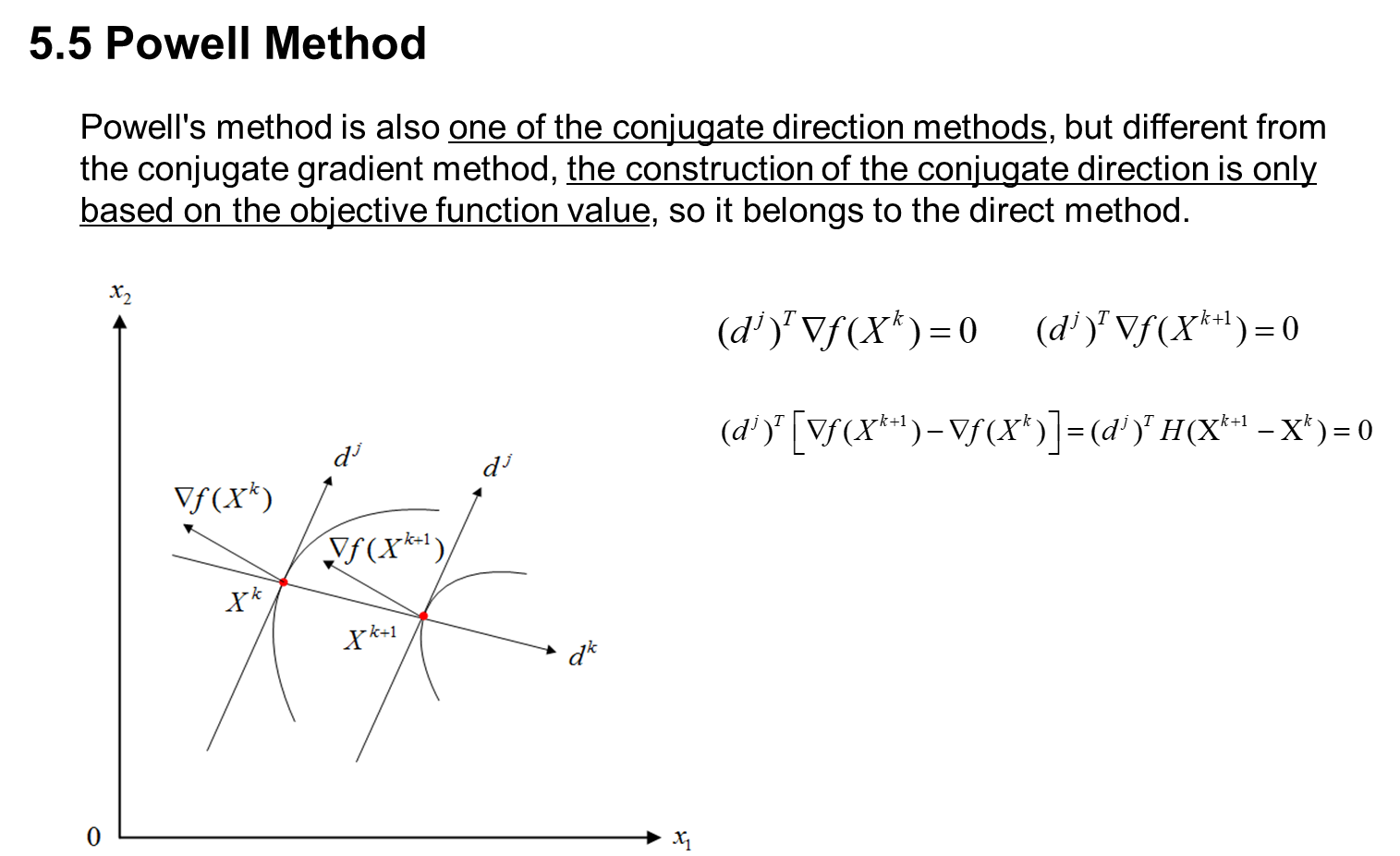
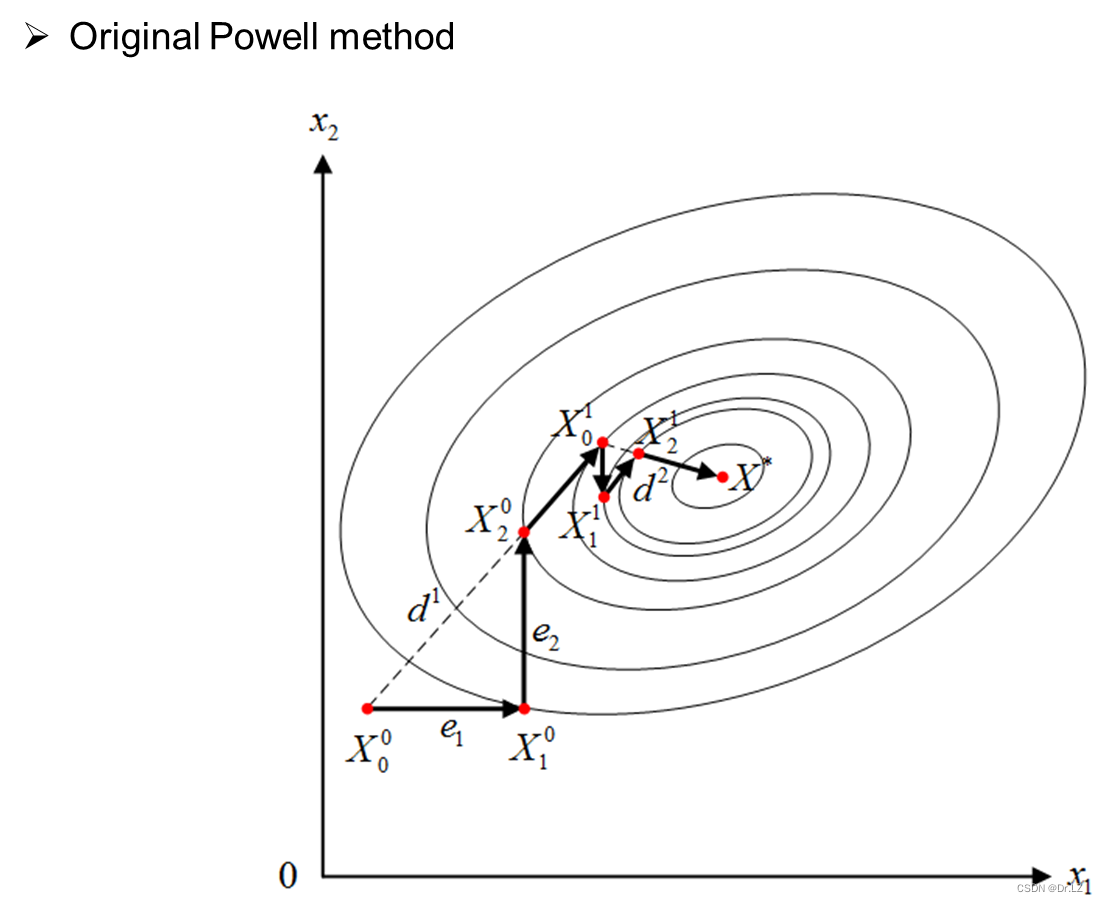
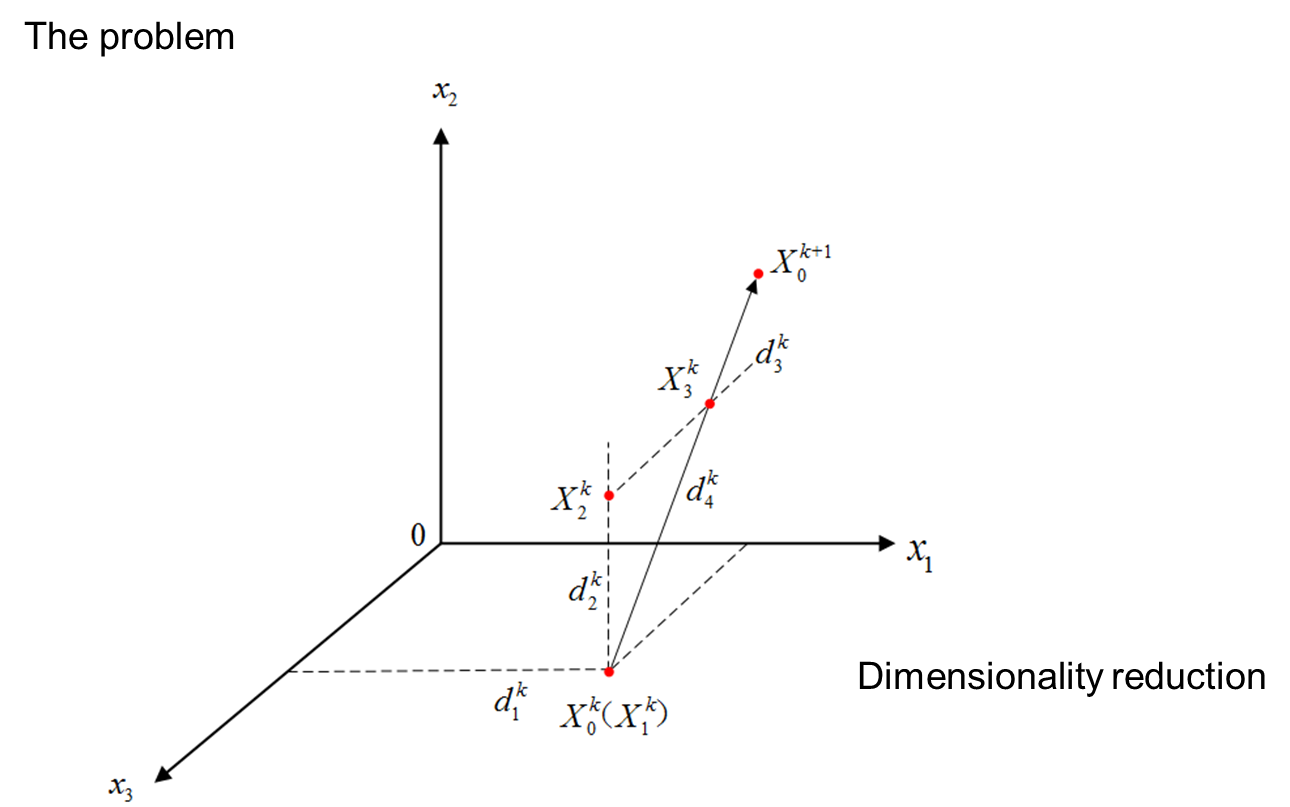
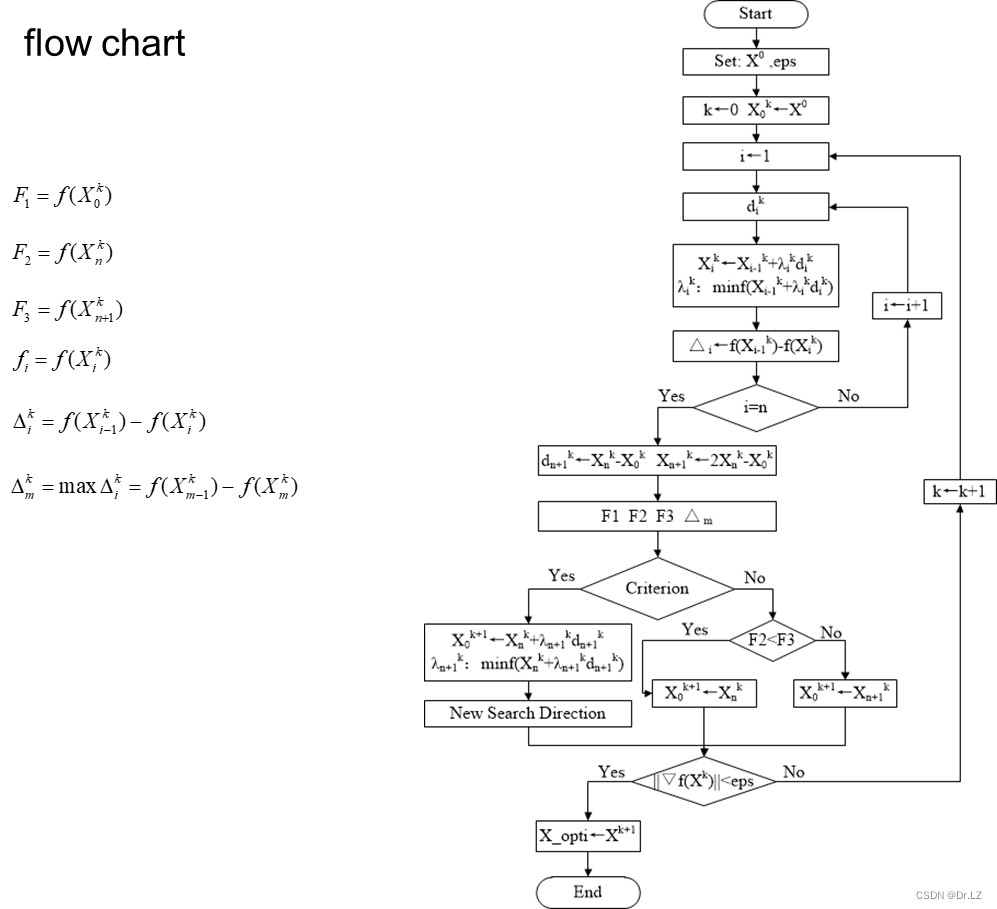


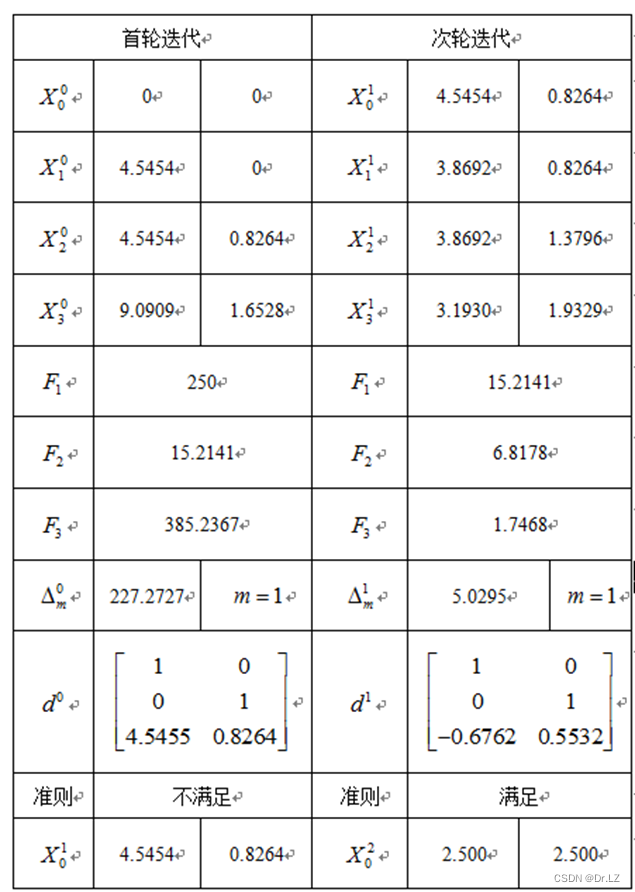


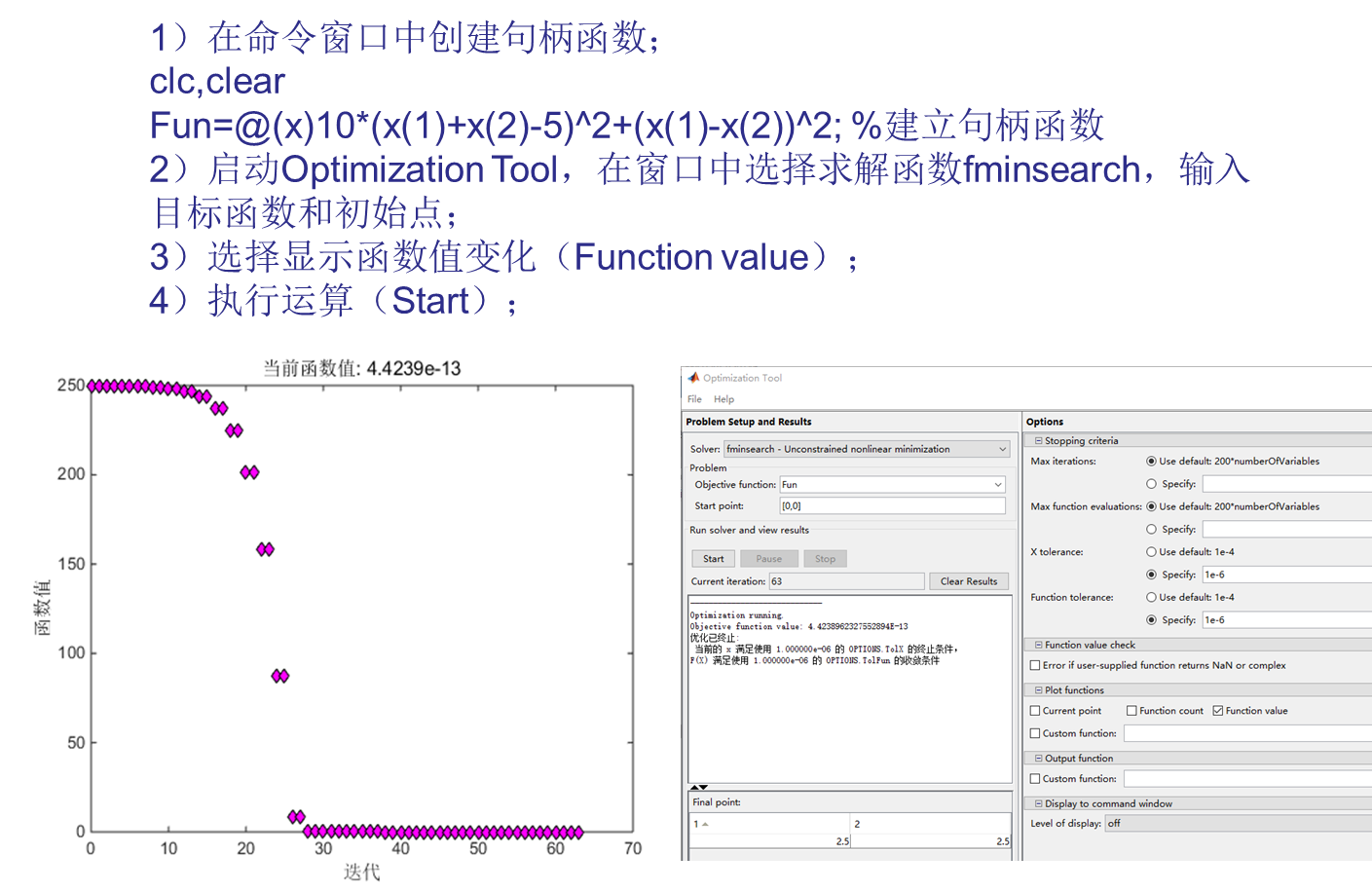

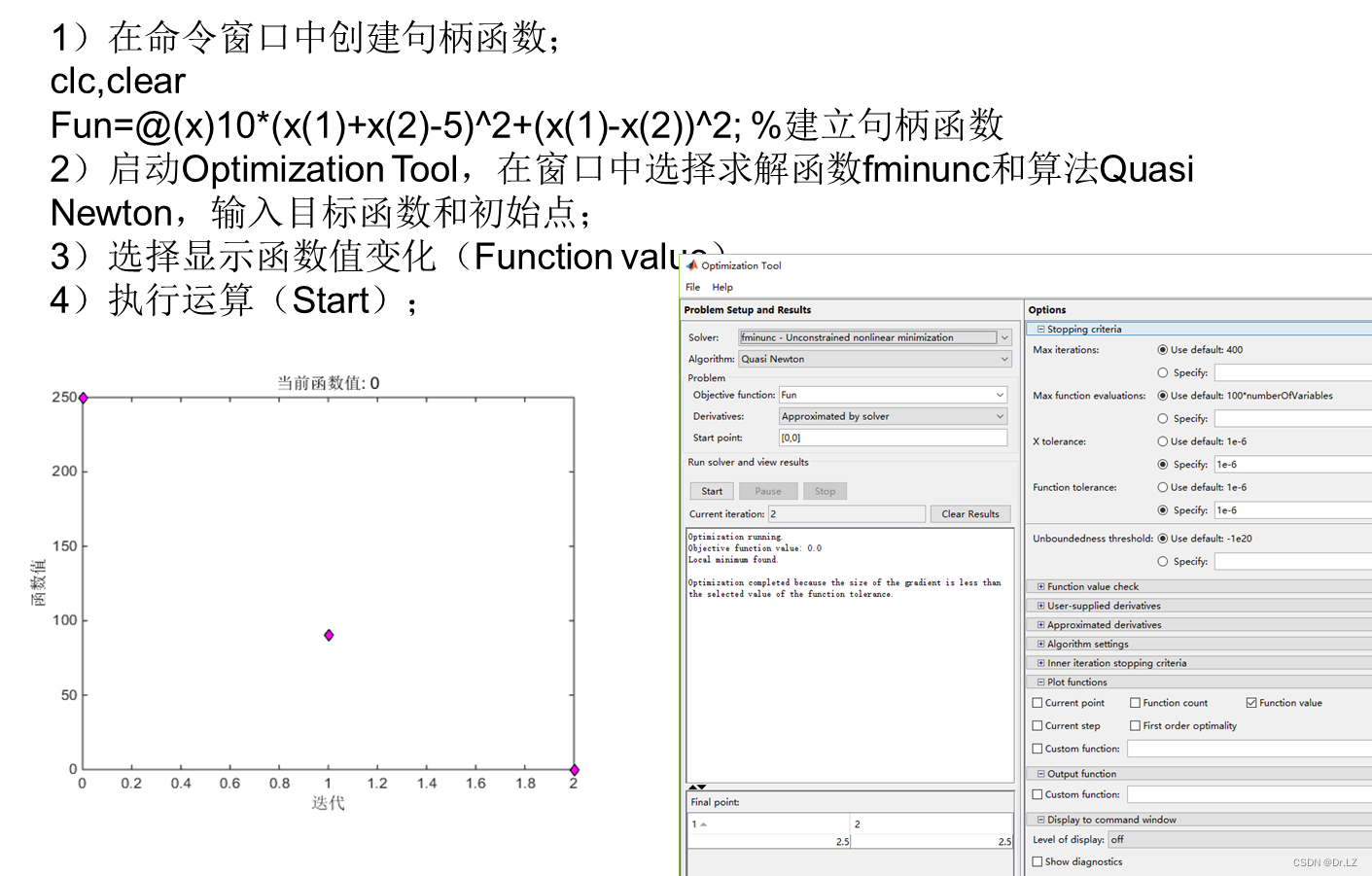

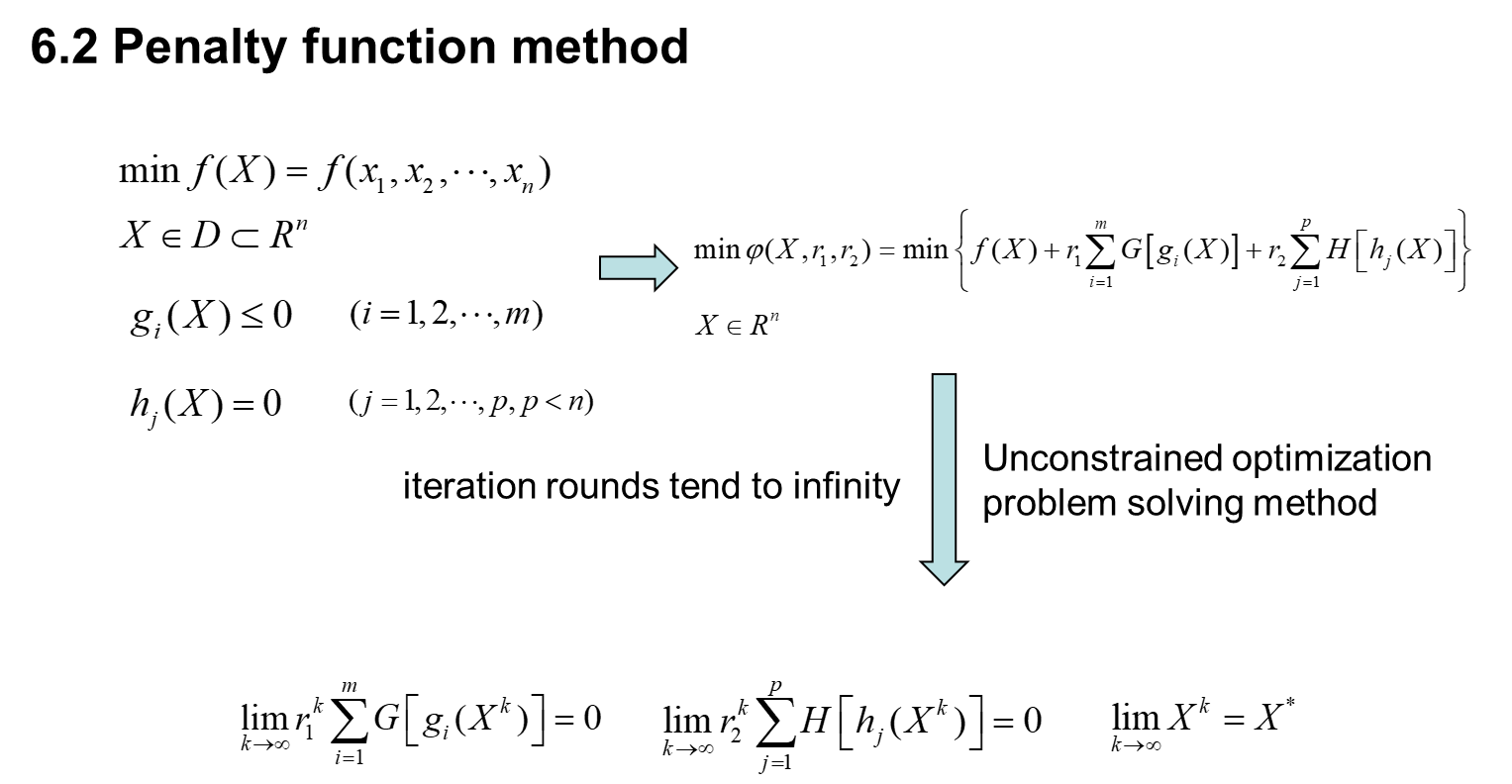
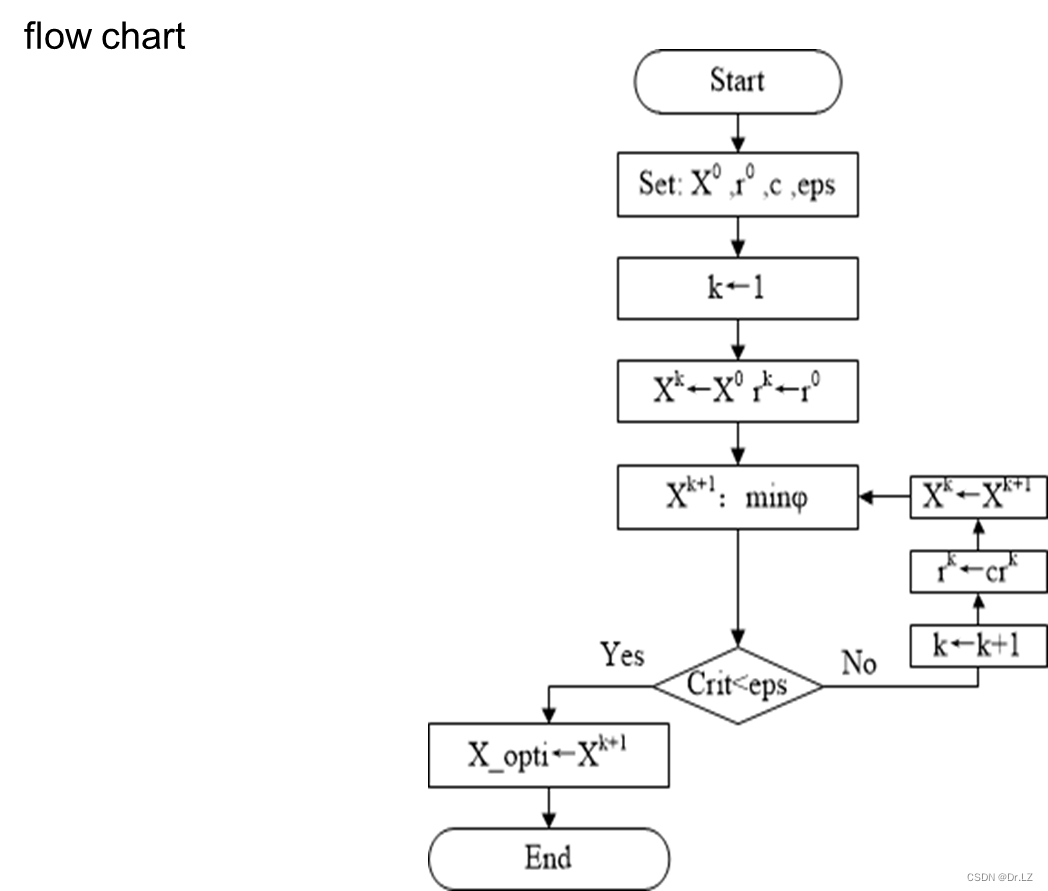
六、 Constrained optimization

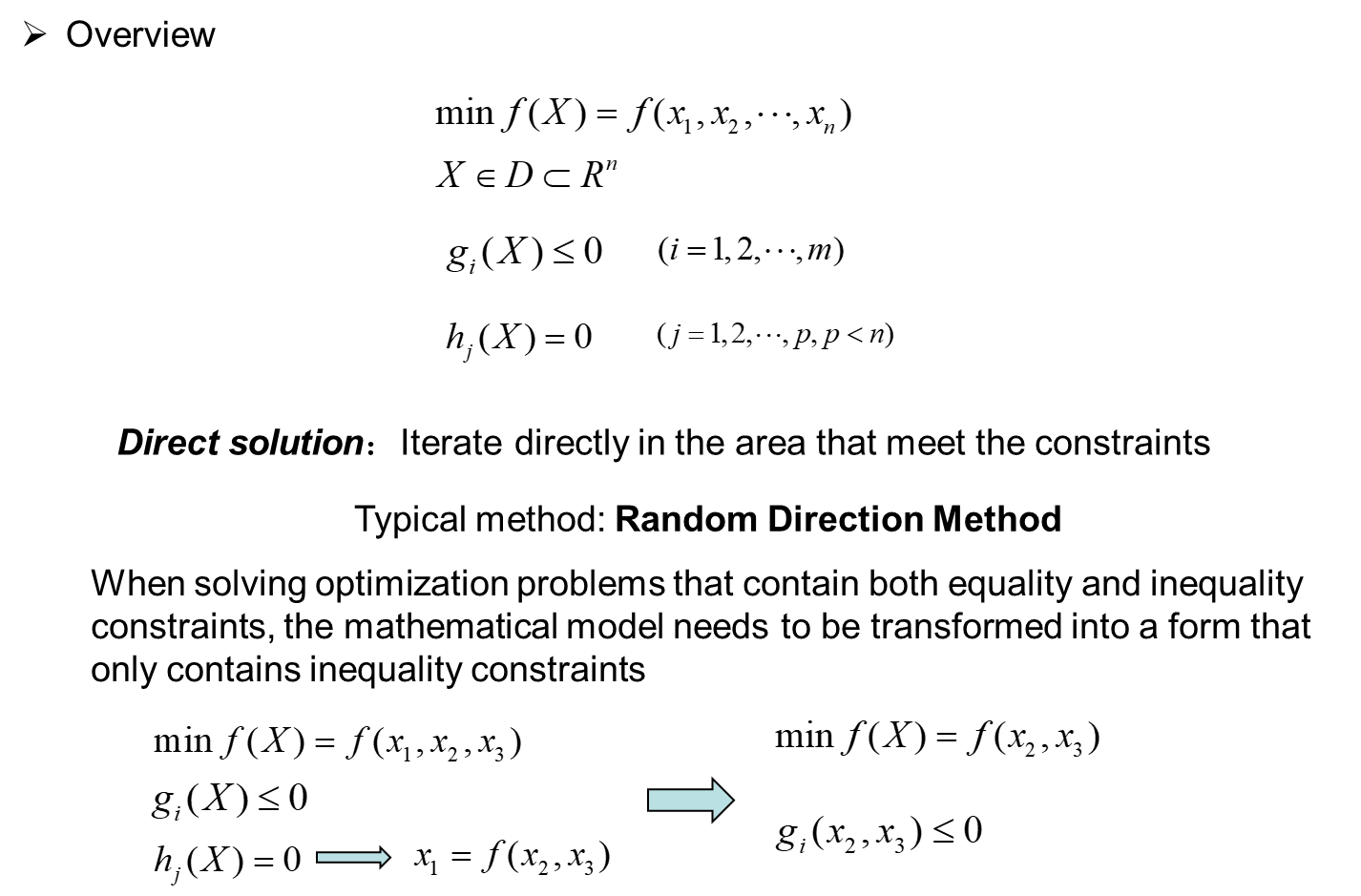
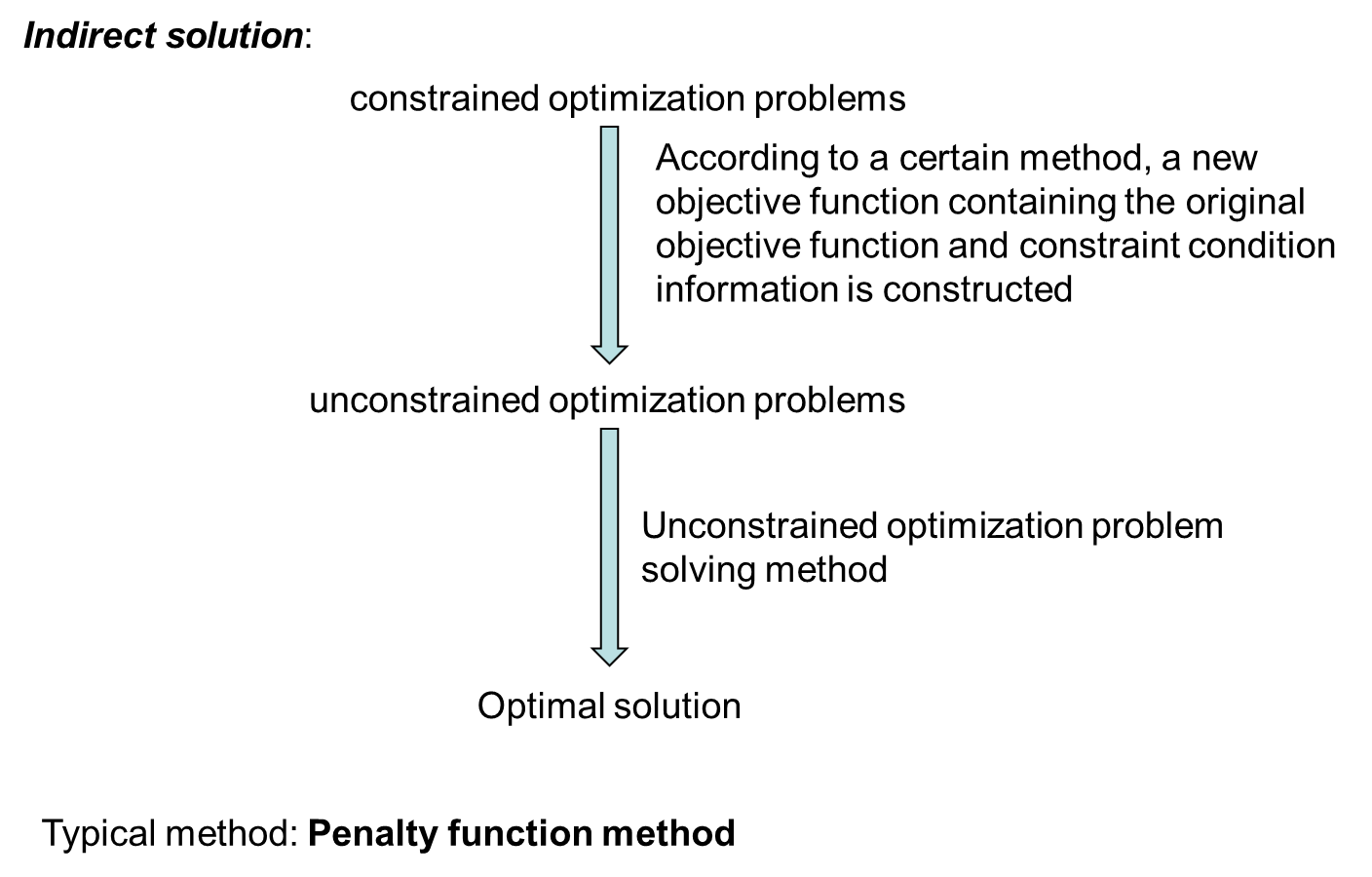


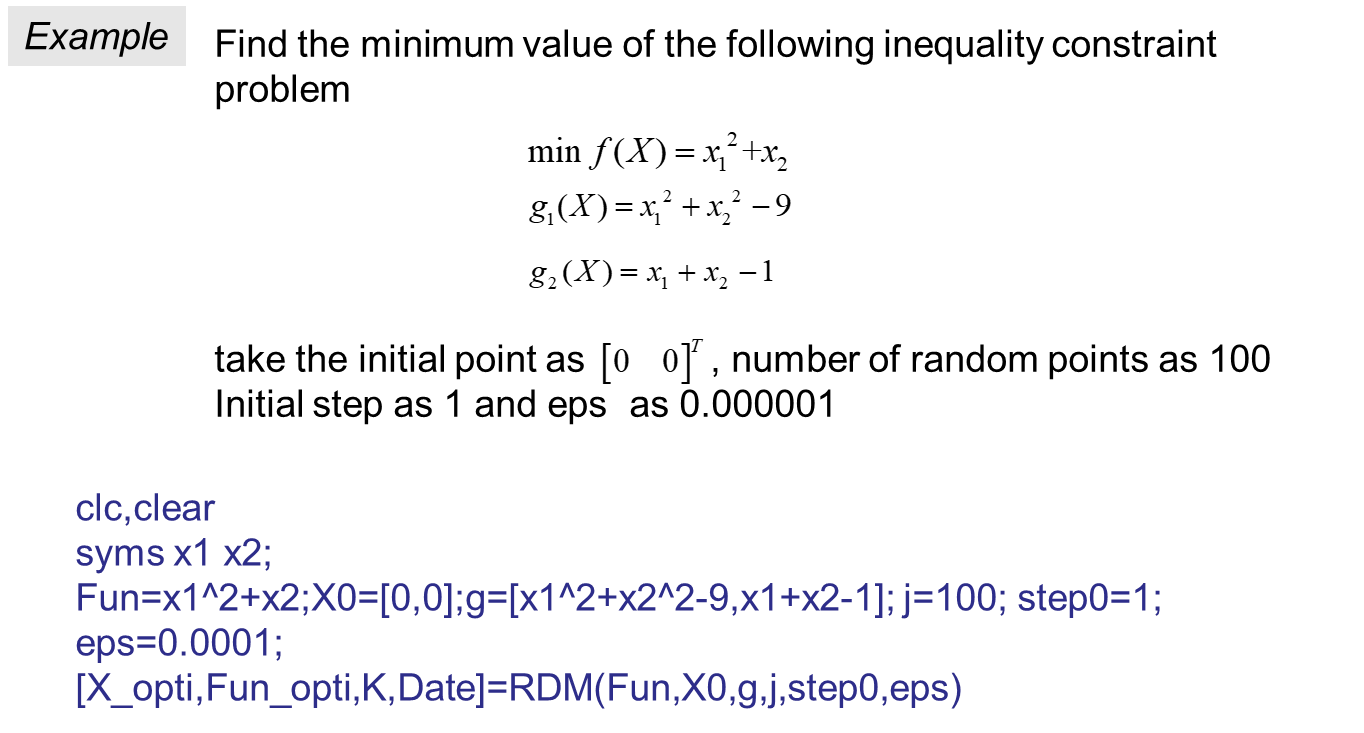
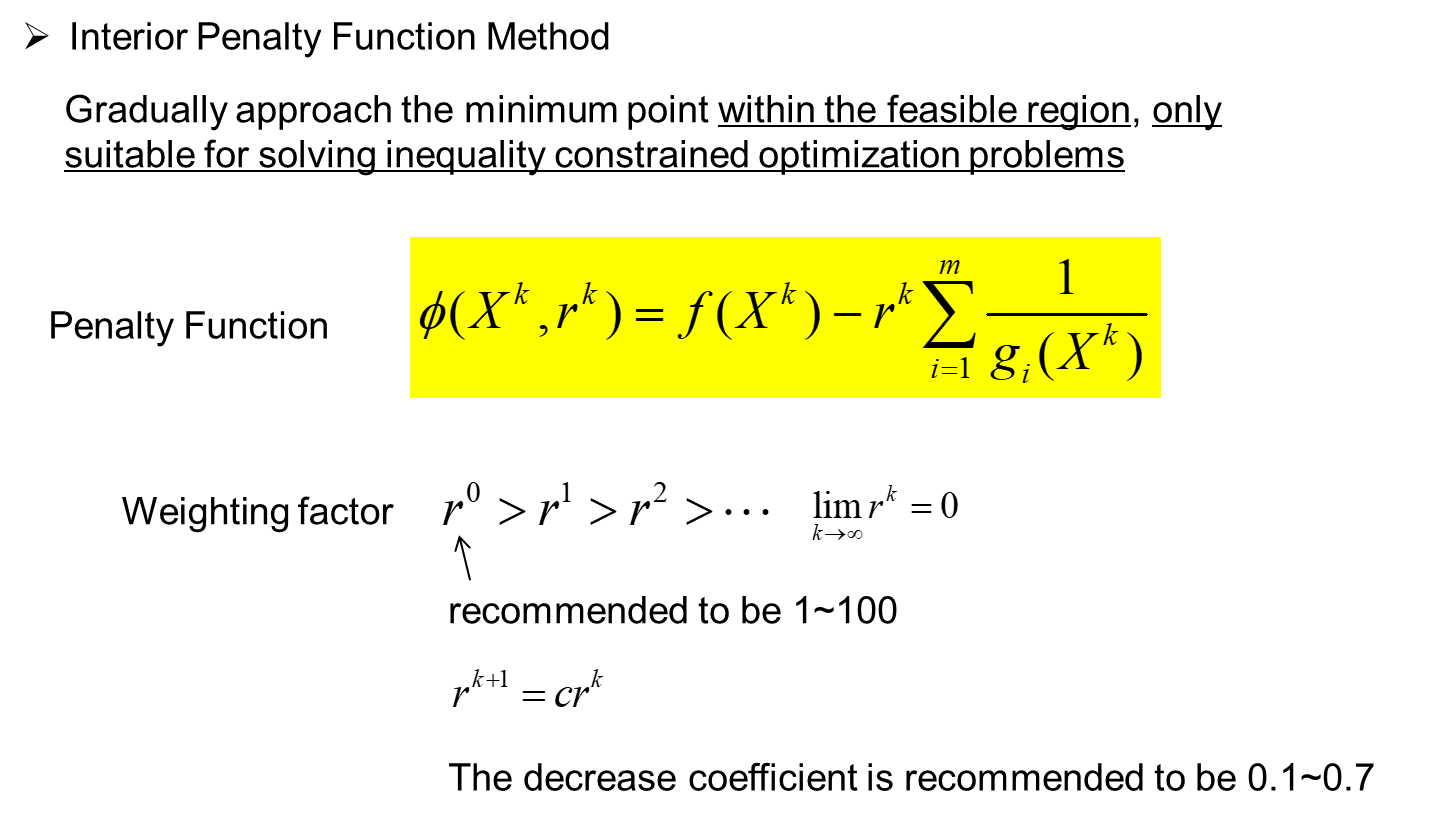


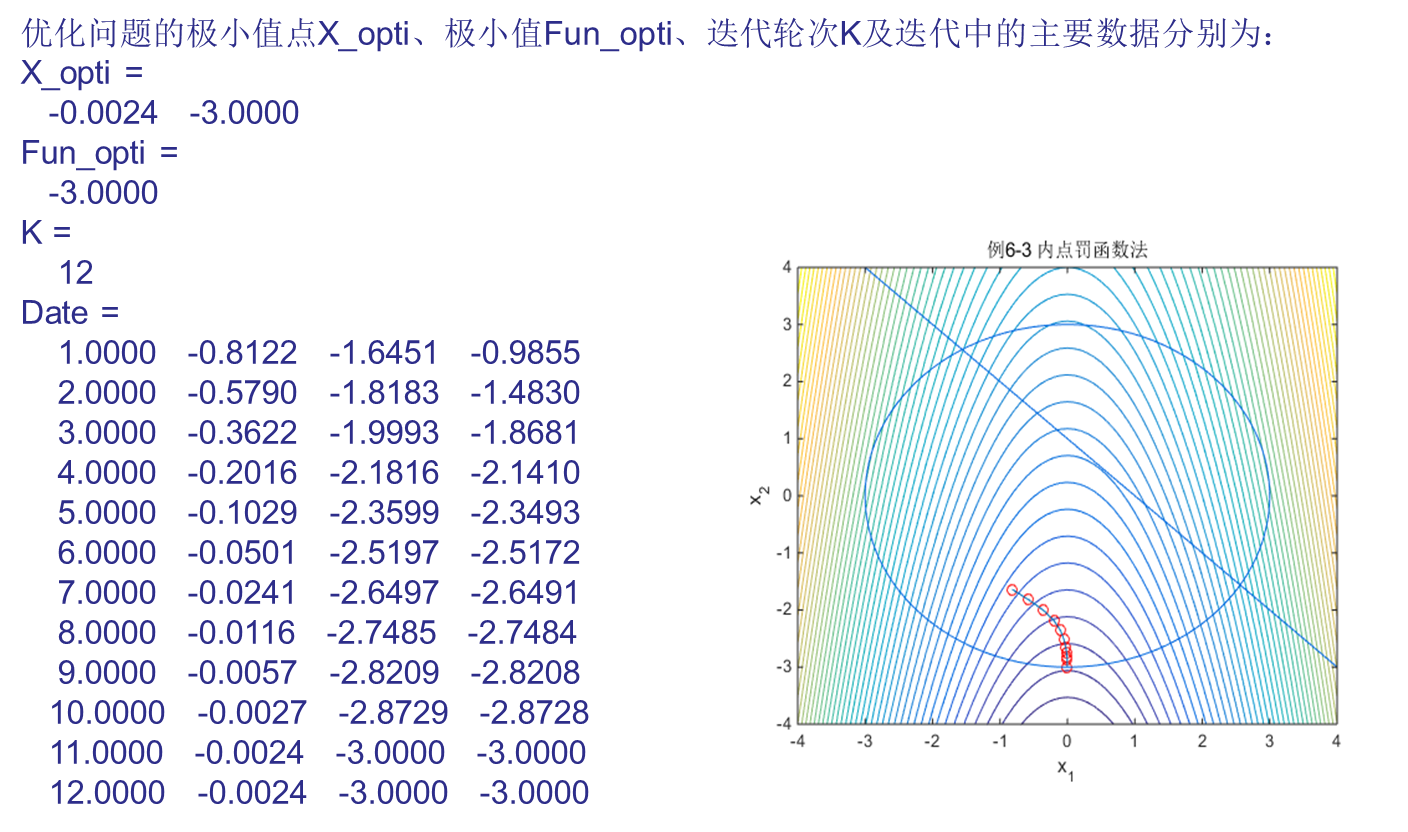



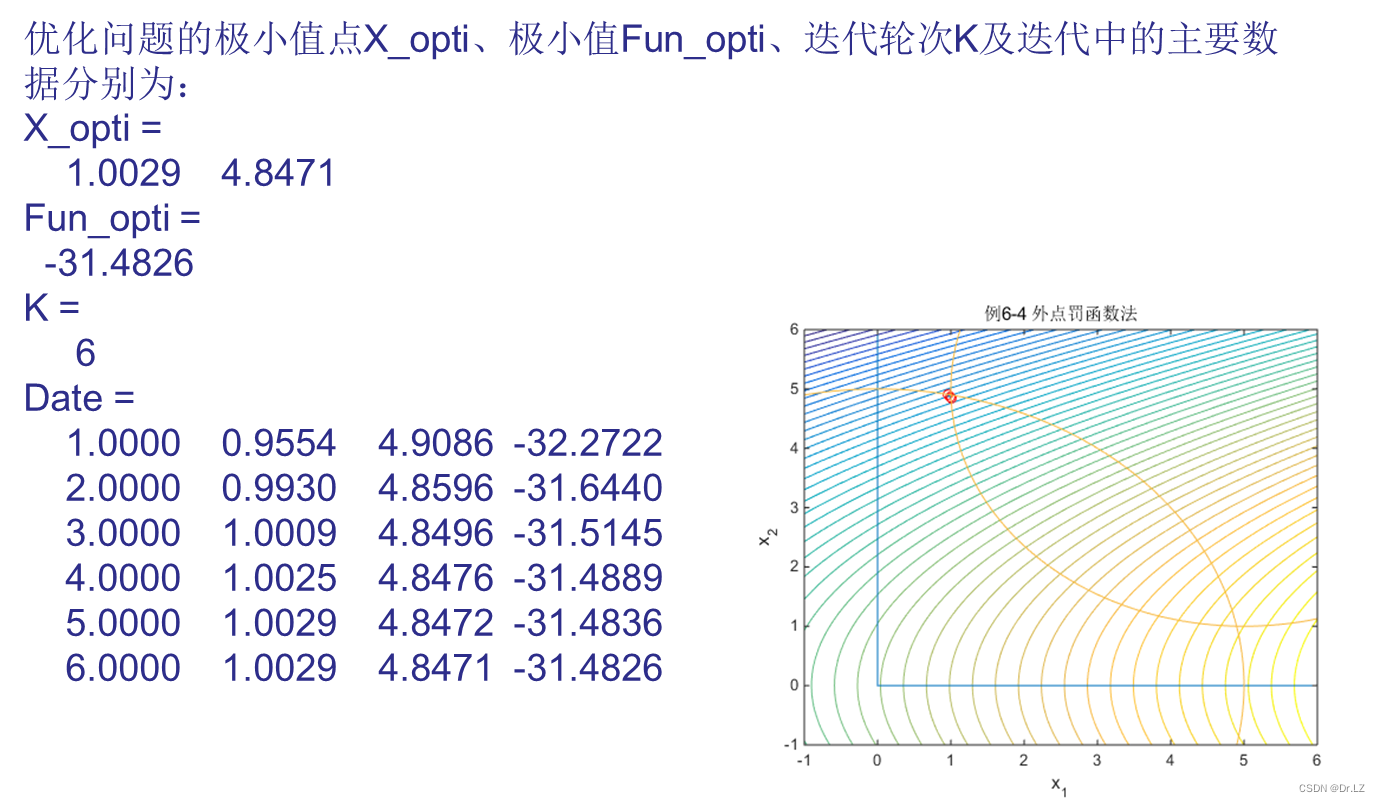
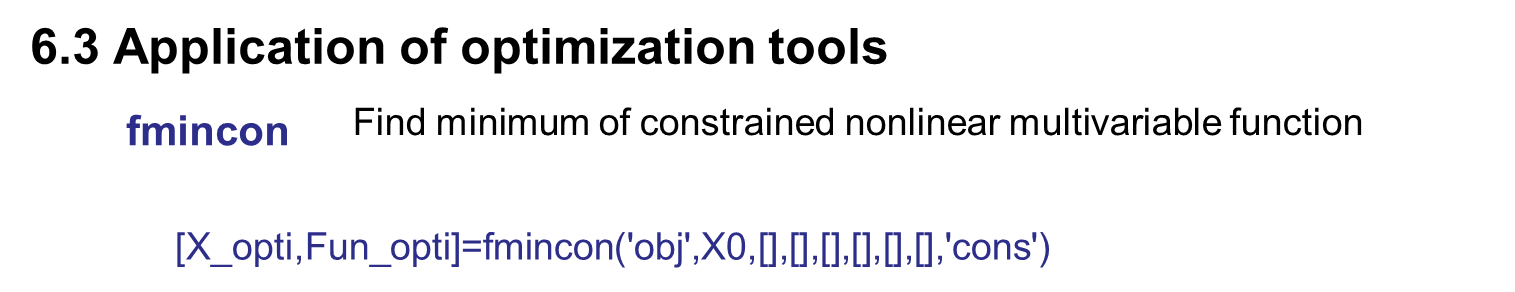
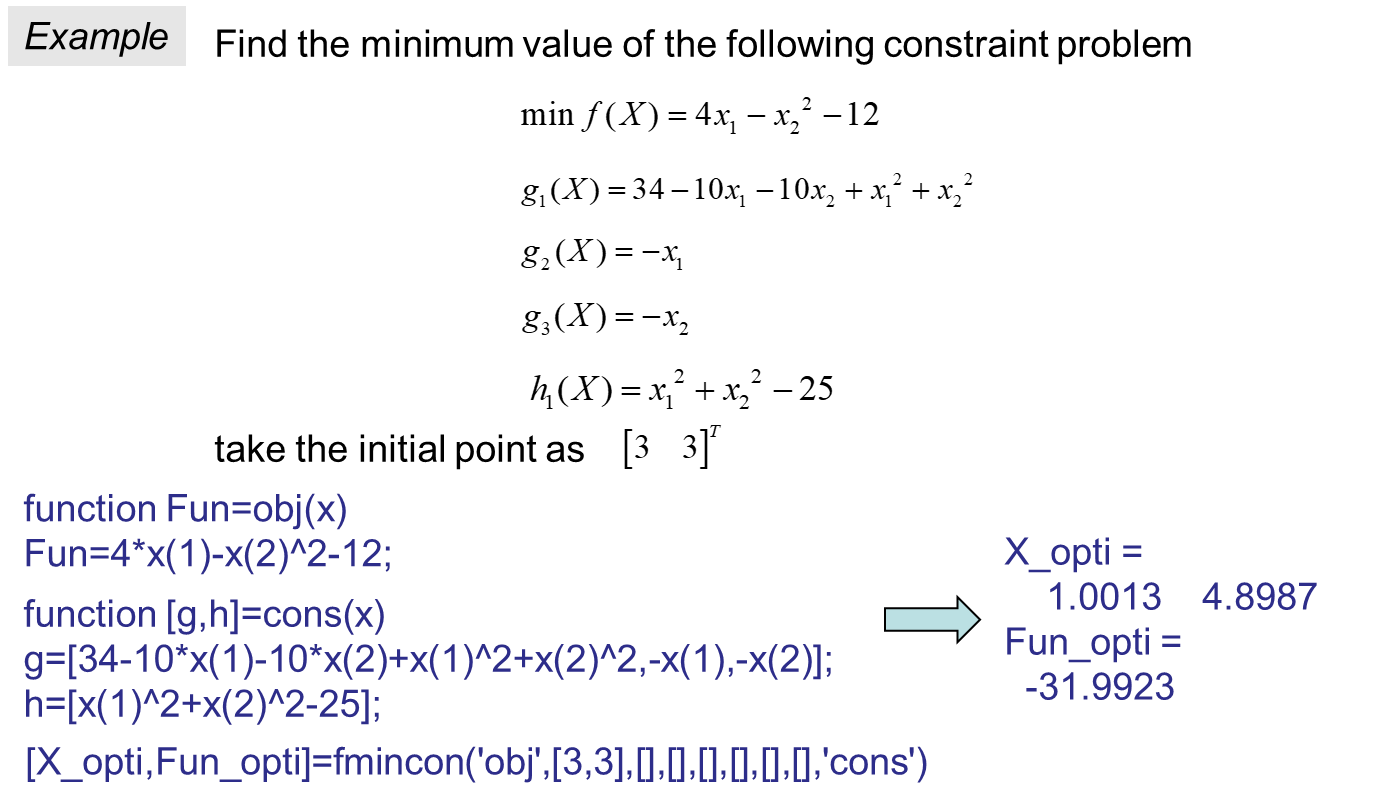
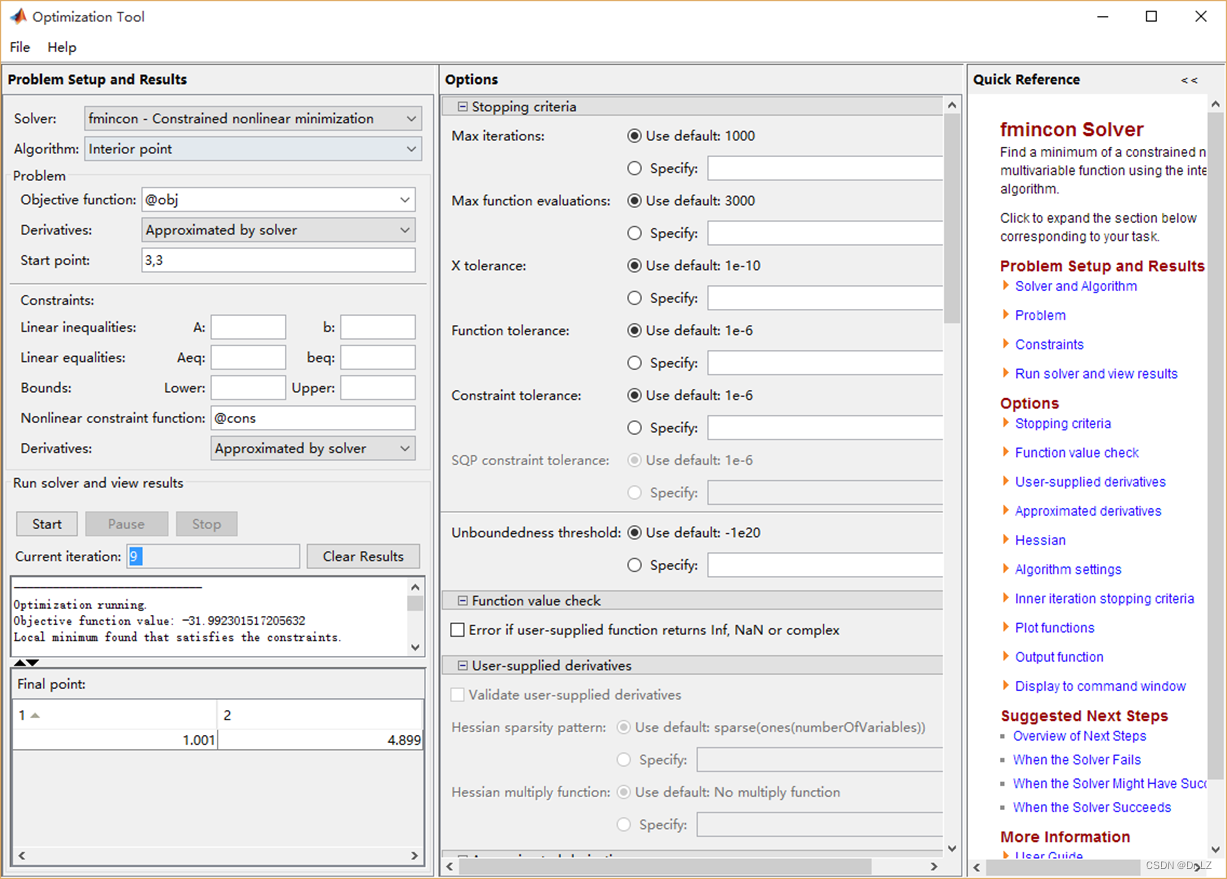
上机实践
最速下降法
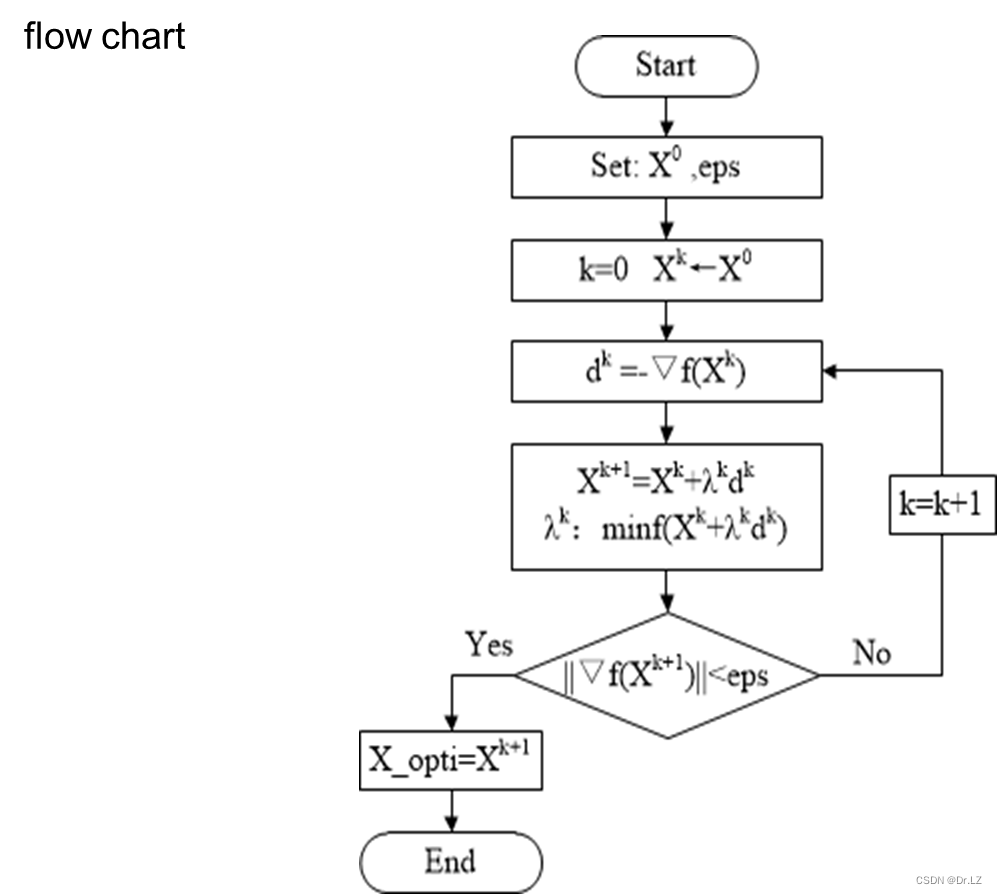
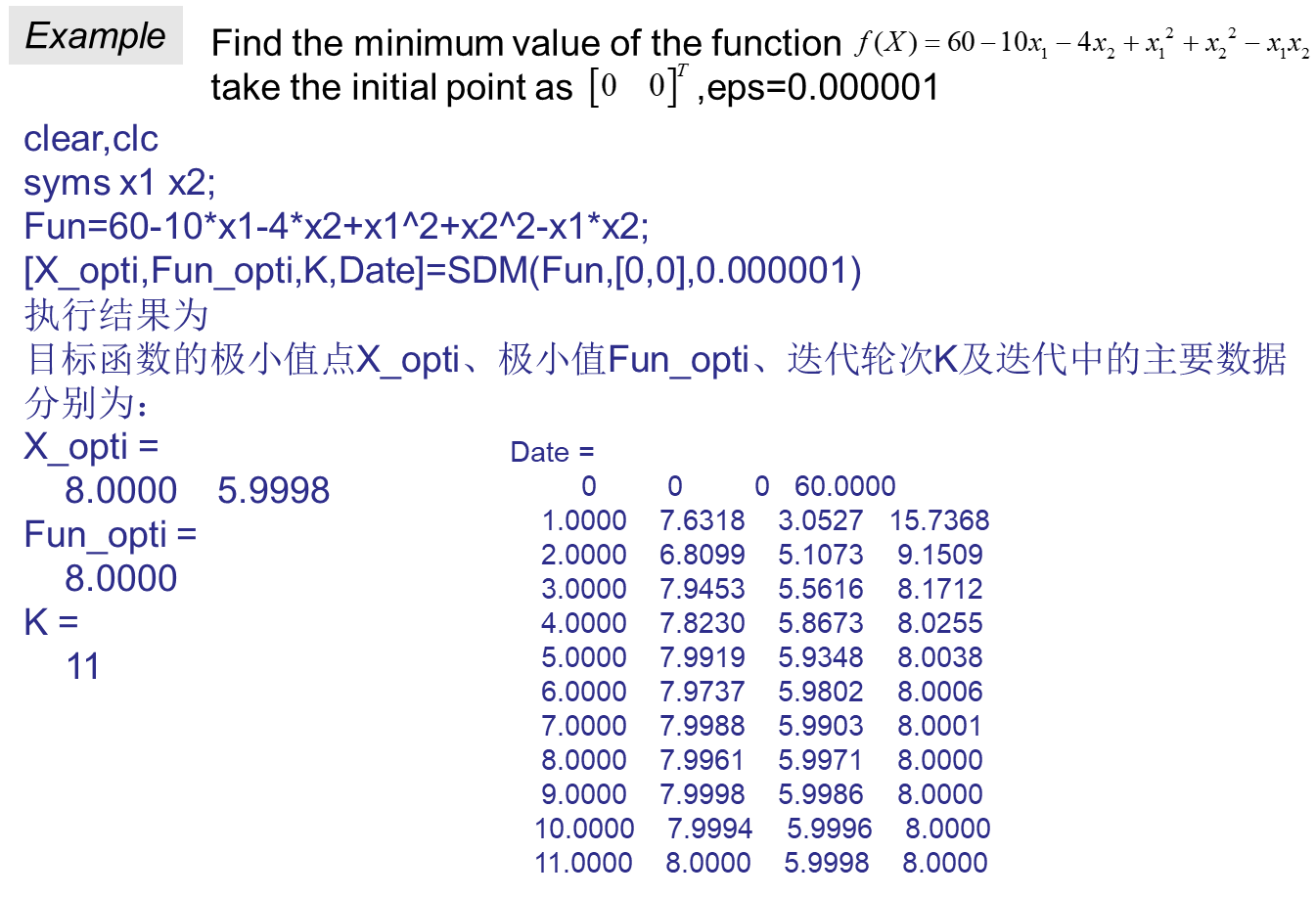
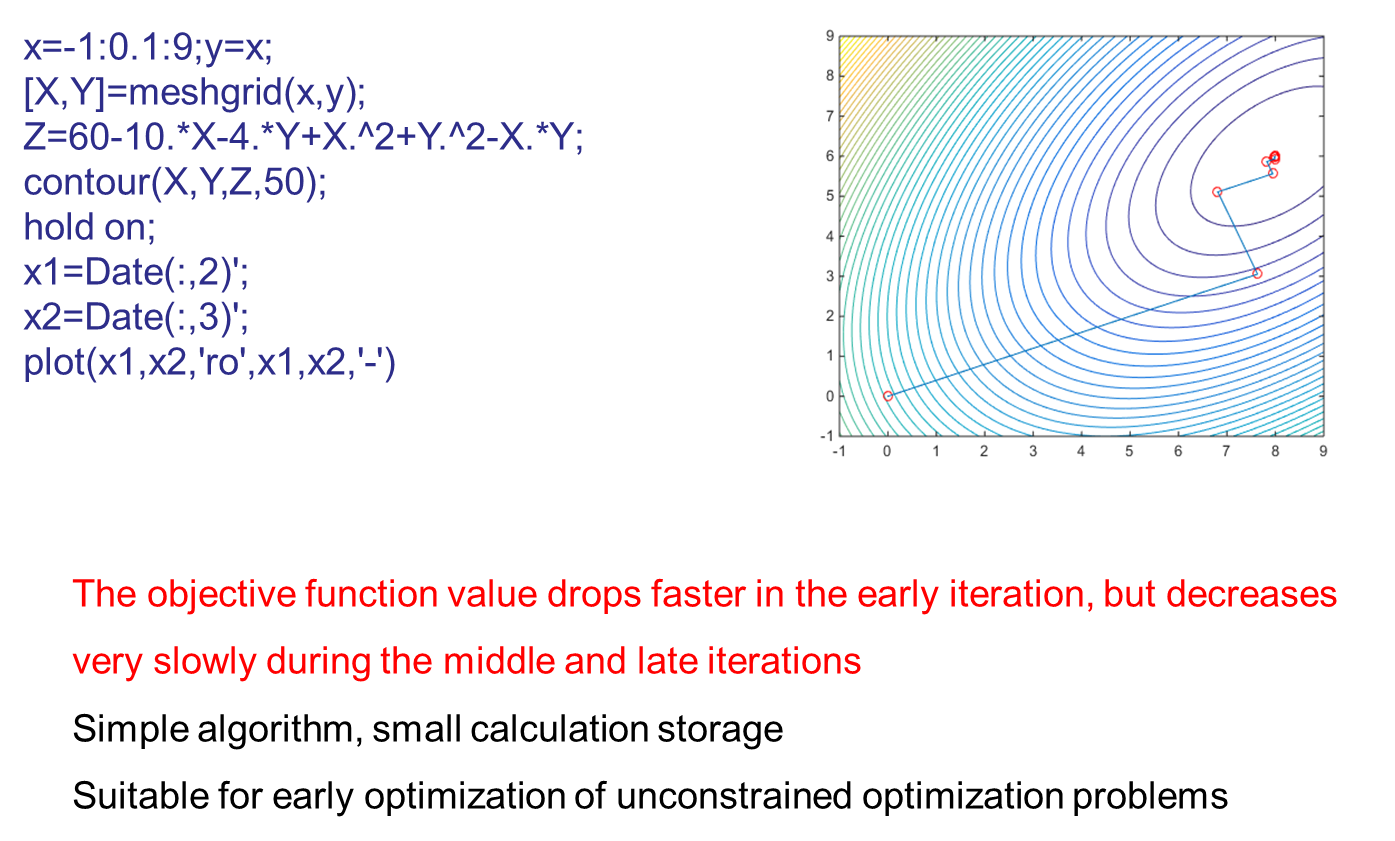
function[X_opti,Fun_opti,K,Date]=SDM(Fun,X0,eps)
%SDM.m Steepest Descent Method(最速下降法:求多维无约束优化问题的极小值),调用格式[X_opti,Fun_opti,K,Date]=SDM(Fun,X0,eps)
%X_opti:极小值点(输出)
%Fun_opti:极小值点处的函数值(输出)
%K:迭代轮次(输出)
%Date:迭代中的主要数据(输出)
%Fun:目标函数(输入),命令窗口中输入格式为:syms x1 x2;Fun=x1^2+25*x2^2
%X0:初始点(输入),命令窗口中输入格式:X0=[2,2]
%eps:收敛精度(输入)
format compact;
format short;
n=length(X0);
Var=sym('x',[1,n]);
Date=zeros(500,n+2);
Grad_exp=jacobian(Fun,Var);
k=0;
syms Iter_step;
Fun_X0=eval(subs(Fun,findsym(Fun),X0));
Grad_X0=subs(Grad_exp,Var,X0);
Date(k+1,1:n+2)=[k,X0,Fun_X0];
Crit=eval(norm(Grad_X0));
if Crit<eps
X_opti=X0;
Fun_opti=Fun_X0;
K=k;
Date(k+2:500,:)=[];
str='输入点为目标函数的极小值点,极小值点X_opti、极小值Fun_opti及迭代轮次K分别为:';
disp(str)
end
while Crit>=eps
Fun_X0=eval(subs(Fun,findsym(Fun),X0));
d=-subs(Grad_exp,Var,X0);
X1_exp=X0+d*Iter_step;
fun=subs(Fun,Var,X1_exp);
[Step_opti]=GSM(fun,0,0.5,0.0001);
X1=eval(subs(X1_exp,Step_opti));
Fun_X1=eval(subs(Fun,findsym(Fun),X1));
k=k+1;
Date(k+1,:)=[k,X1,Fun_X1];
Grad_X1=subs(Grad_exp,Var,X1);
Crit1=eval(norm(Grad_X1));
Crit2=abs(Fun_X1-Fun_X0);
if Crit1<eps||Crit2<eps
X_opti=X1;
Fun_opti=Fun_X1;
K=k;
Date(k+2:500,:)=[]; %
str='目标函数的极小值点X_opti、极小值Fun_opti、迭代轮次K及迭代中的主要数据分别为:';
disp(str)
break;
end
X0=X1;
if k>500
break
end
end
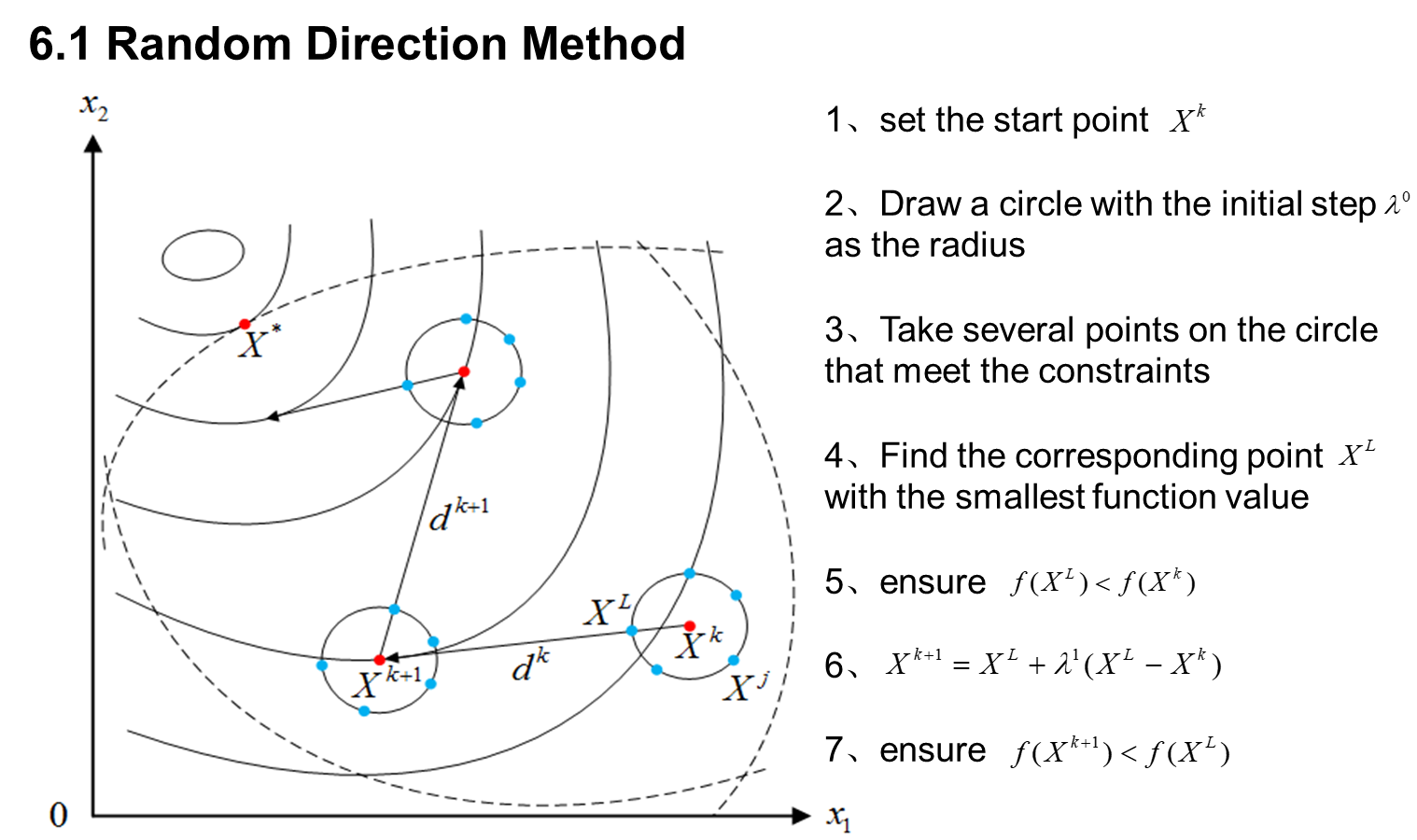
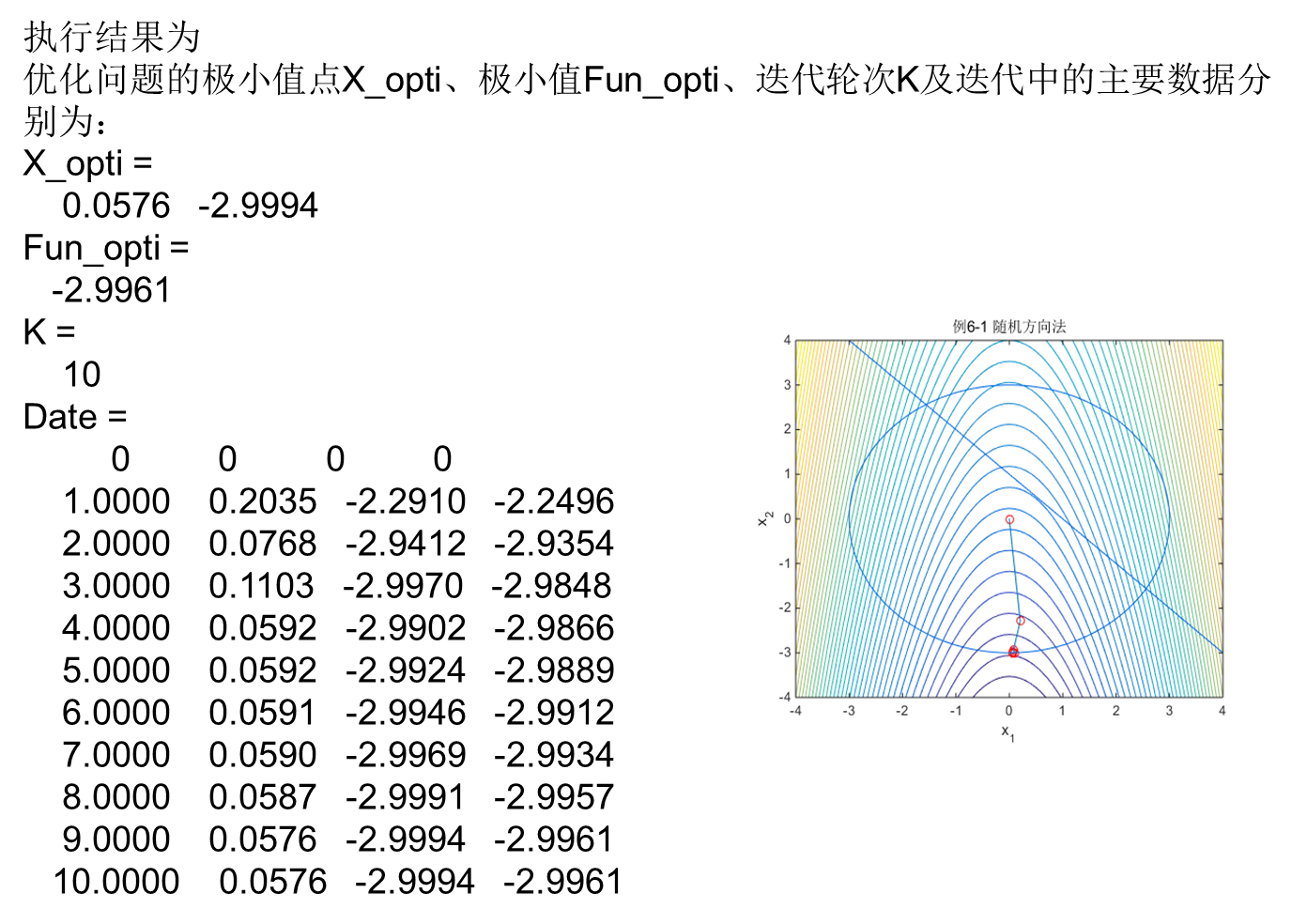
随机方向法
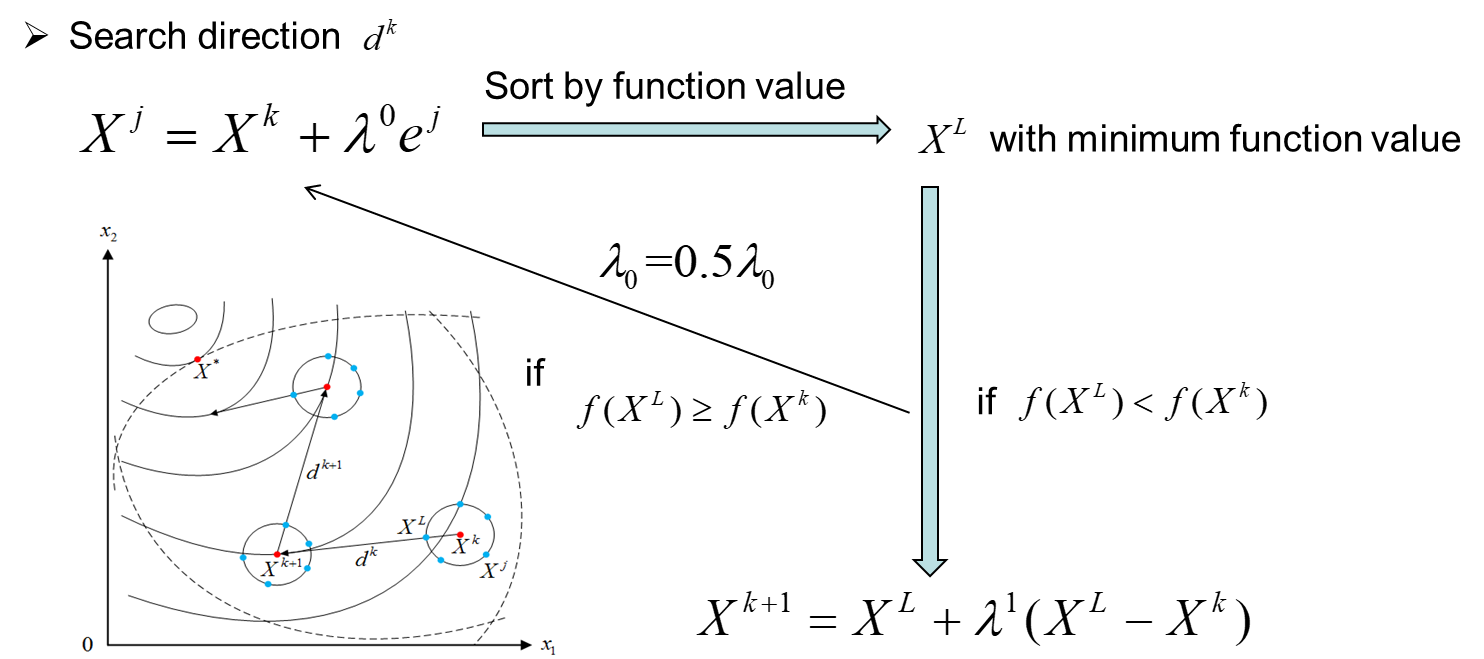
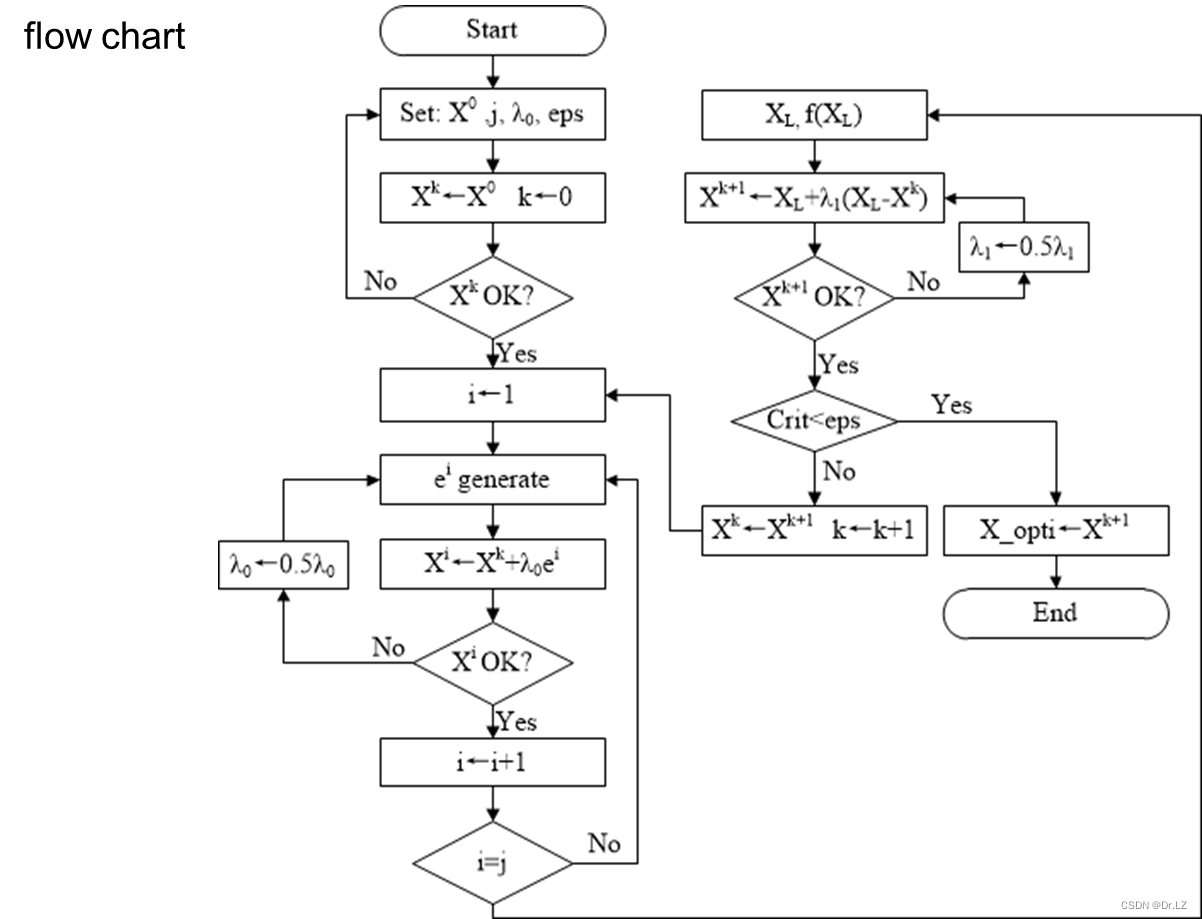
function[X_opti,Fun_opti,K,Date]=RDM(Fun,X0,g,j,step0,eps)
%RDM.m Random Direction Method(随机方向法:求多维不等式约束优化问题的极小值),调用格式[X_opti,Fun_opti,K,Date]=RDM(Fun,X0,g,j,step0,eps)
%X_opti:极小值点(输出)
%Fun_opti:极小值点处的函数值(输出)
%K:迭代轮次(输出)
%Date:迭代中的主要数据(输出)
%Fun:目标函数(输入)
%X0:初始点(输入)
%g:不等式约束(输入),格式小于等于零
%j:随机点个数(输入)
%step0:初始步长(输入)
%eps:收敛精度(输入)
format compact;
format short;
n=length(X0);
Var=sym('x',[1,n]);
m=length(g);
X_val=zeros(j,n);
F_val=zeros(j,1);
g_val=ones(j,m);
Date=zeros(500,n+2);
g_X0=subs(g,Var,X0);
if length(g_X0(g_X0<=0))~=m
str='初始点不可行,请更换初始点';
disp(str)
end
k=0;
kmax=0;
i=1;
Fun_X0=eval(subs(Fun,symvar(Fun),X0));
Date(k+1,1:n+2)=[k,X0,Fun_X0];
while 1
Fun_X0=eval(subs(Fun,symvar(Fun),X0));
while i<=j
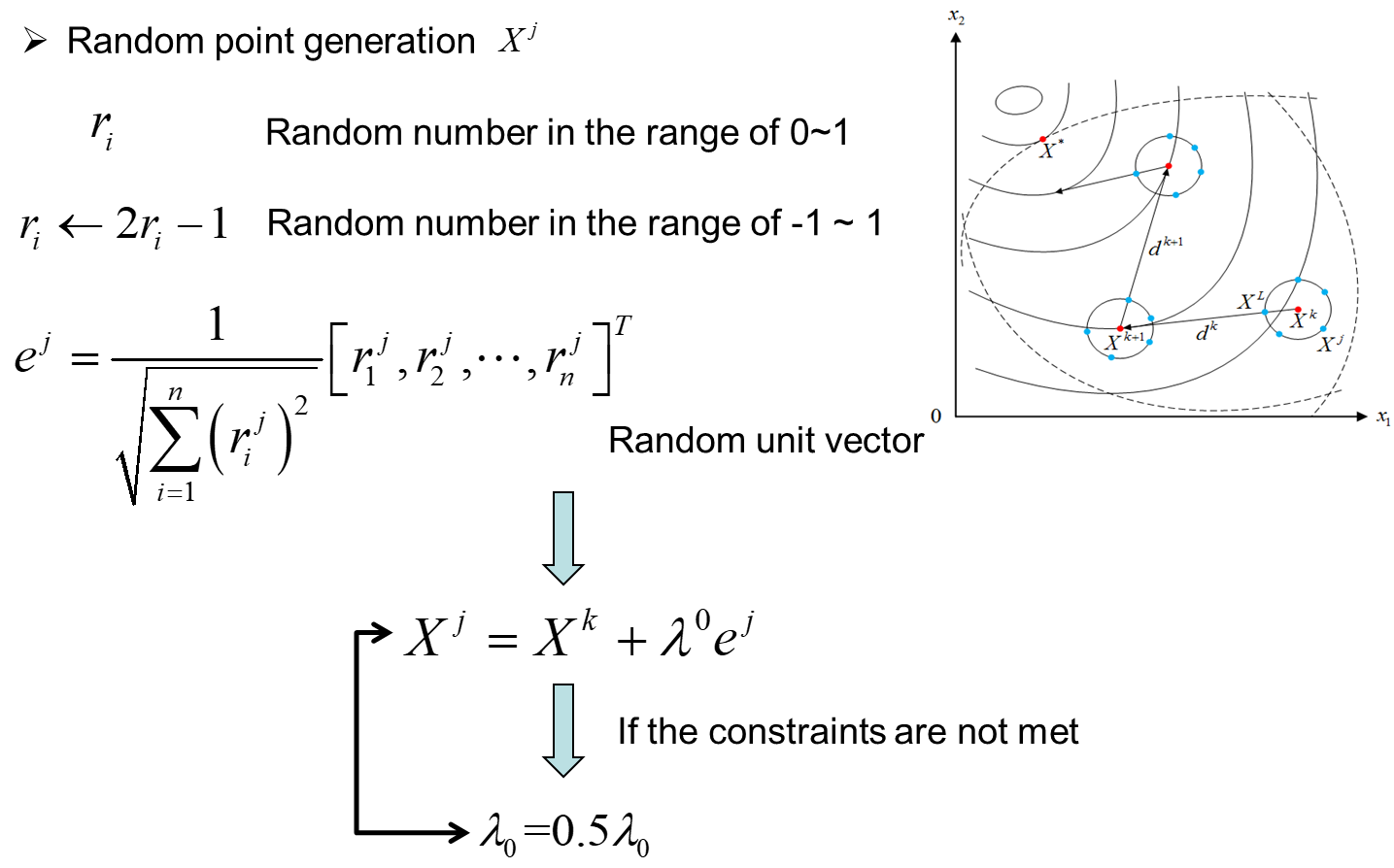
r=2*rand(1,n)-1;
d=(sum(r.^2).^(-0.5)).*r;
X_val(i,:)=X0+step0*d;
F_val(i,:)=eval(subs(Fun,symvar(Fun),X_val(i,:)));
g_val(i,:)=subs(g,Var,X_val(i,:));
kmax=kmax+1;
if length(g_val(g_val(i,:)<=0))~=m
if kmax>=10
step0=0.5*step0;
end
continue
end
i=i+1;
end
i=1;
[sortF,index]=sort(F_val);
sortX=X_val(index,:);
Fun_XL=sortF(1,:);
XL=sortX(1,:);
if Fun_XL>=Fun_X0
step0=0.5*step0;
continue
end
step1=1.3;
X1=XL+step1*(XL-X0);
g_X1=subs(g,Var,X1);
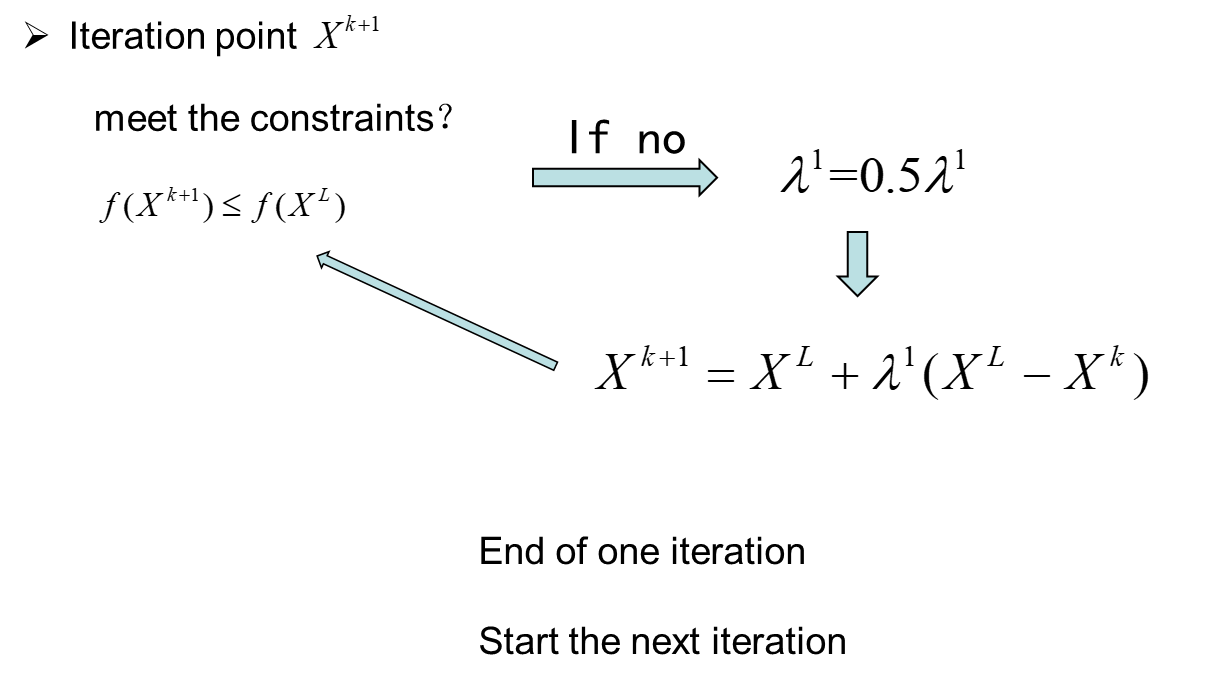
while length(g_X1(g_X1<=0))~=m
step1=0.5*step1;
X1=XL+step1*(XL-X0);
g_X1=subs(g,Var,X1);
end
Fun_X1=eval(subs(Fun,symvar(Fun),X1));
while Fun_X1>=Fun_XL
step1=0.5*step1;
X1=XL+step1*(XL-X0);
Fun_X1=eval(subs(Fun,symvar(Fun),X1));
end
k=k+1;
X0=X1;
Date(k+1,:)=[k,X1,Fun_X1];
Crit=abs(Fun_X1-Fun_X0);
if Crit<eps
X_opti=X1;
Fun_opti=Fun_X1;
K=k;
Date(k+2:500,:)=[];
str='优化问题的极小值点X_opti、极小值Fun_opti、迭代轮次K及迭代中的主要数据分别为:';
disp(str)
break;
end
if k>=100
break
end
end





















 1700
1700

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










