Adaptive linear Element (Adaline)

最新推荐文章于 2024-09-10 20:49:57 发布
最新推荐文章于 2024-09-10 20:49:57 发布
阅读量540 收藏 2
点赞数 1
分类专栏： 神经网络 文章标签： Adaline
原文链接：https://blog.youkuaiyun.com/hallao0/article/details/74858441
版权

1. 初级的神经网络

 单层感知器是用来处理线性可分问题。

线性可分简单的说，如果二维平面上有两类点，然后可以用一条直线一刀切，类似可以扩展到n维。

既然只有两类，就可以用01函数（hardlim）来作为刀，这里叫输出函数，也叫阈值函数。

输入呢有n多，怎么办？sigma（和）一下，就只有一个了。

老是和的话就总是一样的数值了，怎么办？那就加权吧，就是对每个x[i]都有一个特定权值w[i]，然后相乘再相加。

最后弄个偏移量b，多加一个x[0]=1，b=w[0]，这个小技巧就很方便编程了。

模型如下：模型

数学表示：y=hardlim(sigma(w[i]*x[i])) , i=0-n

判决平面：

sigma(w[i]*x[i])=0;

学习算法：

(1) 设置变量和参数：
    X(n)= [1,x1 (n),x2 (n),…,xm (n)]为输入向量；
    W(n)= [b (n),w1 (n),w2 (n),…,wm (n)]为权值向量;
    b (n)为偏差；      y (n)为感知器实际输出；
    d (n)为期望输出； n为迭代次数;
    η为学习速率，对于单层感知器 ，设η =1.
      
(2) 初始化 n=0,权值向量Wj(0)=[各一个较小的随机非零数] 
(3) 对于一组输入样本X(n)，指定它的期望输出y(0|1)      
(4) 计算感知器实际输出 d=hardlim(sigma), e=y[i]-d; 
(5) 调整感知器的权值向量 w[i]new=w[i]old+x[i]*e; 
(6)满足条件？是,结束; 否,n增加1,转第三步。
 
注意：判断满足条件可以是：
        (1) 误差小，即|d(n)-y(n)|<ε ；
        (2) 权值变化小，即|w(n+1)-w(n)|<ε ；
        (3) 超过设定的最大迭代次数。

#include <stdio.h>
#include <time.h>
#include <math.h>
#include <stdlib.h>
 
#define M 4  //样本数
#define N 3  //样本维度
#define Max 10 // 最大次数
#define eps 1e-4
 
inline int hardlim(double a){ return (a>eps)?1:0; }
 
double x[M][N]={
		{1, 0, 0},
		{1, 0, 1},
		{1, 1, 0},
		{1, 1, 1}
};
double y[M]={0,1,1,1};
double w[N];
 
void begin()
{
	int i, j; 
	printf("title: =====ANN==adaline==与门实现=====\n");
	printf("\nbegin: \n");
	printf("	x[0]		x[1]		x[2]		y\n");
	for(i=0; i<M; ++i){
		for(j=0; j<N; ++j){		printf("	%lf", x[i][j]);		}
        printf("	%lf\n", y[i]);
	}
}
 
void train()
{
	int i, j, ok, tim, v;
	double e, d, sigma;
 
	printf("\n\ntrain: \n");
	srand(time(0));
	for(i=0; i<N; ++i){	w[i]=rand()/(RAND_MAX+1.0);	} 
	printf("	e[0]		e[1]		e[2]		e[4]		ok\n");
	tim=0; v=1; // 学习速率
	while(1){
		ok=1;
		for(i=0; i<M; ++i){	
			sigma=0;
			for(j=0; j<N; ++j){	sigma+=x[i][j]*w[j];		}
			d=hardlim(sigma);
			e=y[i]-d;
			
			printf("	%lf ", e);
			if(fabs(e)>eps) ok=0;      //fabs:求绝对值
 
			for(j=0; j<N; ++j){		w[j]+=v*e*x[i][j];		}
		}
		tim++;
		puts(ok?"	Y":"	N");
		if(ok || tim>Max) break;
	}
}
 
void test(){
	int i, j;
	double sigma;
 
	printf("\n\ntest: \n");
	printf("	x[0]		x[1]		x[2]		sigma		ans\n");
	for(i=0; i<M; ++i){
		sigma=0;
		for(j=0; j<N; ++j){
			printf("	%lf", x[i][j]);
			sigma+=x[i][j]*w[j];
		}
		printf("	%lf	", sigma);
		printf("%d\n", hardlim(sigma));
	}
	puts("==end==");
}
 
int main()
{
	begin();
	train();
	test();
	return 0;
}

运行结果:

title: =====ANN==adaline==与门实现=====
 
begin:
        x[0]            x[1]            x[2]            y
        1.000000        0.000000        0.000000        0.000000
        1.000000        0.000000        1.000000        0.000000
        1.000000        1.000000        0.000000        0.000000
        1.000000        1.000000        1.000000        1.000000
 
 
train:
        e[0]            e[1]            e[2]            e[4]            ok
        -1.000000       0.000000        0.000000        0.000000        N
        0.000000        0.000000        0.000000        0.000000        Y
 
 
test:
        x[0]            x[1]            x[2]            sigma           ans
        1.000000        0.000000        0.000000        -0.434174       0
        1.000000        0.000000        1.000000        -0.284882       0
        1.000000        1.000000        0.000000        -0.069977       0
        1.000000        1.000000        1.000000        0.079315        1
==end==
Press any key to continue

2. Adaline

2.1 Adaline原理

一个初级的一层神经网，这是在最初级上面的follow up 版。 
增强的点有： 

1. Bernard新提出了cost function 
2. weights的更新基于线性方程（linear activation function）,而不是之前perceptron中的离散方程（unit step function）

è¿éåå¾çæè¿°

Cost Function
Sum of Square Errors(SSE)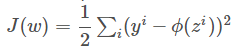 

其中为图中Activation function的输出，在此处简单定义为： 

理想的状况是，目标方程是U型的。我们可以用梯度下降法找到最小的cost.

梯度下降gradient descent

η为步长， 偏导结果为方向 

è¿éåå¾çæè¿°

feature scaling

当η过大时，会发生overshoot. 解决办法一个是减小它的大小，另外一种办法是特征缩放。在此次实验中用的是标准化的方法缩小特征值。

2.2 实现

import numpy as np
class AdalineGD(object):
    """ADAptive LInear NEuron classifier.
    Parameters
    -----------
    eta : float
    Learning rate (between 0.0 and 1.0)
    n_iter : int
    Passes over the training dataset.

    Attributes
    -----------
    w_ : 1d-array
    Weights after fitting.
    errors_ : list
    Number of misclassifications in every epoch.
    """
    def __init__(self, eta=0.01, n_iter=50):
        self.eta = eta
        self.n_iter = n_iter
    def fit(self, X, y):
    """ Fit training data.

    Parameters
    ----------
    X : {array-like}, shape = [n_samples, n_features]
        Training vectors, where n_samples is the number of samples and
        n_features is the number of features.
    y : array-like, shape = [n_samples]Target values.

    Returns
    -------
    self : object
    """
        self.w_ = np.zeros(1 + X.shape[1])
        self.cost_ = []
        for i in range(self.n_iter):
            output = self.net_input(X)
            errors = (y - output)
            #X.T.dot 叉乘 output：向量
            self.w_[1:] += self.eta * X.T.dot(errors)
            self.w_[0] += self.eta * errors.sum()
            cost = (errors**2).sum() / 2.0
            self.cost_.append(cost)
        return self
    def net_input(self, X):
    """Calculate net input"""
        #np.dot 点乘 output:标量
        return np.dot(X, self.w_[1:]) + self.w_[0]
    def activation(self, X):
    """Compute linear activation"""
        return self.net_input(X)
    def predict(self, X):
    """Return class label after unit step"""
        return np.where(self.activation(X) >= 0.0, 1, -1)

重点是weight的更新：

self.w_[1:] += self.eta * X.T.dot(errors)
self.w_[0] += self.eta * errors.sum()

新添的activation function:

def activation(self, X):
    """Compute linear activation"""
    return self.net_input(X)

测试

>>> fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(8, 4))
>>> ada1 = AdalineGD(eta=0.01, n_iter=50).fit(X, y)
>>> ax[0].plot(range(1, len(ada1.cost_) + 1),
... np.log10(ada1.cost_), marker='o')
>>> ax[0].set_xlabel('Epochs')
>>> ax[0].set_ylabel('log(Sum-squared-error)')
>>> ax[0].set_title('Adaline - Learning rate 0.01')
>>> ada2 = AdalineGD(eta=0.0001, n_iter=50).fit(X, y)
>>> ax[1].plot(range(1, len(ada2.cost_) + 1),
... ada2.cost_, marker='o')
>>> ax[1].set_xlabel('Epochs')
>>> ax[1].set_ylabel('Sum-squared-error')
>>> ax[1].set_title('Adaline - Learning rate 0.0001')
>>> plt.show()

è¿éåå¾çæè¿°

左图中，因为learning rate步长太大，发生了overshoot,所以最后没有降下来。 
通过feature scaling, 在此也就是标准化特征：

#减去平均数，除以标准差
>>> X_std = np.copy(X)
>>> X_std[:,0] = (X[:,0] - X[:,0].mean()) / X[:,0].std()
>>> X_std[:,1] = (X[:,1] - X[:,1].mean()) / X[:,1].std()

再将模型fit函数输入改为x_std:

ada.fit(X_std, y)

è¿éåå¾çæè¿°

 

 

 

 

自适应线性神经网络Adaline算法(含完整源码)
DevEnigma的博客
08-24 383
我们定义了一个Adaline类，其中包含了权重向量、学习率等参数。train函数用于训练模型，输入为特征矩阵和标签向量，max_iter表示最大迭代次数，默认为1000。在每次迭代中，随机选择一个样本更新权重向量。自适应线性神经网络Adaline是一种最早被提出的神经网络，它采用连续的激活函数并且引入了代价函数的概念进行最小优化。这里我们将前两类花作为正例，后两类花作为反例，使用Adaline模型进行分类。可以看到，Adaline模型可以对鸢尾花数据集进行较好的分类。，使用当前的权重向量。
C/C++ Adaline自适应线性神经网络算法详解及源码
希望我的博客，能帮上你解决学习中工作中所遇到的问题
06-15 6620
Adaline（自适应线性神经网络）是一种用于二分类任务的线性神经网络算法。它的前身是感知机算法，但与感知机不同的是，Adaline引入了连续的激活函数，使得输出可以是连续的实数值，而不仅仅是二进制值。Adaline的算法基于最小均方误差（MSE）准则进行权重的调整。
ML实践-Adaptive Linear Neurons（Adaline）
hallao0的博客
07-09 932
原理在万事开头难那篇文中，介绍了一个初级的一层神经网，这是在最初级上面的follow up 版。 增强的点有： 1. Bernard新提出了cost function 2. weights的更新基于线性方程（linear activation function），而不是之前perceptron中的离散方程（unit step function）Cost FunctionSum of Squar
线性适应元 - Adaptive Linear Element
u012240857的博客
03-11 958
线性适应元 - Adaptive Linear Element
ANN_Adaptive linear Element (Adaline)
swrdlgc的专栏
10-30 676
人工神经网络就是将生物与计算机结合起来的一种很神的东东。 今天学习了一下单层感知器，它是用来处理线性可分问题的。 线性可分简单的说，如果二维平面上有两类点，然后可以用一条直线一刀切，类似可以扩展到n维。。 既然只有两类，就可以用01函数（hardlim）来作为刀，这里叫输出函数，也叫阈值函数。。 输入呢有n多，怎么办？sigma（和）一下，就只有一个了。。 老是和的话就总
系统学习机器学习之神经网络（八） --ADALINE网络
热门推荐
工作笔记
01-09 1万+
转自：http://www.jianshu.com/p/3c271d59b14c 自适应线性神经网络:ADAptive LInear NEuron (Adaline) 大纲 1. look --- 比Rosenblatt感知器算法的优势 2. write --- 吐槽实验结果 3. code --- python 对比Rosenblatt 憋说话，先上图　-.- Rosen
【神经网络】自适应线性单元——Adaline
Ono_bing的博客
07-05 1420
自适应线性单元–Adaptive Linear Units–Adaline 模型结构 在M-P模型的基础上 s(k)=∑i=1nwixi(k)−θ=∑i=0nwixi(k)=WTX(k)\begin{aligned}s(k)&=\sum_{i=1}^nw_ix_i(k)-\theta\\&=\sum_{i=0}^nw_ix_i(k)\\&=W^TX(k)\end{aligned}s(k)​=i=1∑n​wi​xi​(k)−θ=i=0∑n​wi​xi​(k)=WTX(k)​ y(k)
ADALINE神经网络资源与源程序解析
ADALINE-ANN（Adaptive Linear Element Artificial Neural Network）的概念强调了ADALINE在人工神经网络领域的应用。在ANN中，ADALINE可以看作是最简单的神经网络结构之一。尽管它不能解决非线性问题，但它的训练...
自适应线性元模型(ADALINE)学习解析
"ADALINE模型是自适应线性元模型(Adaptive Linear Element)的缩写，是一种简单的神经网络模型，通常用于分类和回归任务。本资源是国防科大人工神经网络课程的一部分，主要讲解了ADALINE的学习过程。在示例中，通过...
带你了解神经网络自适应线性元件，超级详细的原理以及代码
05-01
自适应线性元件（Adaptive Linear Element，简称Adaline）是一种早期的神经网络模型，由威德罗和霍夫提出。Adaline的主要特征在于其神经元采用线性激活函数，这意味着它的输出可以是连续的任意值，不同于感知器的...
自适应线性元件：LMS学习法则与应用
自适应线性元件（Adaptive Linear Element, Adaline）是早期神经网络模型之一，由威德罗和霍夫在神经科学领域首次提出，旨在解决线性逼近问题和模式联想。与感知器相比，Adaline的主要特点是其神经元使用线性激活...
NN逆模型辨识示例.ppt
11-29
自适应线性神经元，也称为Adaptive Linear Element (ADALINE)，是一种简单的神经网络单元，具有可调权重，能够在线学习和适应环境变化。DTNN则是在离散时间步长上进行计算，更适合于处理实时数据流和控制系统。 在...
pythonML学习笔记ch2-Adaline
Yogurtboyyy的博客
10-16 1137
python机器学习-塞巴斯蒂安.拉施卡学习笔记
神经网络与深度学习实践：利用Adaline算法与Iris数据集实现鸢尾花分类器训练任务
最新发布
2301_76191576的博客
09-10 2111
python初始化类的方法，老生常谈不做解释。
机器学习--自适应神经元Adaline
deek的博客
06-03 683
机器学习–自适应神经元Adaline Adaline规则 感知器优化，规则和感知器相近 Python实现Adaline算法 import numpy as np import matplotlib.pyplot as plt from matplotlib.colors import ListedColormap from sklearn import datasets class AdalineGD(object): def __init__(self, eta=0.01, n_iter=.
Adaline神经网络简单介绍和MATLAB简单实现
记录学习的过程
05-07 8494
Adaline神经网络Adaline利用了最小二乘法的思想，相较于感知机神经网络，对于数据的线性可分的要求更低一些，可以允许一些异常数据。 上面描述了迭代求解的过程，但是在x0(k+1)x_0(k+1)这里没看懂，如果是更新θ\theta应该是w0(k+1)w_0(k+1)才对。应该是PPT有错。 我们来说明下迭代求解需要注意的地方。 首先，将θ\theta并入到ww中去，因为θ\th
使用Adaline神经网络识别印刷体数字
huoji555的博客
04-25 910
1.创建Adaline神经网络 /** * @author Ragty * @param 设置Adaline神经网络 * @serialData 2018.4.24 * @param inputNeuralCount * @param outputNeuralNetwork */ public void creatNetwork(int inputNeuralCount...
C++实现Adaline自适应线性神经网络算法
PixelBlade的博客
09-03 143
Adaline（自适应线性神经网络）是一种经典的神经网络模型，用于解决二分类问题。Adaline算法的核心思想是将输入特征与权重进行线性组合，然后通过激活函数对结果进行判断。然后，我们创建了一个Adaline对象，并使用输入特征和标签进行训练。首先，我们需要定义Adaline类并初始化相关变量，包括学习率（learning rate）和最大迭代次数（maximum iterations）。接下来，我们实现Adaline类的构造函数、激活函数、更新权重函数以及训练和预测函数。
神经网络模型分类
xyjikl
12-08 9695
本文主要介绍一下几种不同类型的神经网络模型，主要有前馈神经网络，反馈神经网络，自组织神经网络，随机神经网络 1.前馈神经网络 1)自适应线性神经网络(Adaline) 自适应线性神经网络（Adaptive Linear，简称Adaline) 是由威德罗（Widrow）和霍夫（Hoff）首先提出的。它与感知器的主要不同之处在于其神经元有一个线性激活函数，这允许输出可以是任意值，而不仅仅只是像感
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值