kari433 矩阵快速幂_矩阵433题-优快云博客

本文链接：https://blog.youkuaiyun.com/smilewsw/article/details/38407047

时间限制 1000 ms 内存限制 65536 KB

题目描述

已知函数f,f(0)=f(1)=1,对于所有n>=2，f(n)=f(n-1)+f(n-2)+n。给定n，求f(n)。

输入格式

第一行一个整数t,表示组数,t<1000。之后t行每行一个整数n,0<=n<=1e9。

输出格式

对于每组测试组，输出一行f(n)%1000000007.

输入样例

输出样例

类似的题通过公式叠加，消去一些项，得到一个仅关于f()之间的递推式，转化成矩阵乘法，迭代计算。

该题：f(n)=3f(n-1)-2f(n-2)-f(n-3)+f(n-4)

对应矩阵为：3 -2 -1 1 # 1 0 0 0 # 0 1 0 0 # 0 0 1 0。然后利用快速幂计算。注意取模为负数的情况，先%MOD再+MOD再%MOD。

代码：#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<queue>
#include<stack>
using namespace std;
struct matrix
{
    long long m[10][10];
};
matrix mul(matrix a,matrix b)
{
    int i,j,k;
    matrix c;
    memset(c.m,0,sizeof(c.m));
    for(i=0;i<4;i++)
    {
        for(j=0;j<4;j++)
        {
            for(k=0;k<4;k++)
                c.m[i][j]=(c.m[i][j]+a.m[i][k]*b.m[k][j])%1000000007;
        }
    }
    return c;
}
matrix qmul(matrix a,int n)
{
    matrix c,orign=a;
    memset(c.m,0,sizeof(c.m));
    for(int i=0;i<4;i++)
        c.m[i][i]=1;
    while(n)
    {
        if(n&1)
            c=mul(c,orign);
        orign=mul(orign,orign);
        n>>=1;
    }
    return c;
}
int main()
{
    matrix a;
    long long sum;
    memset(a.m,0,sizeof(a.m));
    a.m[0][0]=3; a.m[0][1]=-2; a.m[0][2]=-1; a.m[0][3]=1;
    a.m[1][0]=a.m[2][1]=a.m[3][2]=1;
    int n,t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        if(n==0||n==1)
            printf("1\n");
        else if(n==2)
            printf("4\n");
        else if(n==3)
            printf("8\n");
        else
        {
            matrix c=qmul(a,n-3);
            sum=((c.m[0][0]*8+c.m[0][1]*4+c.m[0][2]+c.m[0][3])%1000000007+1000000007)%1000000007;;
            printf("%lld\n",sum);
        }
    }
    return 0;
}

另一题：So Easy!
Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2201    Accepted Submission(s): 685



   
   
    
    Problem Description
   
   
   
   
    
    　　A sequence S
    
    _n is defined as:

    
    
     
     
    
    
Where a, b, n, m are positive integers.┌x┐is the ceil of x. For example, ┌3.14┐=4. You are to calculate S
    
    _n.
　　You, a top coder, say: So easy!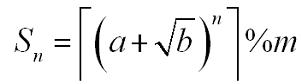 

    
    
     
     
    
    
   
   
   
   
    
     
   
   


   
   
    
    Input
   
   
   
   
    
    　　There are several test cases, each test case in one line contains four positive integers: a, b, n, m. Where 0< a, m < 2
    
    ¹⁵, (a-1)
    
    ²< b < a
    
    ², 0 < b, n < 2
    
    ³¹.The input will finish with the end of file.
   
   
   
   
    
     
   
   


   
   
    
    Output
   
   
   
   
    
    　　For each the case, output an integer S
    
    _n.
   
   
   
   
    
     
   
   


   
   
    
    Sample Input
   
   
   
   
    
         
     
      
      2 3 1 2013
2 3 2 2013
2 2 1 2013
     
     
   
   
   
   
    
     
   
   


   
   
    
    Sample Output
   
   
   
   
    
         
     
      
      4
14
4
     
     
   
   
   
   
    
     
   
   


   
   
    
    Source
   
   
   
   
    
    2013 ACM-ICPC长沙赛区全国邀请赛——题目重现
   
   
   
   
    
    记(a+b√)n为An，配项
    
    Cn=An+Bn=(a+b√)n+(a−b√)n
    
    两项恰好共轭，所以Cn是整数。又根据限制条件
    
    (a−1)2<b<a2⇒0<a−b√<1⇒0<(a−b√)n<1⇒Bn<1
    
    也就是说Cn=⌈An⌉
    
    Sn=(Cn)%m
    
    求Cn的方法是递推。 对Cn乘以(a+b√)+(a−b√)
    
    Cn[(a+b√)+(a−b√)]=[(a+b√)n+(a−b√)n][(a+b√)+(a−b√)]=(a+b√)n+1+(a−b√)n+1+(a+b√)n(a−b√)+(a−b√)n(a+b√)=Cn+1+(a2−b)(a+b√)n−1+(a2−b)(a−b√)n−1=Cn+1+(a2−b)Cn−1
    
    于是
    
    
    
    

   
   
   
   
    
    

   
   
   
   
    
    代码：
    
    #include<stdio.h>
#include<stdio.h>
#include<math.h>
//公式变换和矩阵快速幂 
struct matrix
{
	long long  a[2][2];
} origin,res;
typedef struct matrix MATRIX;
long long m;
MATRIX multiply(MATRIX x,MATRIX y)
{
	MATRIX temp;
	int i,j,k;
	for(i=0;i<2;i++)
		for(j=0;j<2;j++)
			temp.a[i][j]=0;
	for(i=0;i<2;i++)
	{
		for(j=0;j<2;j++)
		{
			for(k=0;k<2;k++)
				temp.a[i][j]=(temp.a[i][j]+x.a[i][k]*y.a[k][j])%m;
		}
	}
	return temp;
}

void calc(int n)
{
	while(n)
	{
		if(n&1)
			res=multiply(res,origin);
		n>>=1;
		origin=multiply(origin,origin);
	} 
}

main()
{
	long long i,j,a,b,n;
	while(scanf("%I64d %I64d %I64d %I64d",&a,&b,&n,&m)!=EOF)
	{
		for(i=0;i<2;i++)
			for(j=0;j<2;j++)
				res.a[i][j]=0;
		res.a[0][0]=res.a[1][1]=1;
		origin.a[0][0]=2*a;
		origin.a[0][1]=-(a*a-b);
		origin.a[1][0]=1;
		origin.a[1][1]=0;
		calc(n);
		printf("%I64d\n",((res.a[1][0]*2*a+res.a[1][1]*2)%m+m)%m);
	}
	return 0;
}