【优化算法】多维粒子群优化算法步骤及matlab实现

粒子群优化算法

粒子群算法，也称粒子群优化算法或鸟群觅食算法（Particle Swarm Optimization）缩写为 PSO。
粒子群优化算法是一种进化计算技术（evolutionary computation），1995 年由 Eberhart 博士和 kennedy 博士提出，源于对鸟群捕食的行为研究。
该算法最初是受到飞鸟集群活动的规律性启发，进而利用群体智能建立的一个简化模型。粒子群算法在对动物集群活动行为观察基础上，利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得最优解。

1.算法步骤

分步说明：

1. 开始

   • 启动算法流程。

2. 初始化粒子群

   • 设定参数：粒子数量 $N$、惯性权重 $\omega （控制历史速度影响）$、学习因子 $c_1（个体认知）,c_2（社会协作）$、最大迭代次数等。
   • 随机生成每个粒子的初始位置 $x_i$ 和速度 $v_i$，确保在解空间范围内。
   • 初始化每个粒子的个体最优位置 $p_{best}^i=x_i$​，全局最优位置 $g_{best}^i$​ 设为当前最优解。
   • 意义：通过随机分布粒子，覆盖解空间的不同区域，为后续搜索提供多样性。

3. 评估粒子适应度

   • 计算每个粒子当前位置的目标函数值 $f(x_i)$，即适应度值（即函数值）。
   • 意义：量化每个粒子当前位置的优劣，适应度值决定了粒子的优劣，是后续更新个体和全局最优的依据。

4. 更新个体最优 $p_{best}$ 和全局最优 $g_{best}$

   • 个体最优：若当前适应度优于该粒子的历史最优值，即当前适应度 $f(x_i)$ 优于 $f(p_{best}^i)$，则更新 $p_{best}^i=x_i$​。
   • 全局最优：从所有粒子的个体最优中，选择适应度最好的位置，即所有 $p_{best}^i$ 中选择最优解，更新 $g_{best}$。
   • 意义：$p_{best}$ 代表粒子的“个体经验”，引导其向自身曾发现的最优位置移动；$g_{best}$ 代表“群体经验”，引导所有粒子向群体最优位置收敛。

5. 更新速度和位置
   按以下公式更新每个粒子：

   • 速度更新：
     $v_i^{t+1}=\omega \cdot v_i^t+c_1\cdot r_1\cdot (p_{best}^i-x_i^t)+c_2\cdot r_2\cdot (g_{best}^i-x_i^t)$，其中 $r_1,r_2$ 为 [0,1] 的随机数。
     惯性项 $\omega \cdot v_i^t$：维持原有运动方向，避免突变。
     认知项 $c_1\cdot r_1\cdot (p_{best}^i-x_i^t)$：向个体历史最优方向移动，保持多样性。
     社会项 $c_2\cdot r_2\cdot (g_{best}^i-x_i^t)$：向群体最优方向移动，加速收敛。
   • 位置更新：
     $x_i^{t+1}=x_i^t+v_i^{t+1}$
   • 边界处理：若位置超出范围，可截断或反射至边界（如 $x_i=max(min(x_i,20),5)$）。
   • 意义：速度更新平衡了“探索”（全局搜索）和“开发”（局部精细搜索）；位置更新使粒子在解空间中移动，逐步逼近最优解。

6. 检查终止条件
   常见终止条件包括：

   • 达到最大迭代次数。
   • 全局最优适应度变化小于阈值（如 $|f(g_{best}^t)-f(g_{best}^{t-1})|<ϵ$）。
   • 解的质量满足要求。
   • 意义：在计算资源有限的情况下，确保算法高效终止，避免无限循环。

7. 输出最优解

   • 返回全局最优位置 $g_{best}$ 及其适应度 $f(g_{best})$。

2.参数选择

(1)惯性权重 $\omega$

惯性权重 $\omega$ 表示粒子保留上一时刻速度的比例，类似于物理中的惯性。它决定了粒子对原有运动方向的依赖程度。作用：

• 全局探索（Exploration）：较大的 w（如 w>0.8）使粒子保持较高的运动速度，能够探索更广的解空间，避免过早陷入局部最优。
• 局部开发（Exploitation）： 较小的 w（如 w<0.4）使粒子速度减慢，便于在潜在最优区域进行精细搜索。

动态调整策略：实际应用中常采用线性递减策略，例如：其中 $t$ 是当前迭代次数，$T_{max}$​ 是最大迭代次数。初始阶段 $\omega$ 较大（如 0.9）以增强全局搜索，后期逐渐减小（如 0.4）以提升局部开发。典型取值范围：

• 固定值：$0.4\le \omega \le 0.9$；
• 动态调整：$\omega$ 从 0.9 线性递减至 0.4。

(2)个体学习因子 $c_1$

个体学习因子（Cognitive Coefficient）控制粒子向自身历史最优位置（$p_{best}$）移动的倾向，反映粒子的“自我认知”能力。典型取值范围：1.5≤c1≤2.0。作用：

• 多样性维护： 较大的 $c_1$​ 会强化粒子对自身经验的依赖，使粒子更倾向于向自己曾找到的最优位置移动，增加群体多样性，避免早熟收敛。
• 局部搜索： 若 $c_1$​ 过高（如 $c_1>2.5$），可能导致粒子过度关注自身经验，忽略群体协作，导致搜索效率下降。

(3) 社会学习因子 $c_2$

社会学习因子（Social Coefficient）控制粒子向群体历史最优位置（$g_{best}$）移动的倾向，反映粒子的“社会协作”能力。典型取值范围：1.5≤c1≤2.0。作用：

• 快速收敛： 较大的 $c_2$ 会强化粒子对群体经验的依赖，使粒子更快向全局最优位置聚集，加速收敛。
• 早熟收敛风险： 若 $c_2$​ 过高（如 $c_2>2.5$），可能导致粒子过早聚集到某个局部最优解，失去探索其他区域的机会。

(4) 参数设置建议

参数名称	作用场景	推荐值或策略
惯性权重 $\omega$	需要全局搜索时（如初期迭代）	初始 $\omega =0.9$，线性递减至 $\omega =0.4$
	需要局部开发时（如后期迭代）	固定 $\omega =0.4—0.6$
个体学习因子 $c_1$	解空间复杂、多峰问题时（需保持多样性）	$c_1=2.0$
社会学习因子 $c_2$​	解空间平滑、单峰问题时（需快速收敛）	$c_2=2.0$
平衡模式	一般问题（平衡探索与开发）	$c_1=c_2=1.5—2.0$

参数影响示例：

• 示例1：全局探索不足（$\omega$ 过小，$c_2$ 过大），粒子迅速聚集到某个局部最优解，无法跳出，导致早熟收敛。
• 示例2：局部开发不足（$\omega$ 过大，$c_2$ 过大），粒子在解空间中随机游走，无法收敛到最优解。
• 示例3：平衡模式（$\omega$ 动态调整，$c_1=c_2=2.0$），初期广泛搜索，后期精细开发，兼顾全局探索与局部收敛。

3. MATLAB 实现

以以下函数为例：
$$f(x_i)=\sum _{i=1}^5(x_i-10{)}^2$$

%% PSO算法求解多维函数最小值（带动态雷达图可视化）
% 目标函数：f(x) = sum((x-10)^2), 搜索范围：x∈[5,20]^5
clc; clear; close all;

%% ====================== 算法参数设置 ======================
nParticles = 10;      % 粒子数量 (建议范围：20-50)
maxIter = 1000;       % 最大迭代次数 (建议范围：500-2000)
w = 0.6;              % 惯性权重 (建议范围：0.4-0.9)
c1 = 1.7;             % 个体学习因子 (建议范围：1.5-2.0)
c2 = 1.7;             % 社会学习因子 (建议范围：1.5-2.0)
dim = 5;              % 问题维度（5维空间）
lb = 5 * ones(1,dim); % 变量下界 [5,5,5,5,5]
ub = 20 * ones(1,dim);% 变量上界 [20,20,20,20,20]
tol = 1e-6;           % 收敛阈值 (适应度差异<tol时停止)

%% ==================== 初始化粒子群 ====================
% 粒子结构体定义：
%   position    - 当前位置
%   velocity    - 当前速度
%   best_pos    - 个体历史最优位置
%   best_fitness- 个体历史最优适应度
particles = repmat(struct(...
    'position', [], ...
    'velocity', [], ...
    'best_pos', [], ...
    'best_fitness', inf), nParticles, 1);

% 随机初始化粒子
for i = 1:nParticles
    particles(i).position = lb + (ub - lb).*rand(1,dim); % 均匀分布初始化
    particles(i).velocity = zeros(1,dim);                 % 初始速度为0
    particles(i).best_pos = particles(i).position;       % 初始化个体最优
end

% 全局最优初始化
global_best_fitness = inf;
global_best_pos = [];
data_global_best_pos = []; % 存储全局最优历史记录

%% ===================== 目标函数定义 =====================
objective_func = @(x) sum((x - 10).^2); % 示例函数：逼近10的平方和

%% ====================== 首次评估 =======================
for i = 1:nParticles
    current_fitness = objective_func(particles(i).position);
    
    % 更新个体最优
    if current_fitness < particles(i).best_fitness
        particles(i).best_fitness = current_fitness;
        particles(i).best_pos = particles(i).position;
    end
    
    % 更新全局最优
    if current_fitness < global_best_fitness
        global_best_fitness = current_fitness;
        global_best_pos = particles(i).position;
    end
end
data_global_best_pos = [data_global_best_pos; global_best_pos]; % 记录初始最优

%% ====================== 主循环 ========================
for iter = 1:maxIter
    % 速度位置更新
    for i = 1:nParticles
        % 计算随机因子
        r1 = rand(1,dim);
        r2 = rand(1,dim);
        
        % 速度更新公式：v = w*v + c1*r1*(pbest - x) + c2*r2*(gbest - x)
        cognitive = c1 * r1 .* (particles(i).best_pos - particles(i).position);
        social = c2 * r2 .* (global_best_pos - particles(i).position);
        particles(i).velocity = w * particles(i).velocity + cognitive + social;
        
        % 位置更新并限制边界
        particles(i).position = particles(i).position + particles(i).velocity;
        particles(i).position = max(min(particles(i).position, ub), lb); % 夹逼处理
        
        % 计算新适应度
        current_fitness = objective_func(particles(i).position);
        
        % 更新个体最优
        if current_fitness < particles(i).best_fitness
            particles(i).best_fitness = current_fitness;
            particles(i).best_pos = particles(i).position;
        end
        
        % 更新全局最优
        if current_fitness < global_best_fitness
            global_best_fitness = current_fitness;
            global_best_pos = particles(i).position;
        end
    end
    
    % 记录全局最优变化（仅在更新时记录）
    if ~isequal(global_best_pos, data_global_best_pos(end,:))
        data_global_best_pos = [data_global_best_pos; global_best_pos];
    end
    
    % 显示迭代信息
    if mod(iter, 50) == 0
        fprintf('Iter %4d | Best Fit: %.4e | Pos: ', iter, global_best_fitness);
        fprintf('%.2f ', global_best_pos);
        fprintf('\n');
    end
    
    % 收敛判断（检查所有粒子最优适应度差异）
    all_fitness = [particles.best_fitness];
    if (max(all_fitness) - min(all_fitness)) < tol
        fprintf('Early stopping at iteration %d\n', iter);
        break;
    end
end

%% ===================== 结果显示 ======================
fprintf('\n=== 优化结果 ===\n');
fprintf('最优解: [');
fprintf('%.4f ', global_best_pos);
fprintf(']\n');
fprintf('最优适应度: %.4e\n', global_best_fitness);

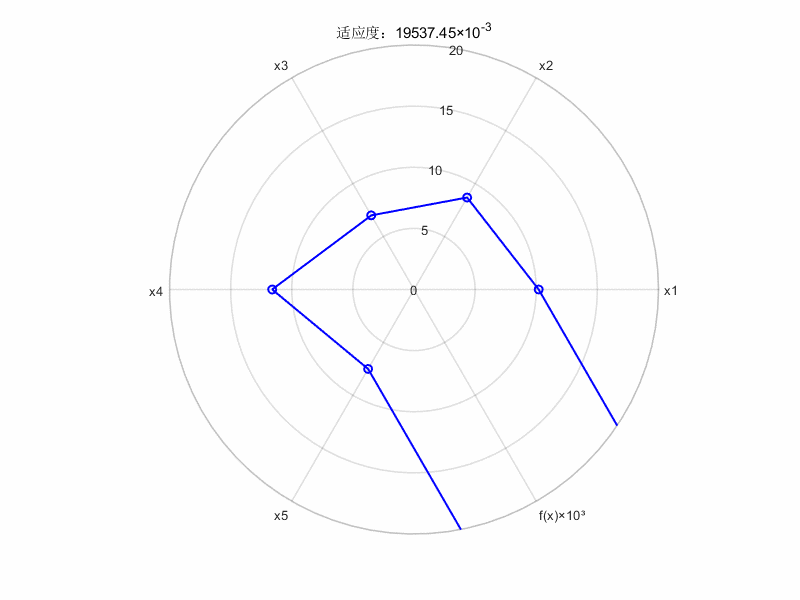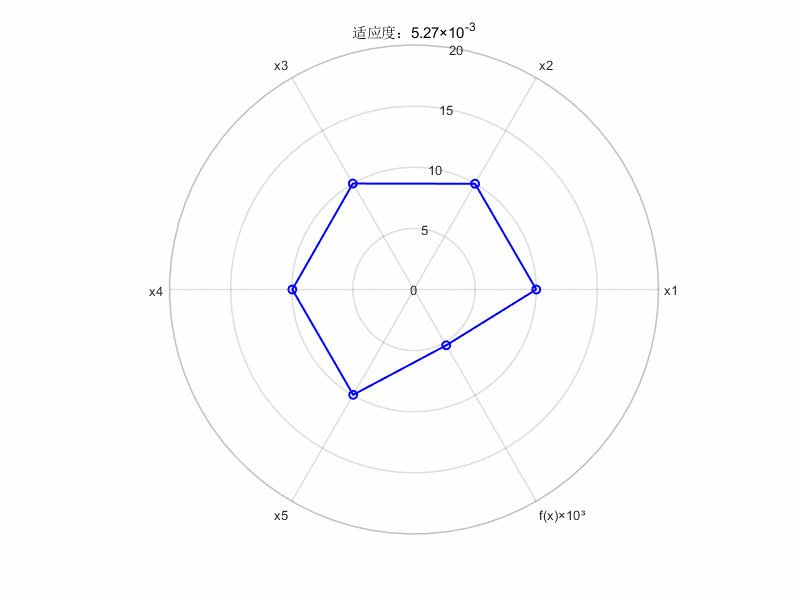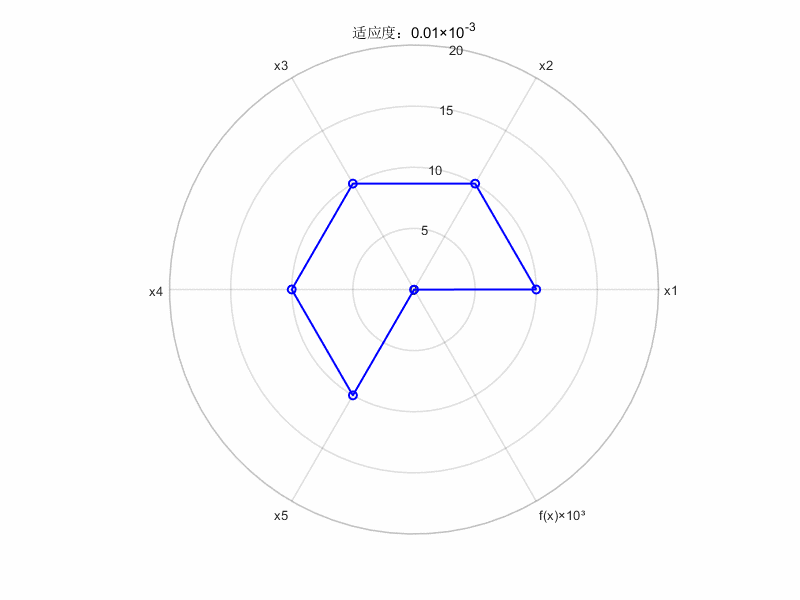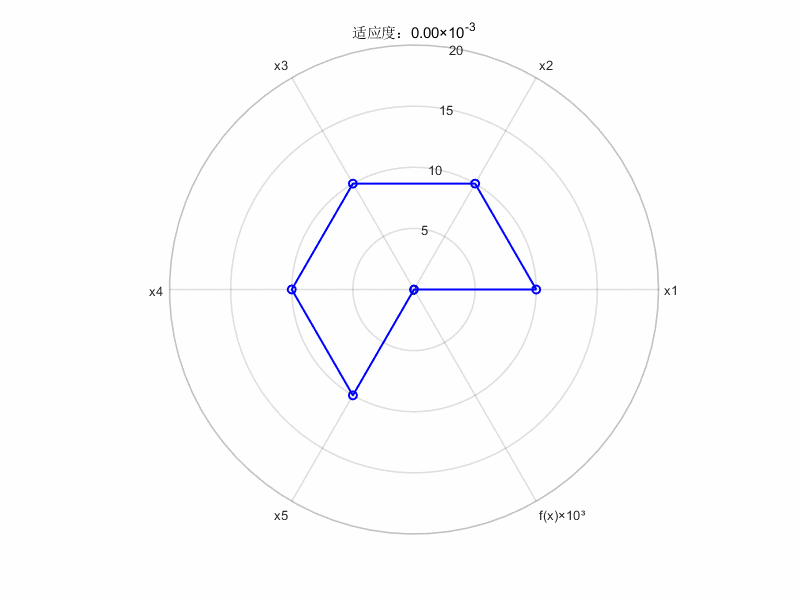
%% =================== 动态雷达图生成 ===================
categories = {'x1', 'x2', 'x3', 'x4', 'x5', 'f(x)×10³'}; % 维度标签
gifName = 'f(x)动态变化雷达图.gif';                        % 输出文件名

% 预处理数据
plotData = [data_global_best_pos, ...
           arrayfun(@(i) objective_func(data_global_best_pos(i,:))*1e3, ...
           (1:size(data_global_best_pos,1)))']; % 添加缩放后的目标函数值

% 创建等角度极坐标
numVars = length(categories);
angles = linspace(0, 2*pi, numVars + 1); 

% 生成动态图
fig = figure('Color','white','Position',[100 100 800 600]);
for k = 1:size(plotData,1)
    % 当前帧数据（闭合处理）
    currentData = [plotData(k,:), plotData(k,1)]; 
    
    % 绘制雷达图
    polarplot(angles, currentData, 'b-o', 'LineWidth', 1.5, 'MarkerSize', 6);
    
    % 图形美化
    title(sprintf('适应度：%.2f×10^{-3}', plotData(k,end)));
    rlim([0 20]);
    thetaticks(rad2deg(angles(1:end-1)));
    thetaticklabels(categories);
    set(gca, 'FontSize', 10, 'LineWidth', 1.2);
    
    % 捕获帧并写入GIF
    frame = getframe(gcf);
    im = frame2im(frame);
    [A, map] = rgb2ind(im, 256);
    if k == 1
        imwrite(A, map, gifName, 'gif', 'LoopCount', Inf, 'DelayTime', 0.5);
    else
        imwrite(A, map, gifName, 'gif', 'WriteMode', 'append', 'DelayTime', 0.5);
    end
end
close(fig);
fprintf('动态图已保存为：%s\n', gifName);