基于FES的远程康复双侧控制

功能性电刺激与基于机器人的远程康复的双侧控制

摘要

目前，远程康复系统通常包括治疗师和患者，治疗师通过言语和视觉交流与患者互动，以评估和监督康复干预。这种机制往往无法提供身体辅助，而身体辅助是物理治疗或职业治疗中的操作方式。在患者端引入一种驱动模式，例如由治疗师远程控制的功能性电刺激（FES）或机器人，以提供治疗或评估和测量康复效果，可以显著改变当前的远程康复技术。本文针对基于功能性电刺激的远程康复，提出了一种位置同步控制器，以实现可远程控制的身体辅助。该新设计的控制器能够在存在恒定双向通信延迟的情况下，实现由FES驱动的人体肢体与远程物理治疗师的机器人操纵器之间的同步。该控制设计克服了一个主要的稳定性分析挑战：由FES驱动的人体肢体中存在的未知且非结构化的非线性肌肉骨骼动力学。为应对这一挑战，通过两个神经网络函数来估计非线性肌肉模型，分别用于逼近非结构化非线性特性，并采用具有在线更新律的自适应控制律处理结构化非线性特性。利用基于李雅普诺夫的稳定性分析证明了系统的全局一致最终有界跟踪性能。通过对健康受试者进行实验验证了状态同步控制器的性能。具体而言，我们展示了对FES诱发的腿部伸展和人工操作的机器人操纵器的双侧控制。实验结果表明，尽管前向和后向通道中存在未知且不同的延迟，该控制器仍能有效实现系统的同步。

1 引言

中风引起的神经功能障碍是美国残疾的首要原因。每年有超过79.5万名个体受到中风影响（Go等2014）。肢体功能丧失会阻碍日常生活活动（ADL），显著限制长期独立性（Mayo等 2002），并增加对美国医疗保健系统的依赖；因此加重美国经济负担。肢体功能的最大恢复通常发生在中风后6个月左右，并从中风后1年开始逐渐下降（Kwakkel等 2003）。为了促进日常生活活动，治疗目标是增强和拉伸肌肉，并重新训练中枢神经系统以自主激活肢体肌肉。康复包括大量由经过培训的治疗师提供的重复性身体锻炼。然而，由于社区数量有限等原因，康复服务提供者、治疗的重复性以及不断上升的劳动力成本，使得中风后6个月幸存者维持和改善肢体功能的能力受到限制。此外，出院后前往诊所的不便通常是获得康复服务的主要障碍。因此，确定中风后提供康复服务最有效且高效的方法至关重要。上述问题以及未来患者数量可能显著增加的情况，促使了物理治疗替代方法的出现。例如，功能性电刺激（FES）、治疗机器人以及称为远程康复的居家康复服务已被提出用于提供治疗性锻炼。

远程康复是指通过电信媒介实现患者与治疗师互动的康复服务应用。目前，远程康复已用于患者评估、咨询、监督和管理（Durfee 等 2007；Zampolini 等 2008）。研究发现，远程康复与标准门诊治疗同样可行，甚至更受参与的治疗师和患者的青睐（Huijgen 等 2008）。Gregory 等（2011）讨论了一项关于远程医疗应用的调查，其中包括物理治疗、职业治疗、言语和语言病理学评估等。已有多个基于视频会议的物理治疗和职业治疗案例被报道，涉及多发性硬化、膝骨关节炎、支气管肺发育不良、中风和帕金森病患者。在所有案例中，均报告了对居住偏远或偏好居家服务的患者有显著改善和益处。Kowalczewski 等（2011）报告了一项关于上肢远程康复的临床研究结果。该研究纳入13名脊髓损伤参与者，用于比较两种基于FES的远程康复治疗方法：（1）传统运动疗法和（2）带有远程监督员的ReJoyce运动疗法。治疗师通过双向语音和视频通信监督受试者。基于互联网的ReJoyce系统相比传统疗法，在手部力量改善方面表现出统计学和临床意义上的显著效果。Hermann 等（2010）研究了通过Ness H200手部康复系统（加利福尼亚州瓦伦西亚Bioness公司）实施的FES程序的疗效。该研究仅涉及一名中风患者与治疗师之间的视频和语音通信。参与者的日常生活活动能力在互联网治疗后有所提高，治疗结束后其患侧上肢功能障碍也有所减轻。一种用于上肢康复的基于网络的远程康复系统，使用力反馈操纵杆和Java治疗软件在Reinkensmeyer 等（2002）中进行了演示。运动数据来自一名慢性中风受试者。研究表明，该系统能够组织治疗程序、吸引用户参与，并追踪因治疗带来的改善。在一项类似但更早的研究中，Rutgers Master II（RM-II）手部手套被用于基于虚拟现实的远程康复系统中的力反馈（Popescu 等 2000）。

Simonsen 等（2014）测试了一种闭环远程康复系统，用于恢复手部功能并记录用户的情绪状态。使用FES辅助手部开合。对FES的反馈由微软Kinect传感器提供。同时，记录并分析中风患者在FES过程中的面部表情以评估其情绪反应。结果显示，Kinect传感器能成功控制手部的开合，但面部表情识别被发现不可靠。

这些远程康复平台缺乏提供外部身体辅助的媒介。为了治疗目的，直到患者的康复达到最大化，在患者端引入一种驱动模式（如功能性电刺激或机器人），以模拟远程诊所中的治疗师，可能是必要的。尽管机器人引导的康复干预是一种可行的选择，但结合功能性电刺激可能具有更大的治疗益处。功能性电刺激是一种通过向运动神经元施加低强度电流来激活骨骼肌的治疗方法。该治疗可通过在皮肤表面应用经皮电极来实施。功能性电刺激之所以有益，是因为它可以增强肌肉力量、防止肌肉萎缩并增加骨密度。此外，功能性电刺激具有神经可塑性效应，因为它有助于重新训练主动运动单位，并重建大脑与运动神经元之间薄弱的连接（Nagai等人 2016；Popovic 等人2012）。目前的康复系统仅简单地拉伸肌肉或使肢体进行活动范围内的运动，只能提供部分所需的治疗，因此可能不如功能性电刺激有效。因此，由于其生理学优势，功能性电刺激在因部分或完全肢体功能丧失而接受远程康复的患者中具有额外的益处（Peckham 和 Knutson 2005）。

在关于远程康复的综述中，Carignan和Krebs （2006）指出，由于通信网络中的带宽有限、数据丢失和传输延迟，双侧机器人远程康复的闭环控制具有挑战性。这些影响会降低物理交互的质量，并可能导致远程会话失稳。在使用功能性电刺激的远程康复系统中，设计一种能够补偿双侧延迟的控制器，因肌肉骨骼动力学的不确定性和高度非线性而变得更加复杂。由于功能性电刺激过程中存在不确定的非线性肌肉行为，近年来许多非线性技术被提出，包括基于神经网络的自适应功能性电刺激控制器已被提出（Sharma 等人2009a，b，2011， 2012；Ajoudani 和 Erfanian 2009；Alibeji 等人 2015；Jezernik 等人 2004；Cheng 等人 2015）。其中一些控制器采用基于李雅普诺夫的稳定性分析设计，通常能够在存在不确定性和非线性的情况下保证控制器稳定性。另一方面，遥操作机器人的双侧控制受到了广泛关注（参见 Chopra 等人 2004，2006，2008a， b及其中参考文献）。然而，很少有研究人员关注为功能性电刺激和机器人设计具有稳定性保证的双边远程康复控制器。在 Kitamura 等人（2015）中，使用了一种基于功能性电刺激的系统来同步主端人体手臂和从端人体手臂，其中采用了一个简单的比例‐积分‐微分 （PID）控制器来调节功能性电刺激。但该方法在存在模型不确定性及时延的情况下未提供任何稳定性保证。在 Alibeji 等人（2014）中，开发了一种具有稳定性保证的基于功能性电刺激的双边遥操作控制器。该控制器实现了由功能性电刺激激活的患者手臂与由治疗师控制的主机器人之间的位置同步。所提出的治疗方法结合了功能性电刺激的优势以及远程康复的便利性。在 Alibeji 等人（2013）中，Sharma（2012）开发的时延补偿控制器被实验性地应用于人体手臂，以抵消与功能性电刺激相关的机电延迟和通信延迟。然而，该控制器并未考虑反馈至主机器人的通信延迟。

为了弥补上述不足，我们提出了一种利用腿部伸展训练机通过功能性电刺激对大腿进行训练的远程康复设置。该功能性电刺激可用于远程与受试者进行交互。这种远程康复设置有望作为一种肌肉增强干预手段，并且由于受试者的改善情况，可进一步应用神经可塑性或其肌肉力量得到改善时，所提出的基于神经网络的框架可以潜在地适应治疗。本文是我们先前研究（Alibeji 等人，2013，2014）的扩展。在本文中，通过修改误差结构进一步优化了控制器，以提高神经网络的有效性，并且最重要的是，该控制器通过在一名健康受试者上的实验得到了验证。此外，我们假设机器人动力学是不确定的，但具有线性可参数化特性，而肌肉骨骼系统的动力学包含结构性和非结构性非线性。因此，针对机器人动力学采用了前馈自适应控制器，而对于肌肉骨骼系统则采用了两个单层前馈神经网络和一个自适应控制律。这两个单层前馈神经网络用于建模非结构性非线性的被动与主动肌肉动力学，自适应控制律则用于处理结构性非线性。状态同步控制器能够在存在通信延迟和环境力的情况下实现全局一致最终有界（GUUB）的状态同步。

2 系统动力学

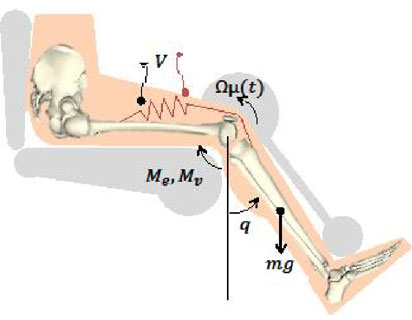
如图1所示，远程康复系统由操作人员控制的机器人操纵器和FES驱动的肌肉骨骼系统组成。n连杆机器人操纵器的动力学方程为
$$
M_r(q_r)\ddot{q} r + C_r(q_r,\dot{q}_r)\dot{q}_r + G_r(q_r) = F_h + \tau_r, \quad (1)
$$
其中 $q_r,\dot{q}_r, \ddot{q}_r \in \mathbb{R}^n$ 分别表示每个关节的角位置、速度和加速度。在(1)中，$M_r \in \mathbb{R}^{n\times n}$ 表示正定惯性矩阵，$C_r \in \mathbb{R}^{n\times n}$ 表示向心/科里奥利矩阵，$G_r \in \mathbb{R}^n$ 表示重力转矩，而 $\tau_r(t) \in \mathbb{R}^n$ 表示电机作用在每个关节上的扭矩。在（1）中，$F_h(t) \in \mathbb{R}^n$ 表示操作人员对机器人施加力所产生的扭矩。为了设计控制器，假设该扭矩由操作人员施加，并建模为一个 PD控制器，其表达式为
$$
F_h(t) = K_p e_d + K_d \dot{e}_d, \quad (2)
$$
其中，$K_p$ 和 $K_d \in \mathbb{R}^+$ 是未知的比例和微分控制增益， $e_d$ 为用户驱动误差，定义为基于操作员意图的期望机器人位置与实际机器人位置之间的差值，$e_d=q_d - q_r$。期望轨迹 $q_d \in \mathbb{R}^n$ 是为机器人和受试者规划的运动，完全由人类操作员控制。为了便于控制设计，可将未知增益 $K_p$ 和 $K_d$ 定义为 $K_p=a_d k_d$ 和 $K_d=a_d$，其中 $a_d$, $k_d \in \mathbb{R}^n$ 为未知常数，且假定其上界分别为 $\bar{a}_d$ 和 $\bar{k}_d \in \mathbb{R}^+$，从而使得 $F_h$ 可表示为
$$
F_h(t) = a_d(\dot{q}_d - \dot{q}_r), \quad (3)
$$
其中 $\dot{q}_d, \dot{q}_r \in \mathbb{R}^n$ 定义为 $\dot{q}_r = \dot{q}_r + k_d q_r$ 和 $\dot{q}_d = \dot{q}_d + k_d q_d$。期望位置和速度是有界的，即 $q_d, \dot{q}_d \in L \infty$：由于 $q_d$ 是一条设计的轨迹，可以证明 $a_d |q_d| \leq \eta$，其中 $\eta \in \mathbb{R}^+$ 是一个常数。

注释1 期望轨迹$q_d$是由操作人员为机器人操纵器和 FES系统规划的运动。因此，治疗师可以根据对患者活动范围的先验知识以及在治疗过程中观察到的情况来定制轨迹。

FES驱动的肌肉骨骼系统动力学表示为：
$$
J(q_s)\ddot{q}_s + C_s(q_s,\dot{q}_s) \dot{q}_s + M_v(\dot{q}_s) + M_e(q_s) + M_g(q_s) + d(t) = C_s(t) - F_e(t); \quad (4)
$$
$$
C_s(t) = F_m f^T(q_s) g(q_s,\dot{q}_s) u(t); \quad (5)
$$
其中，$q_s、\dot{q}_s、\ddot{q}_s \in \mathbb{R}^n$ 分别表示每个关节的角位置、速度和加速度。在(4)中，$J \in \mathbb{R}^{n\times n}$ 表示固定在测试装置中的肢体的未知惯性，$C \in \mathbb{R}^{n\times n}$ 表示向心/科里奥利矩阵，$M_v \in \mathbb{R}^n$ 表示由肌肉的被动弹性特性产生的力矩，$M_e \in \mathbb{R}^n$ 表示由肌肉的被动黏性特性产生的力矩，$M_g \in \mathbb{R}^n$ 表示作用在肢体上的重力扭矩，$d(t) \in \mathbb{R}^n$ 表示系统中可能出现的任何扰动。关于$M_e$、 $M_v$和$M_g$的详细定义，请参见Sharma等（2011）。FES系统的输入$C_s(t) \in \mathbb{R}^n$ 是使用FES产生的扭矩，$F_e (t) \in \mathbb{R}^n$ 是肌肉骨骼系统和环境之间的相互作用力。

在(5)中，$F_m \in \mathbb{R}^n$ 表示肌肉产生的恒定最大等长力，$f \in \mathbb{R}^n$ 表示随关节角度变化的正力臂，而 $g \in \mathbb{R}^{n\times n}$ 表示肌肉力‐长度和力‐速度关系的未知非线性函数。

用于引起肌肉收缩的归一化电压表示为$u \in \mathbb{R}^n$，并采用分段线性函数建模，该函数也称为募集曲线（Schauer 等，2005），即
$$
u(t) = \text{sat}[v(t)] =
\begin{cases}
0 & v < v_{\min} \
\frac{v(t) - v_{\min}}{v_{\max} - v_{\min}} & v_{\min} \leq v \leq v_{\max} \
1 & v > v_{\max}
\end{cases}; \quad (6)
$$
其中 $v_{\min} \in \mathbb{R}^n$ 是肌肉产生张力所需的最小电压，而 $v_{\max} \in \mathbb{R}^n$ 是在未观察到力或运动显著增加时的最小电压，或受试者可耐受的最大电压水平。在（6）中，施加的刺激电压表示为 $v \in \mathbb{R}^n$。为了简化控制结构和推导过程，本模型忽略了肌肉激活动力学。本文探讨了式（4）中的环境相互作用力 $F_e$ 被建模为与位置和速度成正比的被动力，并定义为
$$
F_e(t) = a_s \dot{q}_s + k q_s, \quad (7)
$$
其中$a_s; k \in \mathbb{R}^n$为未知常数，且$a_s$被$\bar{a}_s \in \mathbb{R}^+$所界定。

3 控制设计

控制目标是设计一组控制器，以在存在通信延迟的情况下通过网络实现机器人操纵器与肌肉骨骼系统之间的状态同步。在实际的网络化控制系统中，由于数据包可能经过不同的网络路径，前向和反向路径中的时间延迟通常不同（Li 等人 2015）。因此，位置误差定义为
$$
e_r(t) = q_s(t - \tau_{sr}) - q_r(t), \quad e_s(t) = q_r(t - \tau_{rs}) - q_s(t);
$$
其中 $\tau_{sr}, \tau_{rs} \in \mathbb{R}^+$ 分别是机器人操作臂端和肌肉骨骼系统端通信网络中的未知延迟。为了便于进行稳定性分析，定义以下辅助误差为
$$
r_r = \dot{e}_r + k_r e_r, \quad r_s = \dot{e}_s + k_s e_s;
$$
其中 $k_r、k_s \in \mathbb{R}^+$ 为控制增益。机器人操纵器将采用自适应控制算法来估计机器人的未知参数。肌肉骨骼系统将采用基于神经网络的自适应非线性控制算法，以估计非线性和不确定的肌肉动态特性。

符号说明/假设

为了简化控制设计，采用以下符号和假设：
时间函数表示法被省略（例如，$e(t) \to e$），任何延迟项均用下标表示（例如，$e(t - \tau_d) \to e_{\tau_d}$）。
矩阵的弗罗贝尼乌斯范数表示为 $|\cdot|_F$。
函数 $X(q_s, \dot{q}_s) \in \mathbb{R}^{n\times n}$ 被引入并定义为 $X = F_m f^T g$，其中 $F_m$、$f$ 和 $g$ 在公式 (5) 中已给出。此外，假设 $|X|_F \in \mathbb{R}^+$，以确保对第二个神经网络的有界性进行合理约束。该假设是合理的，因为肌肉具有特定的物理特性。当肌肉处于完全伸长状态时，肌肉张力才会降至零；而在完全缩短时，肌肉张力显著降低但不为零（Winter 2009）。肢体的活动范围可确保肌肉永远不会完全伸长，因此力‐长度关系不会降至零。力‐速度关系由一个非零数界定，因为它仅在肌肉缩短速度接近其最大值时才等于零，而该最大值超出了本控制问题中施加的速度范围。需要注意的是，与我们早期的研究（Sharma 等，2011，2009）不同，此处并未假设也不要求 $X$ 的一阶时间导数是有界的。
假设机器人与肌肉骨骼动力学的结构化非线性是线性可参数化的（例如，$Yh = M\dot{q} + C\dot{q} - G$），其中 $h \in \mathbb{R}^p$ 是包含 $p$个未知参数的向量，$Y \in \mathbb{R}^{n\times p}$ 是回归矩阵。
肌肉骨骼动力学中的干扰项$d(t)$由常数界定，使得 $|d| \leq \bar{d}$，其中$\bar{d} \in \mathbb{R}^+$是一个常数。

3.1 闭环机器人系统

机器人操纵器的闭环误差系统通过将$r_r$的时间导数与 $M_r$相乘而得到
$$
M_r \dot{r} r = M_r \ddot{e}_r + k_r M_r \dot{e}_r:
$$
代入（1）中的机器人动力学并加上和减去$C_r r_r$后，结果变为
$$
M_r \dot{r}_r + C_r r_r = Y_r h_r - a_d \dot{q}_d - \tau_r; \quad (8)
$$
其中动力学中的线性可参数化项被分组为 $Y_r h_r$
$$
Y_r h_r = M_r \ddot{q} {s\tau_{sr}} + a_d \dot{q}_r + C_r (\dot{q}_r + r_r) + G_r + k_r M_r \dot{e}_r:
$$
机器人操纵器的控制输入定义为
$$
\tau_r(t) = \hat{\tau}_r(t) + Y_r \hat{h}_r; \quad (9)
$$
其中$Y_r \hat{h}_r$是线性可参数化机器人动力学$Y_r h_r$的估计值， $\hat{\tau}_r(t)$是机器人的协调扭矩，其定义为
$$
\hat{\tau}_r = k_r r_r; \quad (10)
$$
其中 $k_r \in \mathbb{R}^+$为控制增益。尽管通信延迟未知，将(9)代入(8)可得
$$
M_r \dot{r}_r + C_r r_r = Y_r \tilde{h}_r - a_d \dot{q}_d - \hat{\tau}_r; \quad (11)
$$
其中 $\tilde{h}_r = h_r - \hat{h}_r$ 定义为参数估计误差。用于修改参数估计向量的更新律定义为
$$
\dot{\hat{h}}_r = \text{proj}(\Gamma_1 Y_r^T r_r); \quad (12)
$$
其中 $\Gamma_1 \in \mathbb{R}^{p\times p}$ 表示一个正定增益矩阵。

3.2 闭环肌肉骨骼系统

通过将$r_s$的时间导数乘以$J$，利用(4)，并在方程两边同时加上项$C_s r_s$，建立肌肉骨骼动力学的闭环系统，结果为
$$
J \dot{r} s + C_s r_s = J \ddot{q} {r\tau_{rs}} + C_s(\dot{q} s + r_s) + M_v + M_e + M_g + d - X u + F_e + k_s J \dot{e}_s; \quad (13)
$$
式(13)中的未知非线性项被归入辅助函数$f(q_s,\dot{q}_s)$以及线性参数化项$Y_s h_s$，定义为
$$
f = M_v + M_e + M_g + C_s \dot{q}_s + a_s \dot{q}_s + k q_s; \quad (14)
$$
$$
Y_s h_s = J \ddot{q} {r\tau_{rs}} + k_s J \dot{e} s + C_s r_s; \quad (15)
$$
表达式（13）可以写成
$$
J \dot{r}_s + C_s r_s = f + Y_s h_s - X u + d; \quad (16)
$$
控制律设计为
$$
u = W^{-1} (\hat{u} + \hat{f} + Y_s \hat{h}_s); \quad (17)
$$
其中$Y_s \hat{h}_s$是$Y_s h_s$中线性可参数化项的估计值，$W$定义为
$$
W = \hat{X} + (\rho(\hat{X}) + b) I {n\times n}; \quad (18)
$$
为避免当$X$等于零时出现奇异性，将$\hat{X}$的谱半径、$\rho(\hat{X}) \in \mathbb{R}^+$以及控制增益$b \in \mathbb{R}^+$加入到$W$中（Chen 等， 2010年）。基于反馈的附加输入 $\hat{u} \in \mathbb{R}^n$定义如下：
$$
\hat{u} = k_s r_s; \quad (19)
$$
其中 $k_s \in \mathbb{R}^+$ 是一个控制增益。

在（17）和（18）中，$\hat{f} \in \mathbb{R}^n$ 和 $\hat{X} \in \mathbb{R}^{n\times n}$ 表示对辅助函数 $f$ 和肌肉动态函数 $X$ 的近似，它们由两个单层神经网络表示为
$$
f = W^T \rho(y) + \epsilon_1(y); \quad (20)
$$
$$
X = R^T \phi(y) + \epsilon_2(y): \quad (21)
$$
神经网络的输入是增广输入向量 $y \in \mathbb{R}^{2n+1}$，定义为 $y = [1, q_s, \dot{q}_s]^T$。两个神经网络的理想权重矩阵分别表示为 $W \in \mathbb{R}^{N_f \times n}$ 和 $R \in \mathbb{R}^{N_X \times n}$。输入层由 $2n + 1$ 个神经元组成，$N_f$ 和 $N_X$ 分别是两个神经网络隐藏层中的神经元数量，$n$ 是输出层的神经元数量。第一个神经网络从输入层到隐藏层的激活函数表示为 $\rho: \mathbb{R}^{2n+1} \to \mathbb{R}^{N_f}$。第二个神经网络从输入层到输出层的激活函数表示为 $\phi: \mathbb{R}^{2n+1} \to \mathbb{R}^{N_X \times n}$。两个神经网络的未知函数重构误差分别表示为 $\epsilon_1 \in \mathbb{R}^n$ 和 $\epsilon_2 \in \mathbb{R}^{n\times n}$，且是有界的，即 $|\epsilon_1| \leq \bar{\epsilon}_1$ 和 $|\epsilon_2| \leq \bar{\epsilon}_2$，其中 $\bar{\epsilon}_1、\bar{\epsilon}_2 \in \mathbb{R}^+$。用于逼近 $f$ 和 $X$ 的理想神经网络的估计值表示为
$$
\hat{f} = \hat{W}^T \rho(y); \quad (22)
$$
$$
\hat{X} = \hat{R}^T \phi(y); \quad (23)
$$
其中 $\hat{W} \in \mathbb{R}^{N_f \times n}$和$\hat{R} \in \mathbb{R}^{N_X \times n}$是理想权重的估计值。

在(16)式中加入并减去 $W v$，并利用(17)式可得
$$
J \dot{r} s + C_s r_s = \tilde{f} + Y_s \tilde{h}_s - \tilde{X} u + d - \hat{u};
$$
其中函数估计误差定义为 $\tilde{f} = \hat{f} - f$和$\tilde{X} = \hat{X} - W$，且 $\tilde{h}_s = h_s - \hat{h}_s$为参数估计误差。利用部分神经网络性质（Lewis 等人 2003），函数估计误差 $\tilde{f}$ 和 $\tilde{X}$ 可表示为
$$
\tilde{f} = \tilde{W}^T \rho + \epsilon_1, \quad \tilde{X} = \tilde{R}^T \phi + \beta;
$$
其中，神经网络的网络扰动为 $\epsilon_1$和$\beta = \epsilon_2 - (\rho(\hat{X}) + b)I {n\times n}$，且$\beta$是有界的，即满足$|\beta|_F \leq \bar{\beta}$（即$\bar{\beta} \in \mathbb{R}^+$）。权重估计误差定义为 $\tilde{W} = W - \hat{W}$和$\tilde{R} = R - \hat{R}$。根据后续的稳定性分析，用于调整各层权重的更新律定义为
$$
\dot{\hat{h}}_s = \text{proj}(\Gamma_2 Y_s^T r_s);
\dot{\hat{W}} = \text{proj} (\Gamma_3 r r_s^T);
\dot{\hat{R}} = \text{proj} (-\Gamma_4 \phi u r_s^T); \quad (24)
$$
其中$\Gamma_2 \in \mathbb{R}^{g\times g}$, $\Gamma_3 \in \mathbb{R}^{N_f\times N_f}$和$\Gamma_4 \in \mathbb{R}^{N_X\times N_X}$为正定增益矩阵，$g \in \mathbb{R}^+$表示$h_s$中未知参数的个数。更新律采用投影算法$\text{proj}$，以确保权重是有界的（Dixon 等人， 2003）；因此，神经网络的权重满足$|\hat{f}| \leq \omega_1$且$|W^{-1}|_F \leq \omega_2$，其中$\omega_1、\omega_2 \in \mathbb{R}^+$为已知常数。FES系统的最终闭环系统为
$$
J \dot{r}_s = -C_s r_s + \tilde{W}^T \rho + Y_s \tilde{h}_s - \tilde{R}^T \phi + \beta u + \epsilon_1 + d - \hat{u}; \quad (25)
$$

4 稳定性分析

定理1 考虑(1)–(7)中描述的基于功能性电刺激的非线性双边远程康复系统。在存在未知的恒定通信延迟的情况下，若以下增益条件成立，则根据(9)和(17) 定义的控制输入以及(12)和 (24)定义的更新律，系统中的所有信号均为半全局一致有界：
$$
k_r > \frac{1}{2} + \frac{1}{2v_1}, \quad k_s > \frac{1}{2} + \frac{1}{2v_2}, \quad k_r > \frac{1}{2}, \quad k_s > \frac{1}{2}
$$
其中$v_1$和$v_2 \in \mathbb{R}^+$是随后定义的任意常数。

定义一个正定的李雅普诺夫候选函数 $V(x,t) \in \mathbb{R}$
$$
V = \frac{1}{2} r_r^T M_r r_r + \frac{1}{2} r_s^T J r_s + \frac{1}{2} e_r^T e_r + \frac{1}{2} e_s^T e_s + \frac{1}{2} \tilde{h}_r^T \Gamma_1^{-1} \tilde{h}_r + \frac{1}{2} \tilde{h}_s^T \Gamma_2^{-1} \tilde{h}_s + \frac{1}{2} \text{tr}(\tilde{W}^T \Gamma_3^{-1} \tilde{W}) + \frac{1}{2} \text{tr}(\tilde{R}^T \Gamma_4^{-1} \tilde{R}). \quad (26)
$$

由于投影算法（Dixon 等人，2003）被用于将 $\hat{h} r$、$\hat{h}_s$、$\hat{W}$ 和 $\hat{R}$ 限制在一定范围内，李雅普诺夫候选函数可被上下界约束为
$$
k {\min} |x|^2 \leq V \leq k_{\max} |x|^2 + w, \quad (27)
$$
其中 $k_1; k_2; w \in \mathbb{R}^+$ 是已知常数，且 $x \in \mathbb{R}^{4n}$ 定义为
$$
x = [r_r^T, r_s^T, e_r^T, e_s^T]^T. \quad (28)
$$

在使用(11)和(25)后，$V(x, t)$的时间导数可以表示为
$$
\dot{V} = \frac{1}{2} r_r^T M_r \dot{r}_r + r_r^T (-C_r r_r + Y_r \tilde{h}_r - a_d \dot{q}_d - \hat{\tau}_r) + \frac{1}{2} r_s^T J \dot{r}_s + r_s^T (-C_s r_s + \tilde{W}^T \rho + Y_s \tilde{h}_s - \tilde{R}^T \phi + \beta u + \epsilon_1 + d - \hat{u}) + e_r^T \dot{e}_r + e_s^T \dot{e}_s + \tilde{h}_r^T \Gamma_1^{-1} \dot{\hat{h}}_r + \tilde{h}_s^T \Gamma_2^{-1} \dot{\hat{h}}_s - \text{tr}(\tilde{W}^T \Gamma_3^{-1} \dot{\hat{W}}) - \text{tr}(\tilde{R}^T \Gamma_4^{-1} \dot{\hat{R}}). \quad (29)
$$

将（29）中的神经网络项重新归入 $\text{tr}{\cdot}$ 函数，得到
$$
\dot{V} = \frac{1}{2} r_r^T M_r \dot{r}_r + r_r^T (-C_r r_r + Y_r \tilde{h}_r - a_d \dot{q}_d - \hat{\tau}_r) + \frac{1}{2} r_s^T J \dot{r}_s + r_s^T (-C_s r_s + Y_s \tilde{h}_s - \beta u + \epsilon_1 + d - \hat{u}) + e_r^T \dot{e}_r + e_s^T \dot{e}_s - \tilde{h}_r^T \Gamma_1^{-1} \dot{\hat{h}}_r + \tilde{h}_s^T \Gamma_2^{-1} \dot{\hat{h}}_s - \text{tr}(\tilde{W}^T \Gamma_3^{-1} \dot{\hat{W}} - r r_s^T) - \text{tr}(\tilde{R}^T \Gamma_4^{-1} \dot{\hat{R}} + \phi u r_s^T). \quad (30)
$$

通过使用更新律（24）和（12），消去相似项，并利用斜对称性质 $r_r^T (\dot{M}_r - 2C_r) r_r = 0$ 和 $r_s^T (\dot{J} - 2C_s) r_s = 0$，(30) 可写为
$$
\dot{V} = r_r^T (-a_d \dot{q}_d - \hat{\tau}_r) + r_s^T (-\hat{\tau}_r - \beta u + \epsilon_1 + d - \hat{u}) + e_r^T \dot{e}_r + e_s^T \dot{e}_s.
$$
使用(10)和(19)，我们得到
$$
\dot{V} = r_r^T (-a_d \dot{q}_d - k_r r_r) + r_s^T (-k_s r_s - \beta u + \epsilon_1 + d) + e_r^T (r_r - k_r e_r) + e_s^T (r_s - k_s e_s).
$$
利用(2)、(7)和(17)，可将上述方程重排为
$$
\dot{V} = -k_r r_r^T r_r - k_s r_s^T r_s - k_r e_r^T e_r - k_s e_s^T e_s + e_r^T r_r + e_s^T r_s - a_d r_r^T \dot{q}_d + r_s^T (-\beta u + \epsilon_1 + d). \quad (31)
$$

通过使用以下不等式
$$
|a_d r_r^T \dot{q}_d| \leq \frac{\eta}{k_r} |r_r|, \quad |r_s^T (-\beta u + \epsilon_1 + d)| \leq \frac{\bar{\beta} + \bar{\epsilon}_1 + \bar{d}}{k_s} |r_s|,
|r_r^T e_r| \leq \frac{1}{2} |e_r|^2 + \frac{1}{2} |r_r|^2, \quad |r_s^T e_s| \leq \frac{1}{2} |e_s|^2 + \frac{1}{2} |r_s|^2,
$$
（31）可以被上界约束为
$$
\dot{V} \leq -\left(k_r - \frac{1}{2}\right) r_r^T r_r - \left(k_s - \frac{1}{2}\right) r_s^T r_s - \left(k_r - \frac{1}{2}\right) e_r^T e_r - \left(k_s - \frac{1}{2}\right) e_s^T e_s + \frac{\bar{\beta} + \bar{\epsilon}_1 + \bar{d}}{k_s} |r_s| + \frac{\eta}{k_r} |r_r|. \quad (32)
$$

使用非线性阻尼（Khalil 2002）后，(32) 可进一步上界估计为
$$
\dot{V} \leq -\frac{1}{2} K_{\min} |x|^2 + \frac{\eta^2}{2v_1} + \frac{(\bar{\beta} + \bar{\epsilon} 1 + \bar{d})^2}{2v_2}, \quad (33)
$$
其中 $v_1; v_2 \in \mathbb{R}^+$为常数且
$$
K {\min} = \min\left{k_r - \frac{1}{2} - \frac{1}{2v_1}, k_s - \frac{1}{2} - \frac{1}{2v_2}, k_r - \frac{1}{2}, k_s - \frac{1}{2}\right}.
$$
(33) 可进一步有界化以得到
$$
\dot{V} \leq -\frac{1}{2} K_{\min} |x|^2 + A, \quad (34)
$$
其中 $A = \frac{\eta^2}{2v_1} + \frac{(\bar{\beta} + \bar{\epsilon} 1 + \bar{d})^2}{2v_2}$。结合(27)，可得以下表达式
$$
\dot{V} \leq -\frac{1}{2} \frac{K {\min}}{k_{\max}} V + B, \quad (35)
$$
其中 $B = \frac{1}{2} K_{\min} k_{\max} w + A$。(35) 可积分得到：
$$
V(x; t) \leq V(0)e^{-\frac{1}{2} \frac{K_{\min}}{k_{\max}} t} + B \left(1 - e^{-\frac{1}{2} \frac{K_{\min}}{k_{\max}} t}\right). \quad (36)
$$
由(36)可知，$V(x,t)$ 指数衰减至一个有界值 $B$，该有界值可通过控制增益最小化。由于 $V \in L_\infty$，状态 $r_r; r_s; e_r; e_s \in L_\infty$。进一步分析可表明 $|x|$ 衰减至半径为 $\sqrt{\frac{2B}{k_{\min}}}$ 的球内。根据哈立德（2002）中的定理4.18，可以得出 $x$ 的原点是半全局一致有界的。

5 实验

在获得匹兹堡大学机构审查委员会批准后，对一名健康受试者（男性，年龄：21岁）进行了实验。实验模拟了一次远程康复会话，其中治疗师的机器人通过功能性电刺激与受试者的大腿相互作用。所提出的控制器用于同步机器人操纵器与受试者大腿的位置，即使存在未知的通信延迟。测试了三种场景：（1）受试者的自主运动被机器人模仿；即机器人作为从动端并跟踪延迟的腿部角度轨迹，（2）操作人员使用机器人通过功能性电刺激来操控受试者腿部；即腿部作为从动端并跟踪延迟的机器人角度轨迹，以及（3）一项交互实验，其中操作人员可以中止受试者的自主运动。

5.1 实验平台

实验在由下肢模拟器和Phantom Omni机器人（Geomagic 公司，美国）组成的实验平台上进行，其中Phantom Omni机器人作为人类操作员的机械臂。
，该机器加装了光电编码器和阻力带供测试对象使用。Phantom Omni 被用作机器人操纵器，供操作人员进行交互。通信网络和延迟在软件中以虚拟方式实现。)

下肢模拟器经过改装，加装了一个分辨率为每转1024 脉冲的增量式光电编码器（恒翔，中国），用于测量膝关节角度。在下肢模拟器上添加了阻力带以产生被动环境力矩，$F_e$ in(7)。Phantom Omni 机器人具有三个电机驱动的自由度，但仅使用其中一个连杆来操纵腿部，其余两个连杆保持固定。采用RehaStim 8通道刺激器（Hassomed 公司，丹麦）对股四头肌进行刺激。刺激方案为电流调制的双相刺激，频率为35赫兹，脉冲宽度为400μs。一对经皮电极（AxelGaard Manufacturing 公司，美国）放置在股四头肌上：一个靠近膝关节，另一个位于第一个电极远端。使用 QPIDe（Quanser 公司，安大略省，加拿大）数据采集（DAQ）板连接传感器，并以1千赫兹的频率实时运行控制器。控制算法在Simulink（MathWorks 公司，美国）中编写，并通过运行于一台Windows机器（英特尔至强3.10 GHz处理器）上。机器人操纵器和FES系统的控制器均在一个程序中实现，并在机器人与FES之间（前向通道）编码了50 毫秒的人工传输延迟，在FES与机器人之间（后向通道）编码了80毫秒延迟。这些网络延迟的选择是为了模拟治疗师端较高质量的互联网连接和患者端较低质量的互联网连接。

5.2 神经网络的离线训练

所提出的控制器使用神经网络（NNs）来逼近（20）和（21）中的函数。然后，控制器基于当前误差在每个时间步长使用单步学习基础在线调整权重。尽管（17）中的控制器不需要对神经网络进行离线训练，但以冷启动/神经网络的随机初始权重运行控制器可能不切实际。因此，在实验期间，神经网络通过离线预训练来为神经网络权重找到一个合理的起始点，并在（24）中使用在线自适应律。由于神经网络被用于逼近不可测量的函数，因此无法通过基于受试者记录数据的批处理方式进行训练。因此，采用来自Popovic´等人（1999）的具有健全受试者参数的肌肉骨骼模型来生成将由神经网络逼近的项。然后，使用反向传播算法（Lewis等，2003）对神经网络进行离线训练。公式（20）和（21）中的函数依赖于肢体位置和速度；因此，从八个具有不同时间段的正弦运动中生成了一组数据。这确保了神经网络能够针对各种可能的肢体位置和速度进行训练。该调优过程不仅找到了权重$\hat{W}$和$\hat{R}$的初始起点，还确定了激活函数的速率和偏置参数$\rho$和$\phi$。

5.3 实验协议和结果

如前所述，对一名健康受试者进行了三组实验。在第一组实验中，测试对象通过主动伸展腿部充当主控端角色。控制器随后迫使机器人操纵器跟踪其腿部运动。在此设置中，测试对象被指示以三种不同的方式移动腿部：步骤、斜坡和正弦运动。三次试验中延迟的受试者膝关节角度、机器人连杆角度以及机器人的输入和功能性电刺激（FES）绘制于图3中。

在第二组实验中，系统的驱动力来自操作人员，操作人员操纵作为主控端的机器人，而受试者的腿部作为从动端跟踪机器人的延迟轨迹。操作人员试图重复相同的三种运动类型：与第一组实验相同，即步骤、斜坡和正弦运动。三次试验中延迟的机器人连杆角度、受试者膝关节角度以及机器人的输入和功能性电刺激信号如图4所示。从图中可以看出存在稳态误差。这是可以预期的，因为系统没有积分控制，且神经网络是基于参数可能与测试对象不匹配的模型进行预训练的。在中间图中可以观察到操作人员接收到触觉反馈的证据，其中电机输入为负值。这意味着控制器实质上意识到受试者正在无法到达操作人员设定的期望位置，并在机器人操纵器上产生负扭矩，操作人员会将其感知为阻力（图4）。

在最后一组实验中，测试了使用功能性电刺激作为触觉反馈的效果。在此实验中，测试对象被要求自主移动腿部，类似于第一组实验中的斜坡试验。操作人员随后观察由机器人操纵器产生的同步运动。在下坡阶段（即腿部弯曲），操作人员限制机器人不能超过某一位置。尽管测试对象试图自主屈膝，其腿部仍会模仿受限制的机器人运动。这种机器人与腿部的协调可以解释如下：控制器检测到机器人操纵器的运动受阻，因此增加电刺激量，导致股四头肌收缩，从而限制测试对象进一步向下运动。该实验的结果如图5所示。图5的上方图表中用箭头标出了操作人员阻碍机器人运动的时刻。从电机输入图中可以观察到操作人员干预的位置；输入变为负值，表示机器人试图朝与操作人员预期方向相反的方向运动。此外，测试对象表示他感觉功能性电刺激更强，有效阻止了当操作人员阻断机器人运动时他的膝盖弯曲。

6 讨论

本文旨在提出一种用于基于功能性电刺激的远程康复系统的双侧控制方案，并通过实验验证其有效性。借助该系统，患者可在家中舒适地接受治疗过程，同时由治疗师进行监督并与之进行物理交互，以维持肌肉力量，并帮助加强大脑与运动神经元之间的神经连接。该方案的优势在于将功能性电刺激（FES）整合到远程康复过程中。针对中风等疾病的患者，治疗过程不仅包括增加关节活动范围和进行肌肉拉伸练习，还需要增强虚弱的肌肉。仅能拉伸或带动关节活动的系统只能提供部分所需的治疗。因此，由于其生理优势，在针对肢体功能部分或完全丧失患者的远程康复中，功能性电刺激是一种有益的补充（Peckham 和 Knutson 2005）。此外，功能性电刺激具有神经可塑性效应，有助于重新训练主动运动单位，并重建大脑与运动神经元之间薄弱的神经连接（Nagai等人 2016； Popovic 等人 2012）。

所开发的双侧控制方案克服了在实时控制中使用功能性电刺激（FES）带来的一些挑战。尽管存在不确定且高度非线性的肌肉骨骼动力学以及未知的恒定通信延迟，所提出的非线性控制方案已被证明是稳定的。然而，需要注意的是，通信延迟的大小会影响增益调谐，从而影响所达到的性能水平。该控制器的另一个优点是，当患者的肌肉骨骼动力学由于肌肉力量增加或任何神经可塑性效应而发生变化时，神经网络（NN）能够适应肌肉模型的变化。控制器中使用第二个神经网络有助于避免在控制器中需要加速度信息或对 X函数的时间导数进行有界性假设。神经网络的在线适应也有益处，因为已有证据表明，在上运动神经元损伤后，由于痉挛，力‐长度/力‐速度关系会发生变化（Gao 和 Zhang 2008；Gray 等人。2012）。所提出方案的适应性有可能应对由痉挛引起的动力学变化。然而，该控制器在这些情况下的适应能力仍有待验证。

在康复疗程中，患者通常在肢体可活动的活动范围方面存在差异。例如，一位患者的膝关节挛缩可能会严重限制其活动范围。因此，所提出系统的优点之一在于治疗师能够控制患者的关节角度轨迹。这一点极为有益，因为治疗过程可以针对每位患者进行个性化定制，并且可以防止受伤。此外，控制器中的触觉反馈功能（在第三组实验中强调）将为治疗师提供观察依据，使其能够据此调整轨迹。

7 结论

本文提出了一种控制器，可实现基于功能性电刺激的双边远程康复系统在前向和后向通道中存在不匹配未知通信延迟情况下的位置同步。所提出的控制器利用离线预训练的人工神经网络来补偿非结构化非线性肌肉骨骼动力学，并采用基于自适应的控制器处理肌肉骨骼和机器人系统中的结构化非线性动力学。通过李雅普诺夫稳定性分析证明了该控制器具有一致最终有界跟踪性能。该控制器已在一名健康男性受试者上进行了实验验证，展示了其在远程康复设置中的可行性。未来实验将在中风患者身上进行，以验证其临床相关性。