Redis 技术内幕——布隆过滤器

现有 50 亿个电话号码，如何快速准确判断某 10 万个电话号码是否在这 50 亿中。

如果通过数据库查询实现会非常慢。
如果数据预放在集合中，50 亿 x 8 字节，大概需要 40 GB内存，内存浪费或不够。
如果使用 hyperloglog 存储，可以使用很小的内存判断数据是否在 hyperloglog 里，但是结果会不准确。

类似问题还有很多，例如垃圾邮件过滤、文字处理软件（例如 Word）错误单词检测、网络爬虫重复 url 检测、Hbase 行过滤等。

基于这类问题，就引出了布隆过滤器。

布隆过滤器是 1970 年伯顿.布隆提出，用很小的空间，解决上述类似问题。

1.布隆过滤器原理

实现原理：一个很长的二进制向量和若干个哈希函数。

布隆过滤器是一个 bit 向量或者说 bit 数组，长这样：

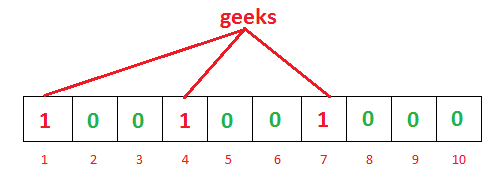
如果我们要映射一个值到布隆过滤器中，我们需要使用多个不同的哈希函数生成多个哈希值，并对每个生成的哈希值指向的 bit 位置 1，例如针对值 “geeks” 和三个不同的哈希函数分别生成了哈希值 1、4、7，则上图转变为：

我们现在再存一个值 “nerd”，如果哈希函数返回 3、4、5 的话，图继续变为：

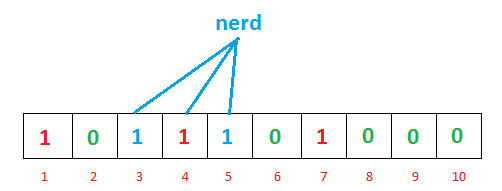
值得注意的是，4 这个 bit 位由于两个值的哈希函数都返回了这个 bit 位，因此它被覆盖了。

m 个二进制向量，n 个预备数据，k 个 hash 函数。构建布隆过滤器：n 个预备数据走一遍上面过程。判断元素是否存在：走一遍上面过程，如果都是 1，则表明存在，反之不存在。

2.布隆过滤器误差率

误差是肯定存在的，跟 m/n 的比率和 hash 函数的个数有关系，m/n 的比率越大，误差越低，hash 函数的个数越多，误差越低。

1 个元素，1 个 hash 函数，任意一个比特为 1 的概率为 $1/m$，依然为 0 的概率为 $1-(1/m)$；
1 个元素，k 个 hash 函数，依然为 0 的概率为 $(1-(1/m){)}^k$；
n 个元素，k 个 hash 函数，依然为 0 的概率为 $(1-(1/m){)}^{nk}$，被设置为 1 的概率为 $1-(1-(1/m){)}^{nk}$；
新元素全中的概率为 (1−(1−(1/m))nk)k(1 - (1- (1/m))^{nk})^{k}(1−(1−(1/m))