leetcode----201. Bitwise AND of Numbers Range

最新推荐文章于 2026-01-05 22:36:07 发布

原创最新推荐文章于 2026-01-05 22:36:07 发布 · 215 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #位运算

leetcode 专栏收录该内容

101 篇文章

订阅专栏

本文探讨了LeetCode上的一道题目，要求计算区间[m,n]内所有数的按位与结果。文章分析了几种特殊情况，并提供了一种低效但直观的解决方案，随后提出了改进算法，显著提高了运行效率。

链接：

https://leetcode.com/problems/bitwise-and-of-numbers-range/

大意：

给定两个数m，n。满足：0 <= m <= n <= Integer.MAX_VALUE。要求求出区间[m,n]所有数依次与运算的结果。例子：

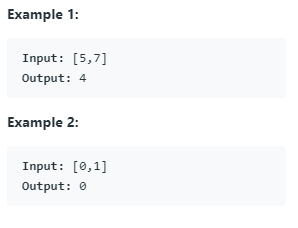
思路：

首先判断几种特殊情况：

m == 0，则可以直接返回m（0）
m == n，也可以直接返回m。因此和上一种情况可以合并
m < n && n = 2 ^ x（即n为2的次方幂），此时可以直接返回0

除了上述的特殊情况外，其余情况就老老实实求吧...（后来发现可以解决，但是效率极低）

代码：

class Solution {
    public int rangeBitwiseAnd(int m, int n) {
        if (m == 0 || m == n)
            return m;
        // m < n && n = 2 ^ x
        if ((n & (n - 1)) == 0)
            return 0;
        // m < n && n != 2 ^ x
        int res = Integer.MAX_VALUE;
        while (m <= n) {
            res = res & m & n;
            if (res == 0)
                return 0;
            m++;
            n--;
        }
        return res;
    }
}

结果：

结论：

时间效率确实低。。。需要改进

改进：

class Solution {
    public int rangeBitwiseAnd(int m, int n) {
        if (m == 0 || m == n)
            return m;
        // m >= 1 并且 n > m(即 n > 1) 若(m,n]中有一个数为2^x，则返回0
        long r = 1; // r为一个2的幂次方数 使用long解决1左移31位溢出的问题
        while ((r << 1) <= n) {
            if ((r << 1) > m)
                return 0;
            r <<= 1;
        }
        // 能走到这 表明[m,n]肯定没有跨区间 如：[5,7] 而[5,9]则为跨区间 既然没跨区间 则对应与运算结果在该位置的二进制数肯定为1
        return (int)r + rangeBitwiseAnd(m - (int)r, n - (int)r);
    }
}