数字图像处理第三章

_Taylor

已于 2023-05-19 19:55:05 修改

阅读量601

点赞数

文章标签： python 计算机视觉人工智能

于 2023-05-15 14:41:00 首次发布

本文链接：https://blog.youkuaiyun.com/sketch_2314/article/details/130558166

版权

本文介绍了图像处理中的灰度变换和空间滤波基础知识，包括图像反转、对数变换、伽马变换和分段线性变换等方法，以及直方图处理的均衡化和规定化。此外，还探讨了空间滤波的基本原理，如图像平滑和锐化，用于消除噪声和增强图像细节。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

灰度变换与空间滤波

1.前言

由之前学习过的章节可以知道，空间图像域是包含图像中的像素的平面，也就是图像平面本身，本章节就针对于图像的空间域进行相关知识和技术原理的笔记总结，参考教材为《数字图像处理》（第四版）冈萨雷斯

2.灰度变换和空间滤波基础

本章的空间域处理基于表达式： $g (x, y) = T [f (x, y)]$ 其中f(x,y)是输入图像，g(x,y)是输出图像，T是定义在点a(x,y)的一个算子（类似于一个函数运算，应用在一幅或一组图像的像素上）。
整个灰度处理过程就是从f中的一个像素点a开始，把T运用到a的领域（以a像素点为中心的外围一圈3x3的像素）上，输出一个值b放到g上对应于f中a的位置上，再处理下一个位置，直到整个图像f处理完。若领域只有1x1的范围，上式中的T就是一个灰度变换函数，即： $s = T (r)$ s与r表示对应g和y中某点的灰度。

以上式为例，灰度变换函数有对比度拉伸函数和阈值处理函数两种：

对比度拉伸：以一个k值为界，小于m的灰度级r，减少s的值，反之亦然。总的就是亮的更亮，暗的更暗
阈值处理：是对比度拉伸的极限形式，小于m的全变成一个灰度级，大的同理

用个简单的图像说明：在这里插入图片描述

3.基本灰度变换函数

主要有四种：
1.图像反转（灰度级数-1-当前灰度，s=L-1-r）
2.对数变换(低灰度较暗的部分变亮)
3.Gamma变换(幂指数校正，可改变对比度，将灰度较窄的区域弄宽)
4.直方图均衡化(增强整体较暗或较亮、对比度不强的图像，使图像变清晰)

1）图像反转

图像反转的主要原理就是根据公式 $s = L - 1 - r$ 得到灰度级在[0,L-1]的反转图像，以下是转换的代码：

from PIL import Image
# 打开图像并转为灰度模式
img = Image.open("./img/test.jpg").convert("L")
# 获取图像的宽度和高度
width, height = img.size
# 遍历每个像素点并反转灰度值
for x in range(width):
    for y in range(height):
        pixel = img.getpixel((x, y))
        img.putpixel((x, y), 255 - pixel)
# 保存反转后的图像
img.save("./img/image_inverted.jpg")

下面是上述代码通过对左图进行灰度反转后的右图结果：

通过灰度反转，能够使暗色区域中的灰色或者白色细节，在医疗等方面有较好的应用。

2）对数变换

对数变换的原理就是根据公式： $s = c l o g (1 + r)$ 对图像进行转换，由对数曲线的形状可以看出是将输入的较窄的灰度值变宽，使灰暗的地方变亮，方便图像的观察，反之亦然。这类变换往往用来扩展图像中的暗像素值，压缩高灰度级值。以下是对数变换的代码：

from PIL import Image
import math
# 打开图像并转换为灰度图像
img = Image.open('./img/test1.tif').convert('L')
# 获取图像的宽度和高度
width, height = img.size
# 对数变换的常数
c = 255 / math.log(1 + img.getextrema()[1])
# 对每个像素应用对数变换
for x in range(width):
    for y in range(height):
        # 获取像素的亮度值
        pixel = img.getpixel((x, y))
        # 计算对数变换后的值
        new_pixel = int(c * math.log(1 + pixel))
        # 更新像素值
        img.putpixel((x, y), new_pixel)
# 保存变换后的图像
img.save('output.jpg')

以下是测试图片的原始和结果图：

大多数的傅立叶频谱都是通过类似的方式进行图像的缩放

3）幂律（伽马）变换

伽马变换的公式为： $s=cr^\gamma$ 和对数变换类似，伽马变换的原理也是将较窄的暗灰度值变宽，反之同理，不过变换的效果是由指数gamma的值决定的，且gamma>1和<1时生成的曲线效果正好相反。下图是当c=1时改变gamma值显示的图形：在这里插入图片描述

伽马校正或伽马编码就是用于校正幂律响应现象的处理过程，有时较大的gamma值会使处理后的图像好于原图，下面是gamma变换的代码：

def gamma_correction(image, gamma):
    """Gamma变换"""
    # 构建Gamma查找表
    inv_gamma = 1.0 / gamma
    table = np.array([((i / 255.0) ** inv_gamma) * 255 for i in range(256)]).astype('uint8')
    # 应用Gamma变换
    return Image.fromarray(cv2.LUT(np.array(image), table))

# 加载图像
img = Image.open("./img/gamma.jpg").convert('L')

# 进行Gamma变换
gamma = 1.5
img_gamma = gamma_correction(img, gamma)

# 显示原图和Gamma变换后的图像
# img.show()
# img_gamma.show()
img.save('gammaput.jpg')

代码的实现如下，从左到右自上而下分别为原图和gamma值为1.5、3.5和6.5的转换图:

感觉和对数变换的区别不大

4）分段线性变换

这个与之前的三种方法互补，优点是形式可以随意复杂，但是需要用户输入很多参数，主要有对比度拉伸、灰度级分层、比特平面分层

对比度拉伸：光照、传感动态范围等都可能产生低对比度图像，该变换可以扩展图像灰度级范围，达到理想的灰度范围，就是通过这个变换可以是对比度变高，对比拉伸代码如下：

from PIL import Image
import numpy as np
def contrast_stretch(img_path, min_percentile=1, max_percentile=99):
    # 打开图像
    img = Image.open(img_path)
    # 转换为灰度图像
    gray_img = img.convert('L')
    # 转换为NumPy数组
    img_array = np.array(gray_img)
    # 计算像素值的最小值和最大值
    min_value, max_value = np.percentile(img_array, (min_percentile, max_percentile))
    # 对图像进行对比度拉升
    img_array = (img_array - min_value) * 255 / (max_value - min_value)
    # 将图像像素值限制在0到255之间
    img_array = np.clip(img_array, 0, 255).astype(np.uint8)
    # 将NumPy数组转换为PIL图像
    result_img = Image.fromarray(img_array)
    return result_img

result_img = contrast_stretch('./img/对比.png', min_percentile=5, max_percentile=95)
result_img.save('./img/duibi.jpg')

效果如下图所示（左图为花粉的低对比度图像，右图为对比度拉伸后的结果）：

可以看出来，对比拉伸的效果还是蛮好的，灰蒙蒙的部分变得清楚多了

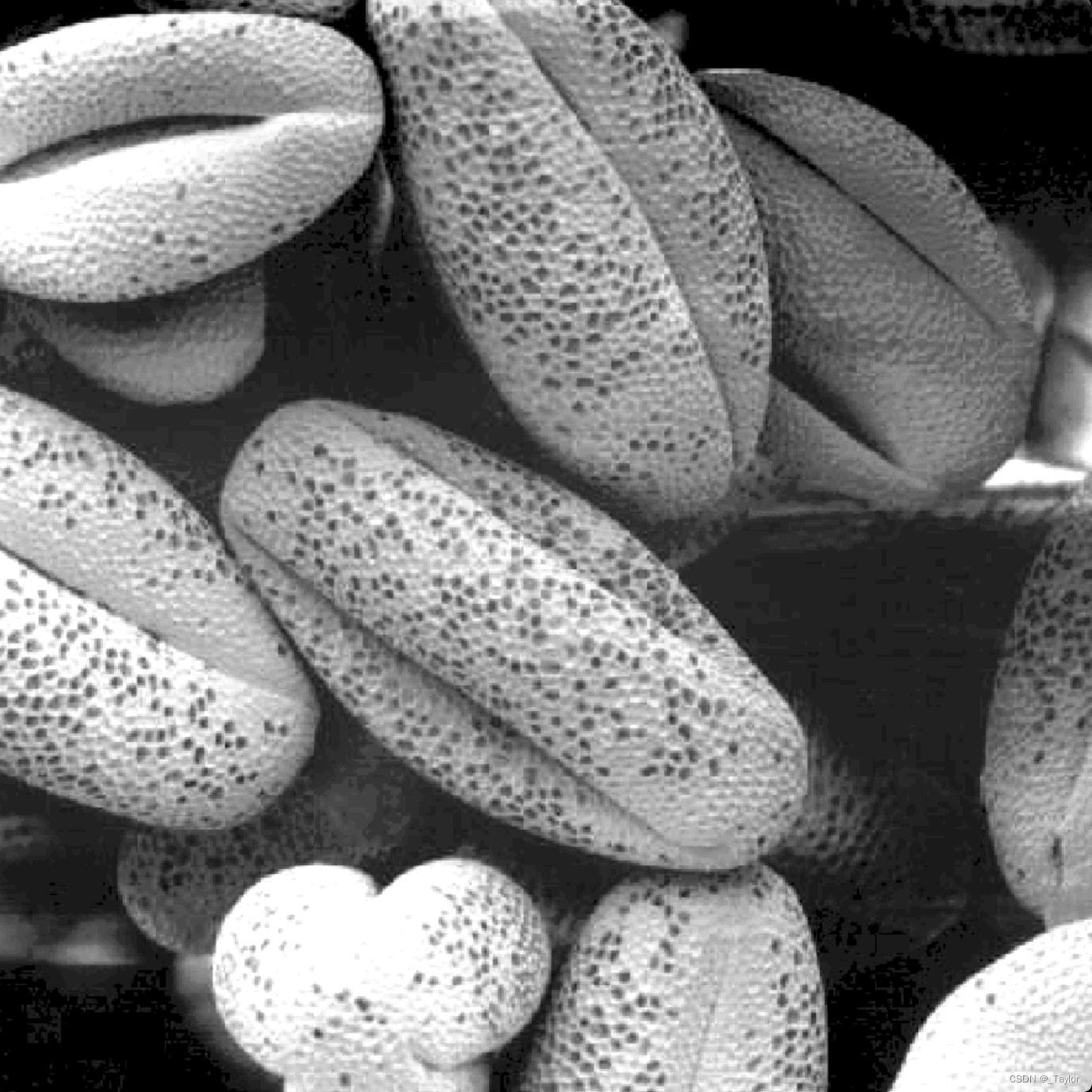灰度级分层：这种方法目的是为了突出图像中的特定灰度区间，它可以由基本的两种方法实现：一种是将给定范围内的灰度值都显示为一个值（也就是一个色），其他的显示为另一个值；另一种是是期望的灰度范围变亮（或变暗），保持其他灰度级不变
比特平面分层：像素值是由比特组成的整数，比特平面分层就是可以涂出特定比特的部分像素，使图像有多分层的灰度值，这样能更好的适应多类型的实际应用

由于分段线性变换的函数比较有共同点，后两个就不放代码和图了

注意⚠️之后部分内容是自己看视频学习的，与书的排版不一致

4.直方图处理：

令r_k，k=0,1,2…,L-1表示一幅L级的f(x,y)的灰度。f的非归一化直方图定义为 $h(r_k)=n_k，k=0,1,2....L-1$ 式中，n_k是f中灰度为r_k的像素的数量，细分的灰度级数称为直方图容器，同理，归一化的直方图定义为 $p(r_k)=\frac{h(r_k)}{MN}=\frac{n_k}{MN}$ 式中M和N分别表示图像的行数和列数，大部分情况都是归一化的直方图，简称直方图或者图像直方图。

目的：使图像变清晰，灰度值变大，值变均匀，算熵先算出每个灰度级像素块的概率，再用求熵的公式。

1）直方图处理均衡化

非线性拉伸，扩展灰度多的像素，缩减灰度少的，使直方图均匀化。过程是求出不同灰度级的概率Pk,累计直方图Sk,最后用公式求出新的概率，具体例子如下（其中L为0-7，即L=8）：在这里插入图片描述

2）直方图处理规定化

将求出的直方图p1与给定的直方图p2进行对比，将两个直方图进行对比，最接近的p1变成p2，具体的例子如下，序号3中的灰度级1与序号5中的灰度级3最接近，则将0映射到3，如序号7中所示，没有转移的灰度级概率就是0：
在这里插入图片描述

3）局部直方图处理

当想增强图像中的几个小区域细节时，就需要局部的像素灰度分布变换，过程是先定义一个领域，将其中心垂直或者水平移动，每次都计算中心点的直方图，得到均衡化或者规定化函数，以此得到中心的灰度值

5.空间滤波基础

原理

即图像f和滤波器核w之间的乘积之和运算

图像增强

目的：消除噪声或模糊图像
噪声分类：
1.椒盐噪声：由图像传感器、传输信号、解码处理等产生黑白相间的亮暗噪声幅值相同，黑白值可以看成极大值和极小值的噪声，出现点随机，用中值滤波效果较好，不是加性或者乘性噪声
2.高斯噪声：图像上每一点都存在噪声，噪声位置随机分布，用均值滤波好（卷积），是加性噪声
增强方法：图像平滑（模糊）和图像锐化（突出过渡部分，寻找边界，增强图像）：
图像平滑有
1.邻均平均滤波（线性）：能够除去突变的像素点，简单但会使图像变模糊。特点是对椒盐噪声平滑效果不好。其步骤是先进行领域平均（卷积）算出中间像素块值，再用中间量进行阈值法平均滤波进行灰度矩阵的修改。这两个晦涩难懂了解一下就明白。
2.中值滤波法（非线性）：将向元灰度值升序排序，中位数作为当前向元输出。特点是对椒盐噪声平滑效果好，但是对于点，线，尖角细节多的不适合。
3.高斯滤波法（线性）：原理与均值滤波器类似，但是算法不同，将各个位置的坐标带入到高斯函数中，得到模版的系数，再用系数求出新的值。其中高斯核的标准差σ看使用的场景，σ小，生成的模版中心系数较大，周围系数较小，平滑效果不是很明显（趋向于中值滤波），反之效果明显（趋向于平均滤波）。

平滑滤波器的代码和图像例子如下，左边是原图，右边是经过平滑滤波器后的图：

import numpy as np
import cv2

def apply_mean_filter(image, kernel_size):
    # 获取图像的宽度和高度
    height, width = image.shape[:2]

    # 创建一个与输入图像相同大小的空白图像
    smoothed_image = np.zeros_like(image, dtype=np.float32)

    # 计算滑动窗口的半径
    radius = kernel_size // 2

    for i in range(height):
        for j in range(width):
            # 计算当前像素周围窗口的边界
            top = max(i - radius, 0)
            bottom = min(i + radius + 1, height)
            left = max(j - radius, 0)
            right = min(j + radius + 1, width)

            # 提取窗口内的像素值
            window = image[top:bottom, left:right]

            # 计算窗口内像素的均值
            mean_value = np.mean(window)

            # 在平滑图像中设置当前像素的值
            smoothed_image[i, j] = mean_value

    # 将浮点图像转换为8位灰度图像
    smoothed_image = np.uint8(smoothed_image)

    return smoothed_image

# 读取图像
image = cv2.imread('./img/pinghua.jpeg', cv2.IMREAD_GRAYSCALE)

# 应用均值滤波器
smoothed_image = apply_mean_filter(image, kernel_size=5)

# 显示原始图像和平滑图像
cv2.imshow('Original Image', image)
cv2.imshow('Smoothed Image', smoothed_image)
cv2.waitKey(0)
cv2.destroyAllWindows()

图像锐化有
1.Prewitt算子（一阶微分算子）：作用是用不同方向的算子检测不同类型的边缘或线，原理是通过一阶微分算子准确定位到边缘线
在这里插入图片描述
2.Sobel算子（一阶微分算子）：作用同Prewitt算子，原理是通过中心点达到平滑的目的，即比Prewitt多了平滑功能

3.拉普拉斯算子（二阶微分算子）：作用是可以检测到灰度突变的点，原理是通过二阶微分算子准确定位到突变的点7 在这里插入图片描述
在有了锐化结果后，在原图上加上或者减去锐化结果，就得到了增强的图像，注意分清是减还是加，防止叠加后的结果变成负值。

锐化滤波器的代码和图像例子如下，左边是原图，右边是经过平滑滤波器后的图：

import numpy as np
import cv2

def apply_sharpen_filter(image):
    # 定义锐化卷积核
    kernel = np.array([[0, -1, 0],
                       [-1, 6, -1],
                       [0, -1, 0]])

    # 对图像进行卷积操作
    sharpened_image = cv2.filter2D(image, -1, kernel)

    return sharpened_image

# 读取图像
image = cv2.imread('./img/ruihua.jpeg', cv2.IMREAD_GRAYSCALE)

# 应用锐化滤波器
sharpened_image = apply_sharpen_filter(image)

# 显示原始图像和锐化后的图像
cv2.imshow('Original Image', image)
cv2.imshow('Sharpened Image', sharpened_image)
cv2.waitKey(0)
cv2.destroyAllWindows()