泊松分布
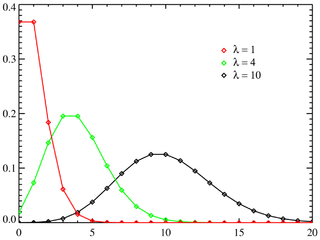
假设概率分布是一致的,例如不会因时间段不同而异,又假设各事件的概率是不相关的(即不相互影响),符合泊松分布Poission distribution。例如某个路口一小时内有多少量车经过。
E(X)=λ,期望值是λ。我们将计算P(X=k)时出现的概率。
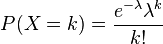
如果根据二项分布进行计算,每一分钟有一辆车经过则为状态成功,没有则为另一状态,每分钟的期望值是λ/60。但这样计算有一个问题,如果一分钟内同时有两辆车经过呢?这种计算就不对。如果我们改为一秒钟有一辆车经过为状态成功,没有则为另一个状态,每秒钟的期望值是λ/3600,这样计算会更为精确,因为一秒钟内同时有两辆车的几率会很少,也就是对结果的干扰更少。如果需要更精确,我们将时间分割得更小,也就是λ/n,n趋于无穷,将可推导出泊松





 本文介绍了泊松分布的概念,强调其适用于描述单位时间内随机事件发生的次数,尤其在事件概率一致且互不影响的情况下。通过与二项分布的对比,解释了泊松分布的优势。此外,还探讨了大数定律,说明随着试验次数趋于无穷,事件的平均发生次数将趋近于期望值。文章以投掷硬币为例,阐述了大数定律的直观含义,并鼓励读者学习人工智能。
本文介绍了泊松分布的概念,强调其适用于描述单位时间内随机事件发生的次数,尤其在事件概率一致且互不影响的情况下。通过与二项分布的对比,解释了泊松分布的优势。此外,还探讨了大数定律,说明随着试验次数趋于无穷,事件的平均发生次数将趋近于期望值。文章以投掷硬币为例,阐述了大数定律的直观含义,并鼓励读者学习人工智能。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 9257
9257

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








