Java&C++题解与拓展——leetcode473.火柴拼正方形【模拟退火】

AnjaVon

于 2022-06-02 10:51:04 发布

阅读量374

点赞数 1

分类专栏： leetcode 文章标签： java c++ leetcode 算法

本文链接：https://blog.youkuaiyun.com/sinat_41135487/article/details/125092353

版权

leetcode 专栏收录该内容

96 篇文章

订阅专栏

每日一题做题记录，参考官方和三叶的题解

题目要求

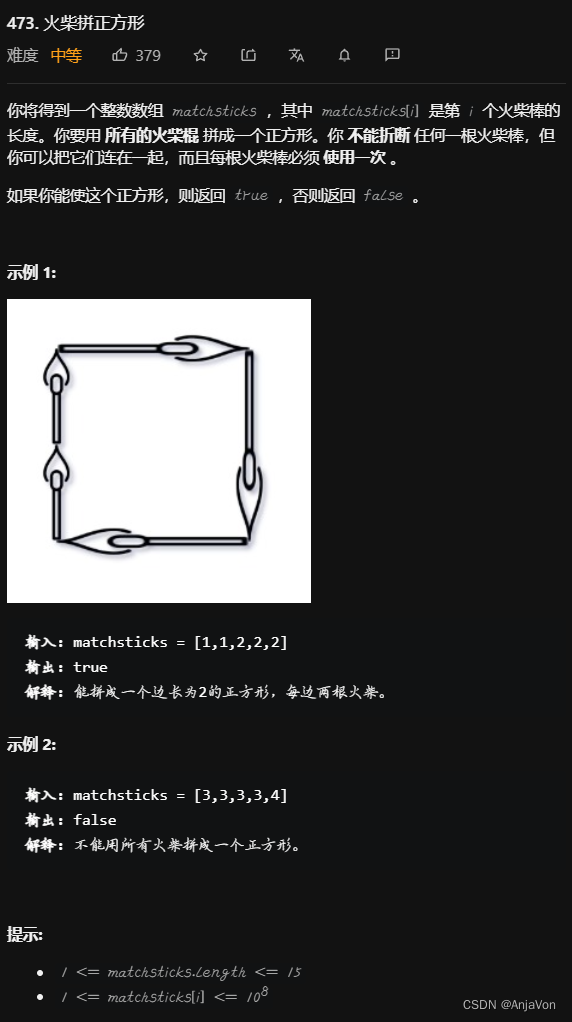
在这里插入图片描述

思路一：DFS

枚举尝试每一种可能性；
剪枝：
- 从大到小搜，避免小的来回放重复搜索；
- 两边长相等则可少搜一种。

Java

class Solution {
    int[] ms;
    int single; // 目标边长
    public boolean makesquare(int[] matchsticks) {
        ms = matchsticks;
        int sum = 0;
        for(int m : ms)
            sum += m;
        if(sum % 4 != 0)
            return false;
        single = sum / 4;
        Arrays.sort(ms);
        return dfs(ms.length - 1, new int[4]); // 倒序搜索
    }
    boolean dfs(int idx, int[] cur) { // cur为当前四条边的边长
        if(idx == -1)
            return true;
        for(int i = 0; i < 4; i++) {
            for(int j = 0; j < i; j++)
                if(cur[j] == cur[i]) // 放在这两条边等价
                    break;
            int u = ms[idx];
            if(cur[i] + u > single) // 超了
                continue;
            cur[i] += u; // 放边i
            if(dfs(idx - 1, cur)) // 放下一根
                return true;
            cur[i] -= u; // 放边i不行
        }
        return false;
    }
}

时间复杂度： $O(4^n)$
空间复杂度： $O(\log n)$ ，排序所需，忽略递归的栈空间

C++

class Solution {
    vector<int> ms;
    int single; // 目标边长
    int cur[4];
public:
    bool makesquare(vector<int>& matchsticks) {
        ms = matchsticks;
        int sum = 0;
        for(int m : ms)
            sum += m;
        if(sum % 4 != 0)
            return false;
        single = sum / 4;
        sort(ms.begin(), ms.end());
        return dfs(ms.size() - 1); // 倒序搜索
    }

    bool dfs(int idx) { // cur为当前四条边的边长
        if(idx == -1)
            return true;
        for(int i = 0; i < 4; i++) {
            for(int j = 0; j < i; j++)
                if(cur[j] == cur[i]) // 放在这两条边等价
                    break;
            int u = ms[idx];
            if(cur[i] + u > single) // 超了
                continue;
            cur[i] += u; // 放边i
            if(dfs(idx - 1)) // 放下一根
                return true;
            cur[i] -= u; // 放边i不行
        }
        return false;
    }
};

时间复杂度： $O(4^n)$
空间复杂度： $O(\log n)$ ，排序所需，忽略递归的栈空间

思路二：模拟退火

用 $n$ 个火柴构造目标边长；
单次迭代流程：
1. 随机选择两个下标，计算「交换下标元素前对应序列的得分」&「交换下标元素后对应序列的得分」
2. 如果温度下降（交换后的序列更优），进入下一次迭代
3. 如果温度上升（交换前的序列更优），以「一定的概率」恢复现场（再交换回来）

另外样例中有一个卡SA的：

这个数据点优秀在于起始排序可以导致我们固定的 calc 逻辑最终落入局部最优。针对这种情况，也很好解决，只需要在执行 SA 之前，先对原数组进行一次随机化打乱即可。

Java

class Solution {
    int[] ms;
    int single, n;
    Random random = new Random(20220601);
    boolean res = false;
    double high = 1e4, low = 1e-4, fa = 0.98;
    int N = 400;

    public boolean makesquare(int[] matchsticks) {
        ms = matchsticks;
        n = ms.length;
        int sum = 0;
        for(int m : ms)
            sum += m;
        if(sum % 4 != 0)
            return false;
        single = sum / 4;
        for(int i = n; i > 0; i--) { // 随机打乱
            int idx = random.nextInt(i);
            swap(idx, i - 1);
        }
        while(N-- > 0)
            sa();
        return res;
    }

    int calc() {
        int diff = 0;
        for(int i = 0, j = 0; i < 4; i++) {
            int cnt = 0;
            while(j < n && cnt < single)
                cnt += ms[j++];
            diff += Math.abs(cnt - single);
        }
        if(diff == 0)
            res = true;
        return diff;
    }
    void sa() {
        for(double t = high; t > low && !res; t *= fa) {
            int a = random.nextInt(n), b = random.nextInt(n);
            int prev = calc();
            swap(a, b);
            int cur = calc();
            int diff = prev - cur;
            if(Math.log(diff / single) > random.nextDouble())
                swap(a, b);
        }
    }

    void swap(int i, int j) {
        int tmp = ms[i];
        ms[i] = ms[j];
        ms[j] = tmp;
    }
}

C++【TLE】

【回头好好学习一下随机数和退火，改改参数康康能不能解决】

class Solution {
    vector<int> ms;
    int single, n;
    bool res = false;
    double high = 1e4, low = 1e-4, fa = 0.98;
    int N = 400;
    

public:
    bool makesquare(vector<int>& matchsticks) {
        ms = matchsticks;
        n = ms.size();
        int sum = 0;
        for(int m : ms)
            sum += m;
        if(sum % 4 != 0)
            return false;
        single = sum / 4;
        for(int i = n; i > 0; i--) { // 随机打乱
            int idx = rand() % i;
            swap(idx, i - 1);
        }
        while(N-- > 0)
            sa();
        return res;
    }

    int calc() {
        int diff = 0;
        for(int i = 0, j = 0; i < 4; i++) {
            int cnt = 0;
            while(j < n && cnt < single)
                cnt += ms[j++];
            diff += abs(cnt - single);
        }
        if(diff == 0)
            res = true;
        return diff;
    }
    void sa() {
        for(double t = high; t > low && !res; t *= fa) {
            int a = rand() % n, b = rand() % n;
            int prev = calc();
            swap(a, b);
            int cur = calc();
            int diff = prev - cur;
            if(log(diff / single) > rand())
                swap(a, b);
        }
    }

    void swap(int i, int j) {
        int tmp = ms[i];
        ms[i] = ms[j];
        ms[j] = tmp;
    }
};