matlab计算差分方程近似值

1.题目

计算3个差分方程的前10个数值近似值，并引入初始误差。并构造表和图的输出。

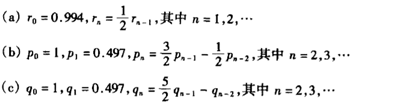
定义10个数，xn为初始误差，根据差分方程，定义rn/pn/qn的值进行计算，最终返回xn-rn/xn-pn/xn-qn的值，以表格/图片输出。

2.代码

（1）rn与xn-rn计算值

n=0:10;

xn=1./(2.^n)

 

r0=0.994;r(1)=r0/2;

for n=2:10

    r(n)=r(n-1)/2

end

rn=[r0,r];

m=xn-rn;

xn-rn生成图片

r0=0.994;r(1)=r0/2

for n=2:10

    r(n)=r(n-1)/2;

end

rn=[r0,r]

n=0:10;

xn=1./(2.^n);

y=xn-rn;

plot(n,y,'.')

xlabel('n');

ylabel('xn-rn');

（2）pn与xn-pn计算值

n=0:10;

xn=1./(2.^n)

 

p0=1;p(1)=0.497;p(2)=3*p(1)/2-p0/2;

for n=3:10

    p(n)=3*p(n-1)/2-p(n-2)/2;

end

pn=[p0,p];

n=xn-pn;

xn-pn生成图片

p0=1;p(1)=0.497;p(2)=3*p(1)/2-p0/2;

for n=3:10

    p(n)=3*p(n-1)/2-p(n-2)/2;

end

pn=[p0,p]

n=0:10;

xn=1./(2.^n);

y=xn-pn;

plot(n,y,'.')

xlabel('n');

ylabel('xn-pn');

（3）qn与xn-qn计算值

n=0:10;

xn=1./(2.^n)

 

q0=1;q(1)=0.497;q(2)=5*q(1)/2-q0;

for n=3:10

    q(n)=3*q(n-1)/2-q(n-2)/2

end

qn=[q0,q];

w=xn-qn;

xn-qn生成图片

q0=1;q(1)=0.497;q(2)=5*q(1)/2-q0;

for n=3:10

    q(n)=3*q(n-1)/2-q(n-2)/2

end

qn=[q0,q]

n=0:10;

xn=1./(2.^n);

y=xn-qn;

plot(n,y,'.')

xlabel('n');

ylabel('xn-qn');

3.实验结果

（1）差分方程近似值情况汇总如下

（2）差分方程误差{xn-rn}{xn-pn}{xn-qn}生成图片

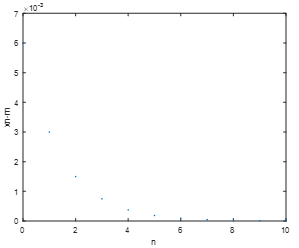
                     图1 {xn-rn}

                  图2 {xn-pn}

                   图3 {xn-qn}