Symbolic Root
syms和sym:定义/声明一个变量
syms x %方法一
x=sym('x') %方法二
解析解
Symbolic Root Finding: solve()
一元一次方程求解示例
求方程式y=x•sin(x)−xy=x•sin(x)-xy=x•sin(x)−x的根,即令y=0y=0y=0求 x 的值
syms x
y = x*sin(x)-x;
solve(y, x)

练习
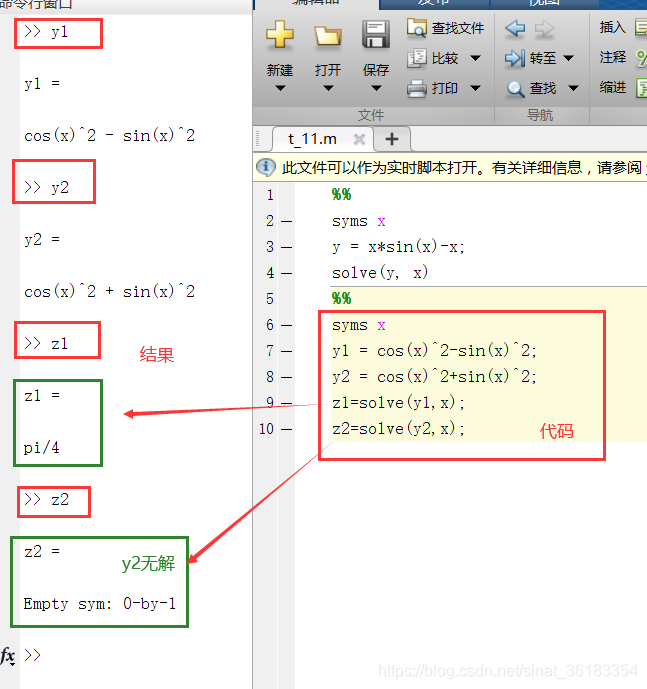
求方程式cos(x)2−sin(x)2=0cos(x)^2-sin(x)^2=0cos(x)2−sin(x)2=0和cos(x)2+sin(x)2=0cos(x)^2+sin(x)^2=0cos(x)2+sin(x)2=0
syms x
y1 = cos(x)^2-sin(x)^2;
y2 = cos(x)^2+sin(x)^2;
z1=solve(y1,x);
z2=solve(y2,x);
二元一次方程求解示例
求解
x−2y=5x-2y=5x−2y=5 且 x+y=6x+y=6x+y=6
syms x y
eq1 = x - 2*y - 5;
eq2 = x + y - 6;
A = solve(eq1,eq2,x,y)
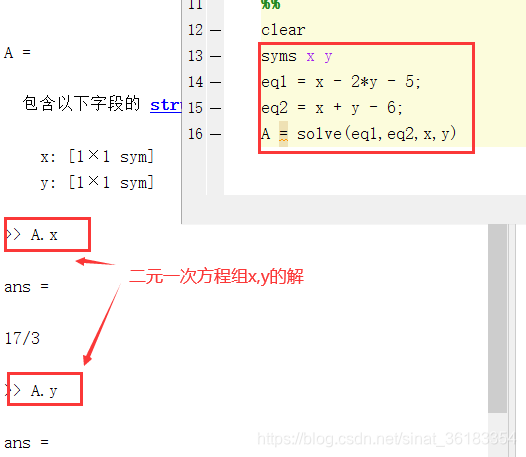
多元方程求解示例
a•x2−b=0a•x^2-b=0a•x2−b=0
syms x a b
solve(a*x^2-b)
syms x a b
solve(a*x^2-b,b)

练习1
求解x的方程式(x−a)2+(y−b)2=r2(x-a)^2+(y-b)^2=r^2(x−a)2+(y−b)2=r2
syms x y a b r
solve((x-a)^2+(y-b)^2-r^2,x)
%%
%更好的一种写法
syms x y a b r;
eq=(x-a)^2+(y-b)^2-r^2;
solve(eq,x)

练习2
求矩阵A的逆,其中A=[a,b;c,d]
注意:矩阵的同行元素之间用空格(或”,”)隔开;矩阵的行与行之间用”;”(或回车符)隔开。
syms a b c d;
A=[a b;c d];
inv(A)

用symbolic的方式解微分:diff()
示例
用symbolic的方式计算y=4x5y=4x^5y





 本文介绍了Matlab中的符号计算功能,包括使用solve()求解方程式,例如一元、二元及多元方程,用diff()求微分,int()求积分,以及fsolve()和fzero()数值求解方法。此外,还涉及多项式解的计算和递归函数的应用。
本文介绍了Matlab中的符号计算功能,包括使用solve()求解方程式,例如一元、二元及多元方程,用diff()求微分,int()求积分,以及fsolve()和fzero()数值求解方法。此外,还涉及多项式解的计算和递归函数的应用。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 1219
1219












