Monte Carlo Integration

最新推荐文章于 2021-12-13 22:59:19 发布

lpty

最新推荐文章于 2021-12-13 22:59:19 发布

阅读量4.3k

点赞数 1

CC 4.0 BY-SA版权

分类专栏：论文阅读文章标签：蒙特卡洛

本文链接：https://blog.youkuaiyun.com/sinat_33741547/article/details/83789151

论文阅读专栏收录该内容

23 篇文章

订阅专栏

本文介绍了蒙特卡罗积分的两种方法：投点法和平均法。通过随机投点和计算落在目标区域内的点的比例，或者在积分区间内随机取点并计算函数值的平均，来估算定积分的值。蒙特卡罗方法提供了一种解决复杂积分问题的有效途径。

引言

Monte Carlo Integration，即蒙特卡罗积分，这是一种很常用的数学方法，原理上也可以很直观的列出来

内容

（一）投点法求定积分

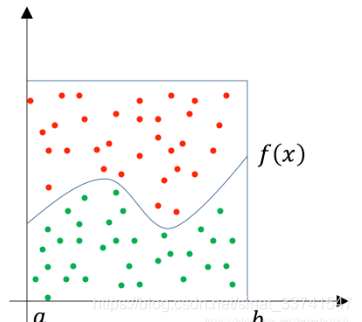
如下图，求函数f(x)从a到b的定积分。用面积为A的矩型罩在函数的积分区间上，随机地向这个矩形框里面投点，其中落在函数f(x)下方的点为绿色，其它点为红色。
统计绿色点的数量占所有点（红色+绿色）数量的比例为r，据此估算出函数f(x)从a到b的定积分为A×r。
在这里插入图片描述
蒙特卡洛方法能得到一个近似值，但前提是投点的方式未为真正的随机，如果必须输入一个模式中的随机数并不像设想的那样是随机数，而却构成一些微妙的非随机模式，那么整个的模拟（及其预测结果）都可能是错的。

（二）平均法求定积分

如下，存在函数f(x)，积分的几何意义就是[a,b]区间内曲线下方的面积：
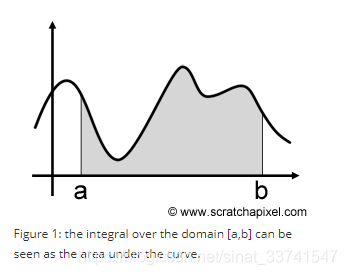
在这里插入图片描述
如果在[a,b]之间随机取一点x，其函数值就是f(x)，那么曲线下方的面积为f(x)×(b−a)，当然很明显这种方法是很不准准确的

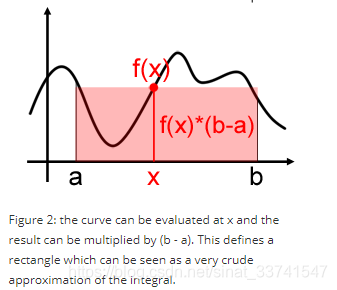
但在[a,b]之间随机取一系列点xi时（xi满足均匀分布），把估算出来的面积取平均来作为积分估计，这样的采样点越来越多，那么估计也就越来越接近真实值
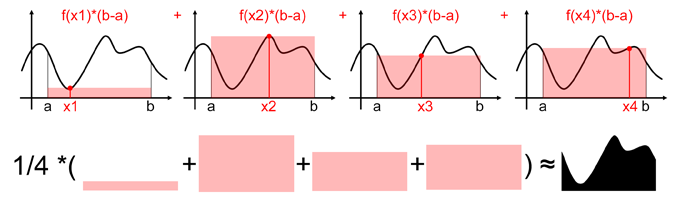
在这里插入图片描述
那么，可以得到公式为： $∫abf(x)dx≈b−aN∑i=1Nf(xi)\int_a^b f(x){\rm d}x\approx\frac{b-a}{N}\sum_{i=1}^Nf(x_i)$