Week 2——Machine learning by Pro.Andrew Ng (cousera)——notebook

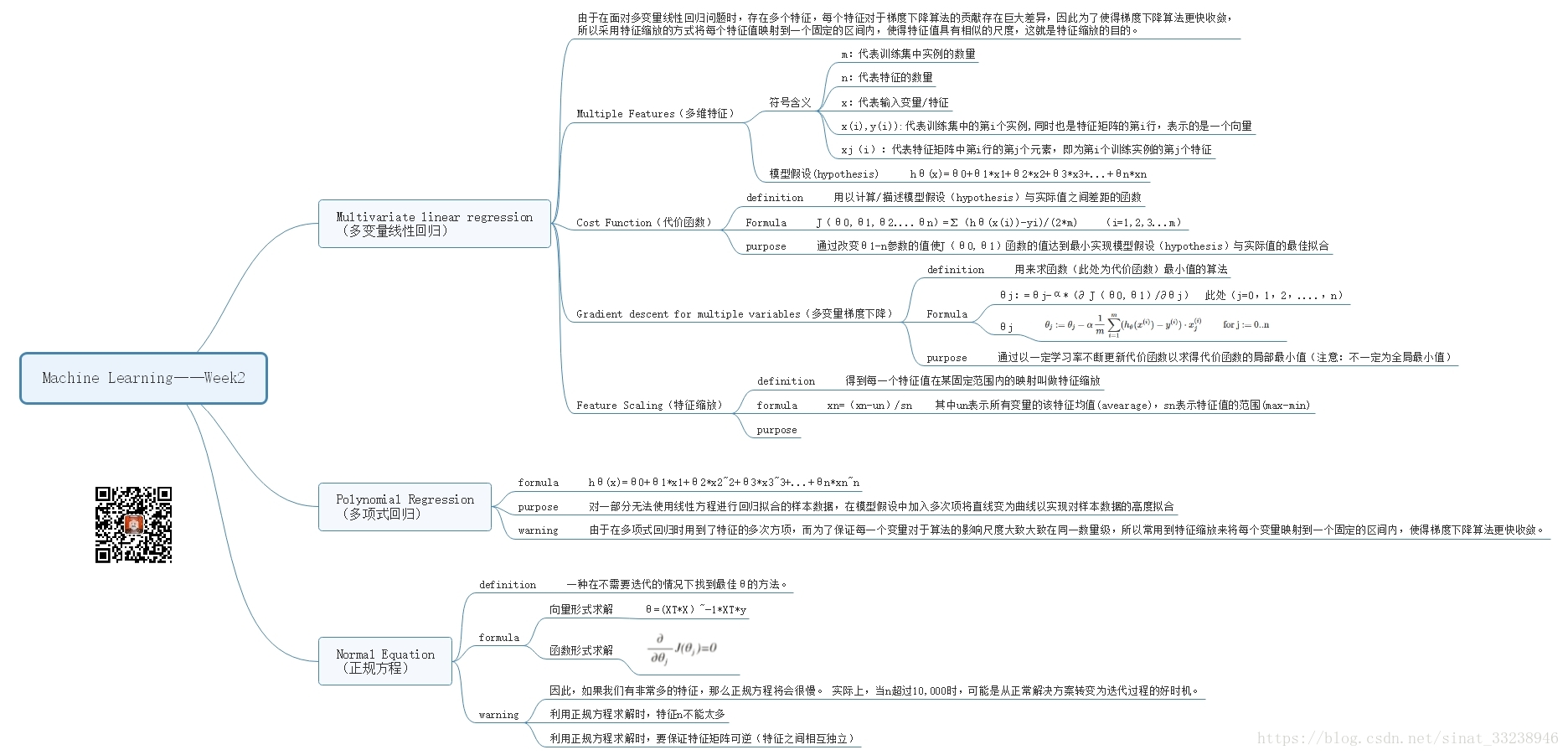
一.概述
$\quad$在学习过Cousera上第一周的课程后，自己也对于机器学习有了一个大致的了解，并理解了最简单机器学习问题——单变量线性回归问题的解决方式。然而实际上在日常的应用中，影响结果的特征因素个数绝不仅仅限于一个，且数据特征与结果的函数关系也不限于线性，因此可想而知，为了解决更为实际的问题，必然可以构建新的更具普适性的假设模型。所以在第二周的课程中介绍了多变量线性回归（Multivariate linear regression），多项式回归（Polynomial Regression）和正规方程（Normal Equation）三种解决机器学习问题可能会用到的方法。

（关于Machine learning by Pro.Andrew Ng 的更多资源请关注图中微信公众号——针知与拙见 获取 ）

• 在第二周的学习中主要应当掌握以下几个主要概念
  
  • 多变量线性回归（Multivariate linear regression）
  • 特征归一化（Feature Normalization ）
  • 多项式回归（Polynomial Regression）
  • 正规方程（Normal Equation）

以及其中概念所对应的函数/向量表达式

1 多变量线性回归的模型表示（Model Representation of Multivariate linear regression）

——$\hat y = h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_3+\theta_4x_4+...+\theta_nx_n$

2 特征归一化（Feature Normalization ）
——$x_i:=\frac{x_i-\mu_i}{s_i}$

3 多项式回归（Polynomial Regression）
—— $\hat y = h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2^2+\theta_3x_3^3+...+\theta_nx_n^n$

4 正规方程（Normal Equation）
—— $\theta=(X^TX)^{-1}X^Ty$

二.多变量线性回归（Multivariate linear regression）

$\quad$在多变量线性回归问题中，我们可以有任意多个输入变量（特征），并通过调整多个变量对于模型假设的贡献（参数$\theta_n$的大小），实现对样本数据最大程度的拟合。

为了实现上述目的，需要了解几个输入变量的定义、多变量线性回归问题所对应的模型假设、代价函数、梯度下降算法以及特征缩放。

首先对多变量线性回归问题中所需要用到的几个输入变量和模型假设进行介绍。

1.模型假设（hypothesis）

m：代表训练集中实例的数量

n=|$x^{(i)}$| : 代表输入变量特征的数目

$x^{(i)}$:代表训练集中的第i个实例

$x_j^{(i)}$：代表特征矩阵中第i行的第j个元素，即为第i个训练实例的第j个特征

hypothesis function——$h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_3+\theta_4x_4+...+\theta_nx_n$

其向量表示形式为——$h_\theta(x)=[\theta_0\quad\theta_1\quad\theta_2...\quad\theta_n]$$\begin{bmatrix}x_0\\x_1\\x_2\\\vdots\\x_n\\\end{bmatrix}$$=\theta^Tx$

2.代价函数（Cost Function）

definition——用以计算/描述模型假设（hypothesis）与实际值之间差距的函数

purpose——通过改变θ1-n参数的值使J（θ0,θ1）函数的值达到最小实现模型假设（hypothesis）与实际值的最佳拟合

函数形式——$J(\theta)=\frac{1}{2m}\sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})^2$

向量形式——$J(\theta)=\frac{1}{2m}(X\theta-\vec y)^T(X\theta-\vec y)$
$\vec y$表示的是所有y值的向量

3.梯度下降（Gradient Descent for Multiple Variables）

$\theta_j:=\theta_j-\alpha\frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} \quad for\quad j:=0...n$

三.特征归一化/规范化（Feature Normalization）——特征缩放和均值归一化

(1)特征缩放（feature scaling）

definition：用来标准化数据特征的范围

purpose:由于在面对多变量线性回归问题时，存在多个特征，每个特征对于梯度下降算法的贡献存在巨大差异，因此为了使得梯度下降算法更快收敛，所以采用特征缩放的方式将每个特征值映射到一个固定的区间内，使得特征值具有相似的尺度，这就是特征缩放的目的。

注意：特征缩放并不是必要的，我们应用它只是为了让梯度下降的速度提高。

method：特征缩放涉及将输入值x除以输入变量的范围（即最大值减去最小值），从而产生仅1的新取值范围。

举例说明：在多变量线性回归处理房价问题时，$x_1$表示房屋面积，$x_2$表示房屋所拥有房间数目。

$x_1=size$ (0-2000 feet^2)
$x_2=$ number of bedrooms(1-5)

在这一实例中，$x_1$的变化范围远大于$x_2$，在遇到这种情况时，就需要应用特征缩放。直接应用特征缩放的方法为：

$x_1=\frac{size(feet^2)}{2000}$

$x_2=\frac{number\quad of\quad bedrooms}{5}$

(2）均值归一化 (mean normalization)

均值归一化是在特征缩放的基础上一个改进，均值归一化是从输入值中减去输入变量的平均值，然后除以输入变量的范围。 其公式表示为：

$x_i:=\frac{x_i-u_i}{s_i}$

在上式中，$u_i$是所有输入变量的平均值，$s_i$是输入变量的范围，即最大值减去最小值。

四.多项式回归（Polynomial Regression）

purpose:对一部分无法使用线性方程进行回归拟合的样本数据，在模型假设中加入多次项将直线变为曲线以实现对样本数据的高度拟合

模型假设(hypothesis function)
——$h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2^2+\theta_3x_3^3+...+\theta_nx_n^n$

注意事项：由于在多项式回归时用到了特征的多次方项，而为了保证每一个变量对于算法的影响尺度大致大致在同一数量级，所以常用到特征缩放来将每个变量映射到一个固定的区间内，使得梯度下降算法更快收敛。

五.正规方程（Normal Equation）

definition:一种在不需要迭代的情况下找到最佳参数(θ)的方法。

向量形式求解
—— $\theta=(X^TX)^{-1}X^Ty$

函数形式求解
——令$\frac{\partial}{\partial\theta_j}J(\theta_j)=0$求出满足条件的参数$\theta$

需要注意的是:

1 如果我们有非常多的特征，那么正规方程将会计算的很慢。 实际上，当n超过10,000时，可能是从正常解决方案转变为迭代过程的好时机。

2 利用正规方程求解时，特征n不能太多

3 利用正规方程求解时，要保证特征矩阵可逆（特征之间相互独立）

---

$\quad$文中部分英文原文取自Pro.Andrew Ng 于cousera上发布的Machine learning 公开课的Week 2 Lecture Notes。其他内容均由个人整理撰写，如需要更多机器学习的学习资源欢迎关注微信公众号：针知与拙见并在后台留言。
[1] https://www.coursera.org/learn/machine-learning/
[2] 微信公众号——针知与拙见