P2437蜜蜂路线[洛谷AC]

题目背景

无

题目描述

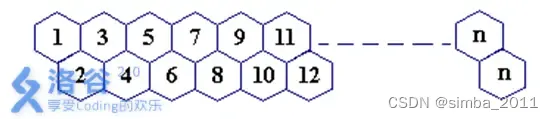
一只蜜蜂在下图所示的数字蜂房上爬动,已知它只能从标号小的蜂房爬到标号大的相邻蜂房,现在问你：蜜蜂从蜂房 m 开始爬到蜂房 n，m<n，有多少种爬行路线？（备注：题面有误，右上角应为n−1）

输入格式

输入 m,n 的值

输出格式

爬行有多少种路线

输入输出样例

输入 #1

1 14

输出 #1

377

说明/提示

对于100%的数据，1≤M,N≤1000

思路

这道题是一道递推题

除此之外，由于超出了int和long long的范围，还需要用到高精度加法。

高精度加法也就是通过模拟同位相加，进位来达到（理论上）接近无穷大的加数允许范围

废话不多说，上代码

AC代码

#include<bits/stdc++.h>//万能头文件
using namespace std;//使用标准命名空间
int a[1002][1002];//定义二维数组
int len = 1；//默认长度为1
void plush(int temp)
{
	for (int i = 0; i <= len - 1; i++)
	{
        //同位相加
		a[temp][i] += a[temp - 1][i] + a[temp - 2][i];
		if (a[temp][i] >= 10)
		{
			a[temp][i + 1] += a[temp][i] / 10;
			a[temp][i] %= 10;
		}
	}
	if (a[temp][len])len++;//进位
}
 
int main()
{
	int m, n;
	cin >> m >> n;
	a[1][0] = 1;
	a[2][0] = 2;//初始化值第二、第三个点
    //递推
	for (int i = 3; i <= n-m; i++)
	{
		plush(i);//调用高精度加法函数
	}
	for (int i = len-1; i>=0; i--)//输出（逆序）
	{
		cout << a[n - m][i];
	}
	cout << endl;//空格的输出
	return 0;
}

撰文不易，点个赞再走吧！

END