题目描述
楼梯有 N 阶,上楼可以一步上一阶,也可以一步上二阶。
编一个程序,计算共有多少种不同的走法。
输入格式
一个数字,楼梯数。
输出格式
输出走的方式总数。
输入输出样例
输入 #1
4
输出 #1
5
说明/提示
- 对于 60% 的数据,N≤50;
- 对于 100% 的数据,1≤N≤5000。
分析
当我们走上一级楼梯时,一共的方案总数就等于前一阶楼梯加上前一阶的前一阶也就是前一阶的前一阶的前一阶的前一阶...加前一阶的前一阶的前一阶的前一阶的前一阶的前一阶...,因此要用到斐波那契数列。fib数列:f[i]=f[i-1]+f[i-2];
除此之外,因为题中的值太大了,所以还要用到高精度加法。
AC代码
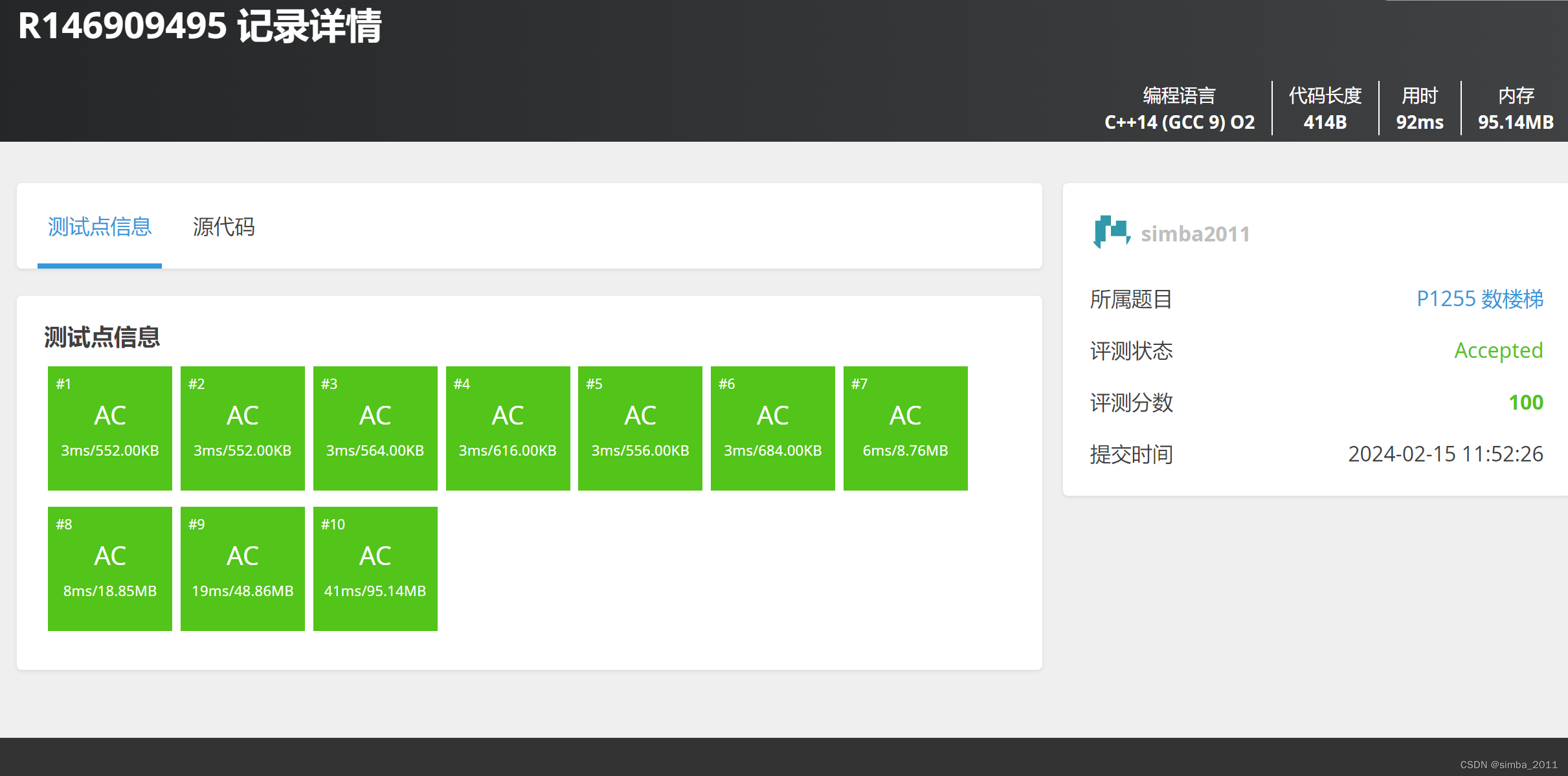
#include<bits/stdc++.h>//万能头文件
using namespace std;//使用标准命名空间
int f[5050][5050],w=1; //f[m][i]表示m阶台阶对应的方法数,i表示数位 ,w表示位数
void hpl(int m) //高精度加法,m表示阶数
{
for(int i=1;i<=w;i++)
f[m][i]=f[m-1][i]+f[m-2][i]; //斐波那契数列
for(int i=1;i<=w;i++) //遍历每一个数位
{
if(f[m][i]>=10) //如果该数位大于等于10则进位
{
f[m][i+1]+=f[m][i]/10;
f[m][i]%=10;
if(f[m][w+1]) //如果进位后还有其它方法则位数加1
w++;
}
}
}
int main()
{
int n;
scanf("%d",&n);//斐波那契数列1,2位
f[1][1]=1; //一阶有一种
f[2][1]=2; //二阶有两种
for(int i=3;i<=n;i++)
hpl(i); //调用高精度加法的函数
for(int i=w;i>=1;i--) //倒序输出
printf("%d",f[n][i]);
return 0;
}







 本文介绍了一种计算从1阶到N阶楼梯的不同走法的编程问题,利用斐波那契数列原理以及高精度加法技术,通过AC代码实现了递推计算阶梯走法总数的过程。
本文介绍了一种计算从1阶到N阶楼梯的不同走法的编程问题,利用斐波那契数列原理以及高精度加法技术,通过AC代码实现了递推计算阶梯走法总数的过程。
















 913
913

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








