二叉树的遍历

本文主要为观看哔哩哔哩视频网站上的王道考研的数据结构的学习笔记，如有侵权，请联系我删除

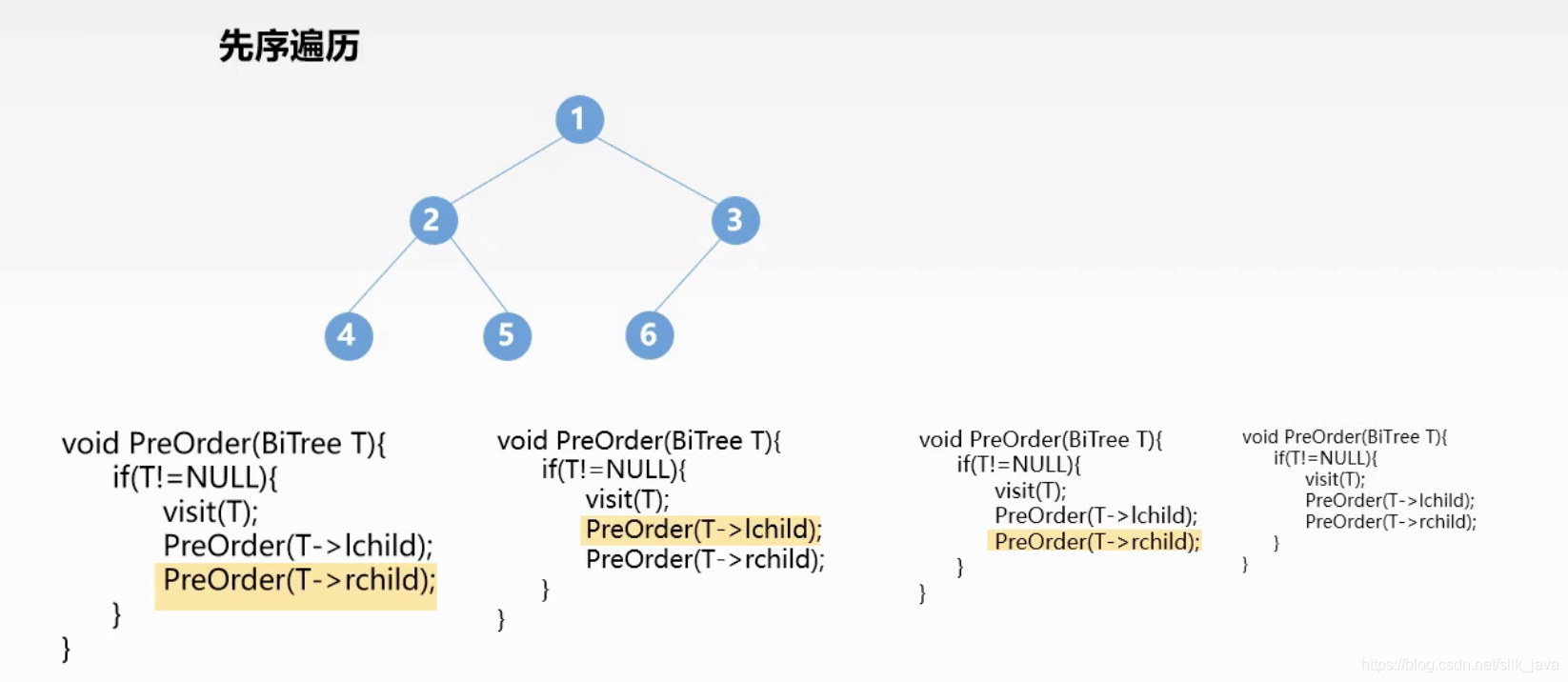
所谓的先中后，都是针对于什么时候访问根结点（父节点）来描述的，而左右两个节点的访问顺序都是先左后右

先序遍历

所谓的递归方法，就是不断复制一个函数，然后对传入的值进行不断的调用这个函数，这个函数结束之后，被传入的值的调用过程就结束，返回上一次没有结束的位置

java代码实现

二叉树节点

package binaryTree;

/**
 * 二叉树节点
 */
public class TreeNode {
    int data;
    TreeNode leftNode;
    TreeNode rightNode;

    public TreeNode(int data) {
        this.data = data;
    }

    public void setLeftNode(TreeNode leftNode) {
        this.leftNode = leftNode;
    }

    public void setRightNode(TreeNode rightNode) {
        this.rightNode = rightNode;
    }


    /**
     * 前序遍历，先取根结点，再取左节点，最后取右节点
     */
    public void frontShow() {
        System.out.print(data + " ");

        if (leftNode != null) {
            leftNode.frontShow();
        }
        if (rightNode != null) {
            rightNode.frontShow();
        }

    }

    /**
     * 中序遍历，先取左节点，再取自己，最后取右节点
     */
    public void middleShow() {
        if (leftNode != null) {
            leftNode.middleShow();
        }
        System.out.print(data + " ");
        if (rightNode != null) {
            rightNode.middleShow();
        }
    }

    /**
     * 后序遍历，先遍历左节点，再遍历右节点，再遍历根节点
     */
    public void afterShow() {

        if (leftNode != null) {
            leftNode.afterShow();
        }
        if (rightNode != null) {
            rightNode.afterShow();
        }
        System.out.println(data);
    }

    //前序查找
    public TreeNode frontSearch(int number) {
        //先比较自己
        if (data == number) {
            return this;
        }
        TreeNode target = null;
        //判断左节点
        if (leftNode != null) {
            target = leftNode.frontSearch(number);
        }
        if (target != null) {
            return target;
        }
        if (rightNode != null) {
            target = rightNode.frontSearch(number);
        }
        return target;


    }

    /**
     * 删除子树
     *
     * @param i 节点值
     */
    public void delete(int i) {
        TreeNode parent = this;
        if (parent.leftNode != null && parent.leftNode.data == i) {
            parent.leftNode = null;
            return;
        }
        if (parent.rightNode != null && parent.rightNode.data == i) {
            parent.rightNode = null;
            return;
        }
        parent = parent.leftNode;
        if (parent != null) {
            parent.delete(i);
        }
        if (parent != null) {
            parent = parent.rightNode;
        }
        if (parent != null) {
            parent.delete(i);

        }
    }
}

二叉树结构

package binaryTree;

/**
 * 二叉树
 */
public class BinaryTree {
    TreeNode root;

    public void setRoot(TreeNode root) {
        this.root = root;
    }


    public void frontShow() {
        if (root != null) {
            root.frontShow();
        }
    }

    public void middleShow() {
        if (root != null) {
            root.middleShow();
        }
    }

    public void afterShow() {
        if (root != null) {
            root.afterShow();
        }
    }

    public TreeNode frontSearch(int number) {
        if (root != null) {
            return root.frontSearch(number);
        }
        return null;
    }

    public void delete(int i) {
        if (root.data == i) {
            root = null;
        } else {
            root.delete(i);

        }
    }
}

测试代码

package binaryTree;

public class Test {
    public static void main(String[] args) {
        BinaryTree tree = new BinaryTree();
        TreeNode root = new TreeNode(1);
        tree.setRoot(root);
        TreeNode leftNode = new TreeNode(2);
        root.setLeftNode(leftNode);
        TreeNode rightNode = new TreeNode(3);
        root.setRightNode(rightNode);
        TreeNode n4 = new TreeNode(4);
        TreeNode n5 = new TreeNode(5);
        TreeNode n6 = new TreeNode(6);
        TreeNode n7 = new TreeNode(7);
        leftNode.setLeftNode(n4);
        leftNode.setRightNode(n5);
        rightNode.setLeftNode(n6);
        rightNode.setRightNode(n7);
        //前序调用
        //tree.frontShow();
        中序遍历
        //tree.middleShow();
        后序遍历
        //tree.afterShow();

        //节点查找
        TreeNode node = tree.frontSearch(2);
        System.out.println(node);

        tree.delete(2);
        tree.frontShow();
    }
}