选择、冒泡、归并、插入及希尔排序

选择排序

选择排序每次遍历一遍数组，找出最小的数，然后跟数组的第一个元素交换。再从剩下的元素中重复此步骤直至数组排序完毕。时间复杂度与输入数据无关，为O(n^2)。

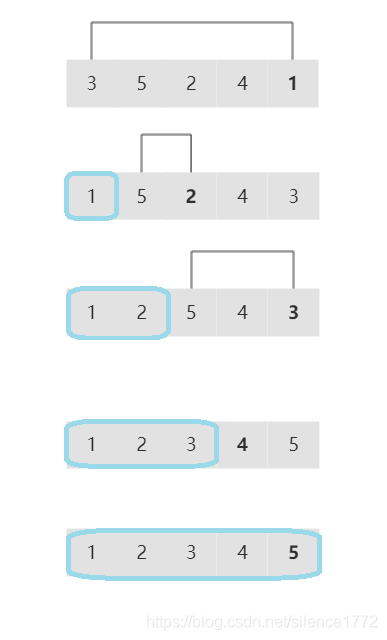
代码：

void SelectSort(vector<int>& a)
{
	int n = a.size();
	for (int i = 0; i < n - 1; ++i)
	{
		int min = i;
		for (int j = i + 1; j < n; ++j)
		{
			if (a[j] < a[i])
				min = j;
		}
		swap(a[i], a[min]);
	}
}

冒泡排序

每次从首元素开始，从左到右交换相邻且逆序的元素，一直交换到尾元素时即完成一轮循环，此时末尾元素即为最大值。接着在除尾元素外的剩余元素中继续上述循环，直至排序完成。时间复杂度为O(n^2)。

可以优化的一点：当在一趟循环中没有元素交换，就说明数组已有序，结束排序。

下图为一趟交换示意图，最后的 5 为排完序部分：

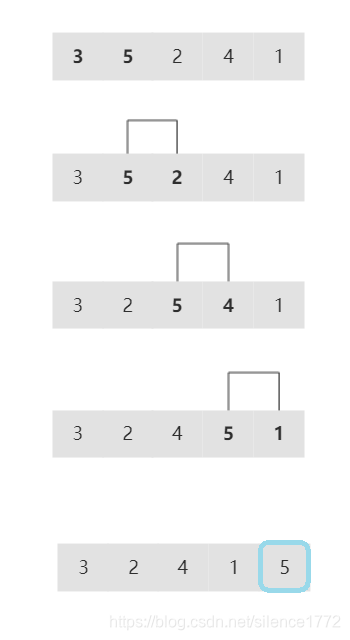
代码：

void BubbleSort(vector<int>& a)
{
	int n = a.size();
	bool has_sorted = false;
	for (int i = n - 1; i > 0 && !has_sorted; --i)
	{
		for (int j = 0; j < i; ++j)
		{
			if (a[j] > a[j + 1])
			{
				has_sorted = false;
				swap(a[j], a[j + 1]);
			}
		}
	}
}

归并排序

主要思想是将数组分成左右两部分，各自排序后再合并起来。子数组排序也是分成两部分，如此递归下去。因其分治策略每次划分的子数组规模都接近相等，故即使在最坏情况下，依然能保持时间复杂度为O(nlogn)。在合并的时候需要一个与原数组大小相等的辅助数组（这里的代码优化为1/2大小），故额外空间复杂度为O(n)。

代码：

// 合并左右两个有序数组
void Merge(vector<int>& a, int low, int mid, int high)
{
	// 临时数组，保存前半部分
	vector<int> tmp(mid - low);
	for (int i = 0; i < tmp.size(); ++i)
		tmp[i] = a[low + i];

	int pa = 0; // 前半部分指针
	int pb = mid; // 后半部分指针
	int pc = low; // 合并指针
	// 开始合并，小的在前
	while (pa < tmp.size() && pb < high)
	{
		if (tmp[pa] <= a[pb])
			a[pc++] = tmp[pa++];
		else
			a[pc++] = a[pb++];
	}
	// 如果剩下的是前半部分，则把这部分填进数组
	// 否则因为剩下的是后半部分，已在原数组且有序，无需处理
	if (pa < tmp.size())
	{
		for (int i = pc; i < high; ++i)
			a[i] = tmp[pa++];
	}
}

void MergeSort(vector<int>& a, int low, int high)
{
	// 单元素自然有序
	if (high - low < 2)
		return;
	int mid = low + (high - low) / 2;
	// 使左右两个数组有序后再合并
	MergeSort(a, low, mid);
	MergeSort(a, mid, high);
	Merge(a, low, mid, high);
}

上面的代码是把逐层递归下来，那么我们直接从最底层开始，合并相邻两个元素形成一个数组，再把这些数组相邻的合并，逐渐往顶层走，就形成了非递归方法。需要注意的是数据最后面没法形成完整两个数组的情况。

非递归版本：

void MergeSort(vector<int>& a)
{
	int n = a.size();
	for (int i = 1; i < n; i += i)
	{
		// 确保最后一组至少有一半
		for (int j = 0; j < n - i; j += 2 * i)
		{
			// 确保最后一组的结尾
			Merge(a, j, j + i, min(j + 2 * i, n));
		}
	}
}

插入排序

每次从未排序部分选取第一个元素插入左边已有序部分，形成新的有序部分，如此循环插入直至整体有序。插入的方法为从右到左相邻逆序即交换，直到合适位置。

在输入数据已有序情况下，只需进行n次比较，时间复杂度为O(n)，若输入完全逆序，则时间复杂度为O(n^2)， 平均复杂度为O(n^2)。

下图左边为已有序部分，将2插入其中。

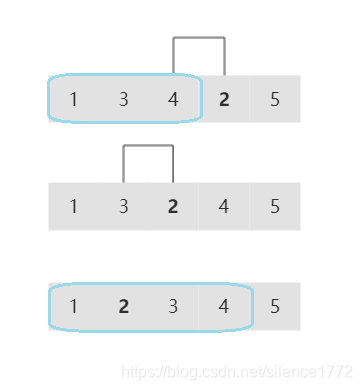
代码：

void InsertSort(vector<int>& a)
{
	int n = a.size();
	for (int i = 1; i < n; ++i)
	{
		for (int j = i; j > 0; --j)
		{
			if (a[j] < a[j - 1])
				swap(a[j], a[j - 1]);
			else
				break;
		}
	}
}

希尔排序

对于大规模的数组，插入排序很慢，因为它只能交换相邻的元素，每次只能将逆序数量减少 1。希尔排序是简单插入排序经过改进之后的一个更高效的版本，也称为缩小增量排序。

它通过交换不相邻的元素，每次可以将逆序数量减少大于 1。随着数组有序性的不断提高，运行时间将会锐减。

希尔排序使用插入排序对间隔 h 的序列进行排序。通过不断减小 h，最后令 h=1，就可以使得整个数组是有序的。

图片来源：https://www.cnblogs.com/chengxiao/p/6104371.html

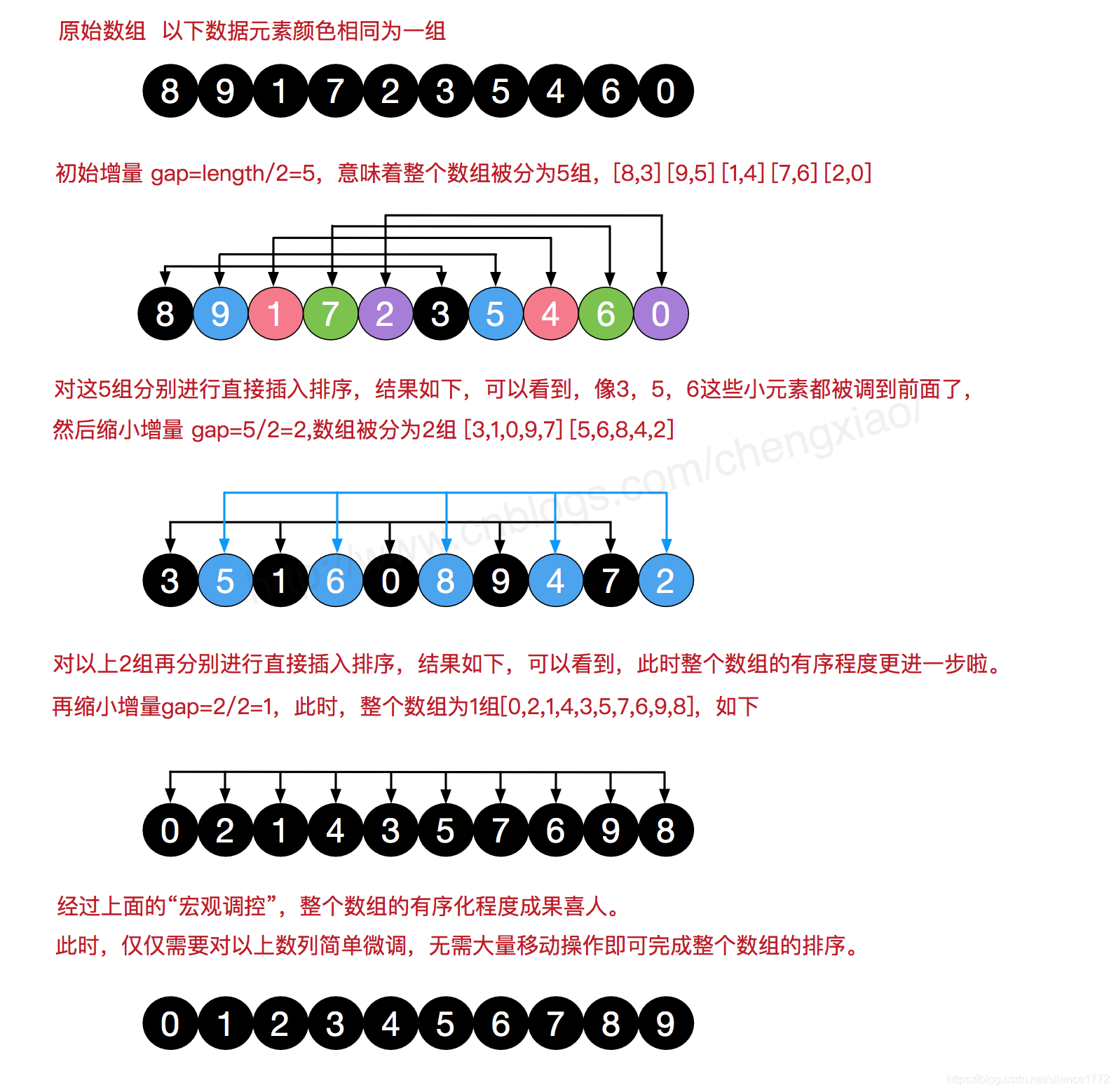
代码：

void ShellSort(vector<int>& a)
{
	int n = a.size();
	int h = 1;
	while (h < n / 3)
	{
		h = h * 3 + 1;
	}// 1 4 13 40...

	while (h >= 1)
	{
		for (int i = h; i < n; ++i)
		{
			for (int j = i; j >= h && a[j] < a[j - h]; j -= h)
			{
				swap(a[j], a[j - h]);
			}
		}
		h = h / 3;
	}
}

希尔排序在最坏情况下时间复杂度为O(n^2) ，但随着逆序对的减少，运行时间会越来越短，最终时间复杂度低于O(n^2)。同时，希尔排序的好坏严重依赖于所选的增量序列。