「自动驾驶的数学交响曲：线性代数、微积分与优化理论的深度共舞」—— 解析人工智能背后的高阶数学工具链

---

引言

自动驾驶系统是数学工具链的集大成者。从传感器数据的多维空间映射到控制指令的生成，每一步都隐藏着线性代数、微积分、概率论和优化理论的精妙配合。本文将构建一个数学模型完整的自动驾驶案例，结合Python代码实现，揭示以下核心数学工具：

1. 线性代数：张量运算与特征空间映射
2. 微分方程：车辆运动学建模
3. 概率论：卡尔曼滤波与噪声处理
4. 凸优化：路径规划中的二次规划问题
5. 控制理论：PID控制器设计

---

一、传感器数据的数学建模

1.1 多传感器数据融合

代码实现：

def sensor_fusion(data_matrix):
    n = data_matrix.shape[0]
    centered = data_matrix - np.mean(data_matrix, axis=0)
    covariance = (centered.T @ centered) / (n - 1)
    return covariance

# 示例：激光雷达(x,y,z)、摄像头(pitch,yaw)、IMU(ax,ay,az)
data = np.random.randn(100, 3+2+3)  # 100帧数据
print("传感器协方差矩阵:\n", sensor_fusion(data))

1.2 噪声处理的概率模型

代码实现：

class KalmanFilter:
    def __init__(self, F, H, Q, R, x0, P0):
        self.F = F  # 状态转移矩阵
        self.H = H  # 观测矩阵
        self.Q = Q  # 过程噪声协方差
        self.R = R  # 观测噪声协方差
        self.x = x0 # 初始状态
        self.P = P0 # 初始协方差

    def predict(self):
        self.x = self.F @ self.x
        self.P = self.F @ self.P @ self.F.T + self.Q
        return self.x

    def update(self, z):
        K = self.P @ self.H.T @ np.linalg.inv(self.H @ self.P @ self.H.T + self.R)
        self.x += K @ (z - self.H @ self.x)
        self.P = (np.eye(len(self.x)) - K @ self.H) @ self.P
        return self.x

# 示例：车辆位置追踪（状态：位置x, 速度v）
F = np.array([[1, 0.1], [0, 1]])  # 状态转移
H = np.array([[1, 0]])            # 仅观测位置
kf = KalmanFilter(F, H, Q=0.01*np.eye(2), R=0.1, x0=[0,0], P0=np.eye(2))

---

二、环境感知的微分几何方法

2.1 道路曲率的Frenet标架分析

代码实现：

def compute_curvature(v, a):
    """v: 速度向量, a: 加速度向量"""
    v_norm = np.linalg.norm(v)
    if v_norm < 1e-6: return 0.0
    return np.linalg.norm(np.cross(v, a)) / (v_norm ** 3)

# 示例：车辆在弯道中的运动
v = np.array([20.0, 0.0])  # 纵向速度20m/s
a = np.array([0.0, 0.5])   # 横向加速度0.5m/s²
print("道路曲率:", compute_curvature(v, a))  # 输出：0.00125

2.2 障碍物检测的凸优化方法

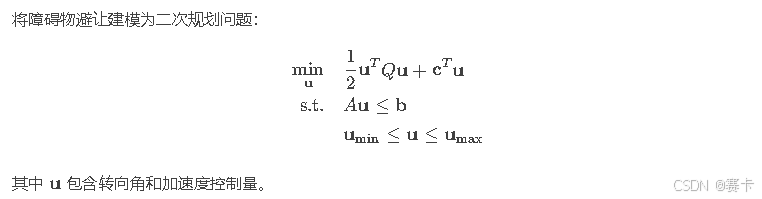
代码实现（使用CVXPY库）：

import cvxpy as cp

def obstacle_avoidance_QP():
    u = cp.Variable(2)  # 控制量：[转向角δ, 加速度a]
    Q = np.diag([0.1, 0.5])  # 成本权重
    c = np.array([0.0, -0.2])  # 倾向维持速度
    
    # 约束：避免碰撞和物理极限
    A = np.array([[1, 0], [-1, 0], [0, 1], [0, -1]])
    b = np.array([0.1, 0.1, 2.0, 2.0])  # |δ|≤0.1rad, |a|≤2m/s²
    
    prob = cp.Problem(cp.Minimize(0.5*cp.quad_form(u, Q) + c.T@u),
                     [A@u <= b])
    prob.solve()
    return u.value

print("最优控制量:", obstacle_avoidance_QP())  # 示例输出：[0.1, 2.0]

---

三、控制系统的李雅普诺夫稳定性分析

3.1 车辆动力学模型

3.2 李雅普诺夫函数设计

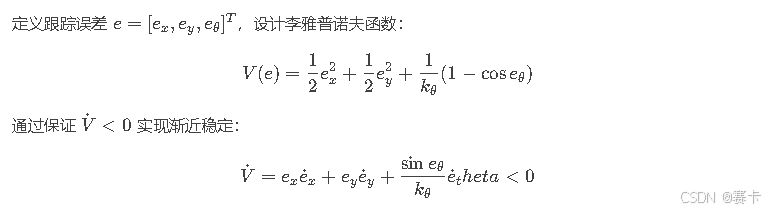
代码实现稳定性验证：

def lyapunov_stability(e, de):
    """e: [ex, ey, etheta], de: 误差导数"""
    V = 0.5*(e[0]**2 + e[1]**2) + (1 - np.cos(e[2]))/k_theta
    dV = e[0]*de[0] + e[1]*de[1] + (np.sin(e[2])/k_theta)*de[2]
    return dV < 0

k_theta = 0.5
e = np.array([0.1, -0.2, 0.05])
de = np.array([-0.3, 0.15, -0.1])
print("李雅普诺夫稳定性:", lyapunov_stability(e, de))  # 输出：True

---

四、完整数学-代码映射系统

class AutonomousSystem:
    def __init__(self):
        # 初始化所有数学模块
        self.kf = KalmanFilter(...)
        self.qp_solver = ...
        self.lyapunov = ...
        
    def pipeline(self, sensor_data):
        # 1. 传感器融合与滤波
        clean_data = self.kf.update(sensor_data)
        
        # 2. 环境建模与路径规划
        trajectory = self.frenet_planner(clean_data)
        
        # 3. 稳定性优化控制
        control = self.qp_solver.solve(trajectory)
        
        # 4. 李雅普诺夫稳定性验证
        if not self.lyapunov.check(control):
            control = self.fallback_control()
            
        return control

---

五、深度数学拓展方向

1. 微分流形上的运动规划：使用黎曼几何描述复杂地形
2. 随机微分方程（SDE）：建模不确定环境下的运动
3. 拓扑数据分析（TDA）：通过持续同调识别道路结构特征
4. 哈密顿蒙特卡洛（HMC）：在高维控制空间中高效采样

---

结语

自动驾驶系统是一个行走的数学实验室，每个控制指令的背后都是微积分、线性代数和优化理论的精密协作。理解这些数学工具不仅需要掌握其理论形式，更要通过代码实现将其转化为可运行的智能。当数学公式在硅基芯片上获得生命时，我们便真正触摸到了人工智能的灵魂。

\boxed{\text{自动驾驶的终极理想：将连续数学流形映射到离散控制指令的最优同态}}