代码随想录算法训练营Day2

最新推荐文章于 2025-12-10 19:44:03 发布

原创最新推荐文章于 2025-12-10 19:44:03 发布 · 110 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #leetcode #数据结构

Leetcode个人刷题总结专栏收录该内容

40 篇文章

订阅专栏

本文介绍了三个编程问题的解决方案：1) 有序数组的平方，使用双指针法实现高效排序；2) 长度最小的子数组，通过双指针找到满足条件的最小子数组；3) 螺旋矩阵II，通过循环处理边界构建螺旋矩阵。每道题都提供了详细的解题思路和代码实现，重点探讨了算法的时间复杂度和空间效率。

977. 有序数组的平方

给你一个按非递减顺序排序的整数数组 nums，返回每个数字的平方组成的新数组，要求也按非递减顺序排序。

示例 1：

输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]
示例 2：

输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

提示：

1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 已按非递减顺序排序

解题思路：方法一：平方后快排序。

方法二：利用双指针，i指向起始位置，j指向终止位置。

定义一个新数组result，和A数组一样的大小，让k指向result数组终止位置。

如果A[i] * A[i] < A[j] * A[j] 那么result[k--] = A[j] * A[j]; 。

如果A[i] * A[i] >= A[j] * A[j] 那么result[k--] = A[i] * A[i]; 。

个人代码

class Solution {
    public int[] sortedSquares(int[] nums) {
        int i = 0; 
        int j = nums.length -1;
        int[] re = new int[nums.length];// 定义平方后新排序的数组
        int k = nums.length -1; //初始化最大平方值的数组下标；
        while(i <= j){
            if(nums[i] * nums[i] <= nums[j] * nums[j]){
                re[k] = nums[j] * nums[j];
                k--;
                j--;
                  
            }else{
                 re[k] = nums[i] * nums[i];
                 k--;
                 i++;
                }
            }
            return re;
        }
    }

总结：方法一最容易想到，且易实现，但是时间空间复杂度高 O（nlgn）；方法二，利用双指针思想，快速实现排序，时间空间复杂度为O（n).

209. 长度最小的子数组

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2：

输入：target = 4, nums = [1,4,4]
输出：1
示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

解题思路：

方法一：两个for循环，然后不断的寻找符合条件的子序列，时间复杂度是O(n^2)

方法二: 双指针，先移动终止指针，找出子集和大于等于target，然后移动初始指针位置，找出最小长度的子集。

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int i = 0;//起始位置初始化
        int sum = 0;
        int sublength = 0;
        int res = Integer.MAX_VALUE;//定义一个无穷大值
        for(int j = 0; j < nums.length; j++){
            sum += nums[j];//计算终止位置的集合元素的和
            while(sum >= target){//不可以用for
                sublength = j - i + 1;//子集的长度
                res = Math.min(res, sublength);
                sum = sum - nums[i];//移动起始位置，找出最小长度子集
                i++;
            }
        }
        return res == Integer.MAX_VALUE ? 0 : res;

    }
}

59. 螺旋矩阵 II

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：

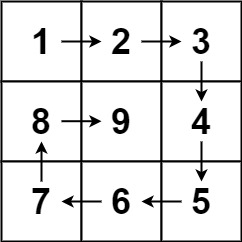
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：

输入：n = 1
输出：[[1]]


解题思路:题目本身思路很简单，就是对应处理每次循环的四条边，难点在于边界的处理以及每次循环变量的初始化以及循环后处理。

class Solution {
    public int[][] generateMatrix(int n) {
        int x = 0;//横纵坐标初始化
        int y = 0;//纵坐标初始化
        int k = 0;//循环初始化
        int count = 1; // 数值初始化
        int i, j;
        int[][] nums = new int[n][n];
        while(k++ < n / 2){// k++只能写在这里？
            for(j = y; j < n - k; j++){// 上边界遍历
                nums[x][j] = count++;
            }
            for(i = x; i < n - k; i++){// 右边界遍历
                nums[i][j] = count++;
            }
            for(; j >= k; j--){//下边界遍历
                nums[i][j] = count++;
            }
            for(; i >= k; i--){//左边界遍历
                nums[i][j] = count++;
            }
            x++;
            y++;
         
        }
        if(n % 2 == 1){
            nums[x][y]= count;
        }
        return nums;
    }
}

总结：刷题第二天，最后一题螺旋矩阵对于循环次数的初始化以及增量k的处理还不是特别理解。为什么k++只能写在循环条件内，后续需思考和理解。