【力扣 - 对称二叉树】

题目描述

给你一个二叉树的根节点 root ， 检查它是否轴对称。

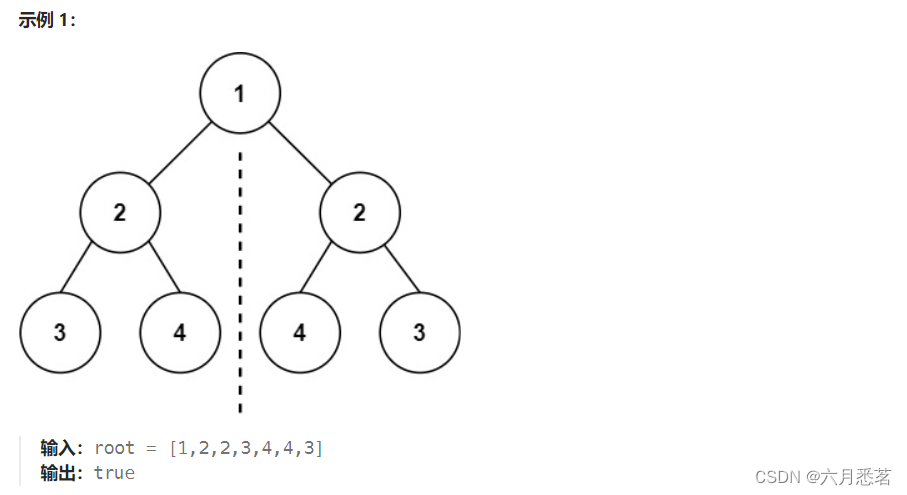
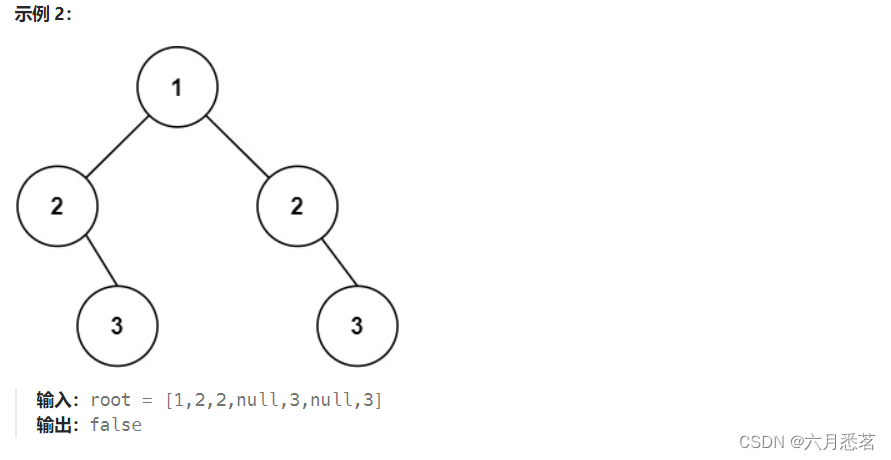
提示：

树中节点数目在范围 [1, 1000] 内

-100 <= Node.val <= 100

题解1

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
// Helper function to check if two trees are symmetric
bool check(struct TreeNode* p, struct TreeNode* q)
{
    // If both nodes are NULL, they are symmetric
    if(p == NULL && q == NULL)
        return true;
    
    // If one node is NULL and the other is not, they are not symmetric
    if(p == NULL || q == NULL)
        return false;
    
    // If the values of the nodes are equal, recursively check their children
    if(p->val == q->val)
        return check(p->left, q->right) && check(p->right, q->left);
    else
        return false;
}

// Main function to check if a binary tree is symmetric
bool isSymmetric(struct TreeNode* root){
    // Call the helper function with the root node to check symmetry
    return check(root, root);
}

题解2

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool isSymmetric(struct TreeNode* root){
    if (root == NULL) return true; // If the root is NULL, it is symmetric
    return fun(root->left, root->right); // Check symmetry of left and right subtrees
}

int fun(struct TreeNode* l_root, struct TreeNode* r_root){
    if (l_root == NULL && r_root == NULL) return true; // If both nodes are NULL, they are symmetric
    if (l_root == NULL || r_root == NULL) return false; // If one node is NULL and the other is not, they are not symmetric

    return (l_root->val == r_root->val) && // Check if values of nodes are equal
           fun(l_root->left, r_root->right) && // Recursively check left of left subtree with right of right subtree
           fun(l_root->right, r_root->left); // Recursively check right of left subtree with left of right subtree
}