【力扣 - 二叉树的最大深度】

题目描述

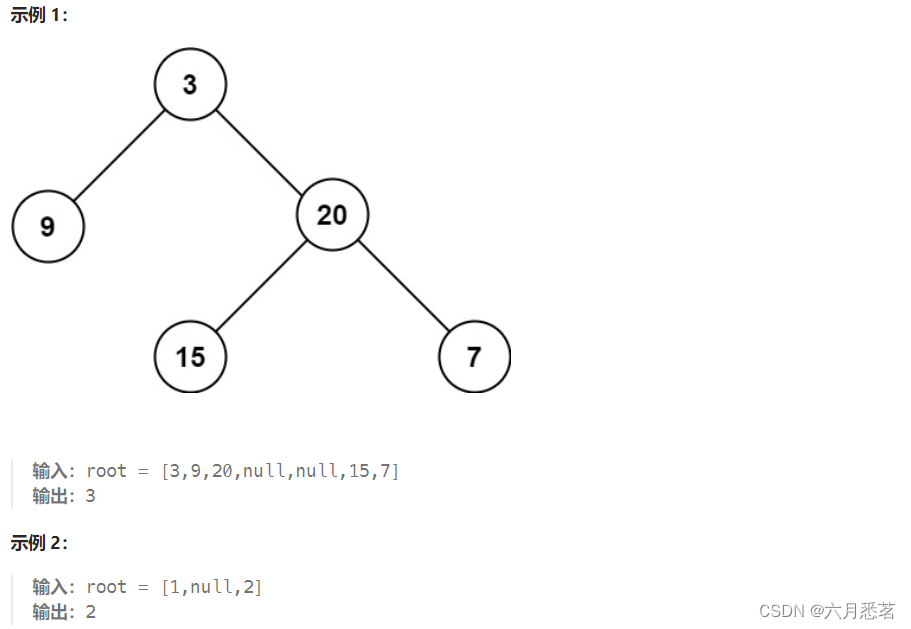
给定一个二叉树 root ，返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

提示：

树中节点的数量在 [0, 10^4] 区间内。

-100 <= Node.val <= 100

方法一：深度优先搜索

思路与算法

如果我们知道了左子树和右子树的最大深度 l 和 r，那么该二叉树的最大深度即为

max(l,r)+1

而左子树和右子树的最大深度又可以以同样的方式进行计算。因此我们可以用「深度优先搜索」的方法来计算二叉树的最大深度。具体而言，在计算当前二叉树的最大深度时，可以先递归计算出其左子树和右子树的最大深度，然后在 O(1)时间内计算出当前二叉树的最大深度。递归在访问到空节点时退出。

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
// Function to calculate the maximum depth of a binary tree
int maxDepth(struct TreeNode *root) {
    // If the root is NULL, return 0 (base case for empty tree)
    if (root == NULL) {
        return 0;
    }
    
    // Recursively calculate the maximum depth of the left and right subtrees
    // Find the maximum depth between the left and right subtrees using fmax
    return fmax(maxDepth(root->left), maxDepth(root->right)) + 1;
}

复杂度分析

时间复杂度：O(n)，其中 n 为二叉树节点的个数。每个节点在递归中只被遍历一次。

空间复杂度：O(height)，其中 height 表示二叉树的高度。递归函数需要栈空间，而栈空间取决于递归的深度，因此空间复杂度等价于二叉树的高度。

方法二：广度优先搜索

思路与算法

我们也可以用「广度优先搜索」的方法来解决这道题目，但我们需要对其进行一些修改，此时我们广度优先搜索的队列里存放的是「当前层的所有节点」。每次拓展下一层的时候，不同于广度优先搜索的每次只从队列里拿出一个节点，我们需要将队列里的所有节点都拿出来进行拓展，这样能保证每次拓展完的时候队列里存放的是当前层的所有节点，即我们是一层一层地进行拓展，最后我们用一个变量 ans 来维护拓展的次数，该二叉树的最大深度即为 ans。

代码

// Define a structure for a node in the queue
struct QueNode {
    struct TreeNode *p;  // Pointer to a TreeNode
    struct QueNode *next;  // Pointer to the next QueNode
};

// Function to initialize a QueNode with a TreeNode
void init(struct QueNode **p, struct TreeNode *t) {
    (*p) = (struct QueNode *)malloc(sizeof(struct QueNode));  // Allocate memory for a QueNode
    (*p)->p = t;  // Assign the TreeNode t to the QueNode's p
    (*p)->next = NULL;  // Set the next pointer of the QueNode to NULL
}

// Function to calculate the maximum depth of a binary tree using a queue-based approach
int maxDepth(struct TreeNode *root) {
    // If the root is NULL, return 0 (base case for empty tree)
    if (root == NULL) return 0;
    
    // Initialize QueNode pointers for left and right nodes
    struct QueNode *left, *right;
    
    // Initialize the queue with the root node
    init(&left, root);
    right = left;
    
    // Initialize variables for answer, size of the queue, and temporary counter
    int ans = 0, sz = 1, tmp = 0;
    
    // Process nodes in the queue to calculate the maximum depth
    while (left != NULL) {
        tmp = 0;  // Reset the temporary counter
        
        // Process nodes at the current level
        while (sz > 0) {
            // Add left child to the queue if it exists
            if (left->p->left != NULL) {
                init(&right->next, left->p->left);
                right = right->next;
                tmp++;
            }
            
            // Add right child to the queue if it exists
            if (left->p->right != NULL) {
                init(&right->next, left->p->right);
                right = right->next;
                tmp++;
            }
            
            // Move to the next node in the queue and decrement the size counter
            left = left->next;
            sz--;
        }
        
        // Update the queue size with the count of nodes at the next level
        sz += tmp;
        
        // Increment the depth counter
        ans++;
    }
    
    // Return the maximum depth of the binary tree
    return ans;
}

复杂度分析

时间复杂度：O(n)，其中 n 为二叉树的节点个数。与方法一同样的分析，每个节点只会被访问一次。
空间复杂度：此方法空间的消耗取决于队列存储的元素数量，其在最坏情况下会达到 O(n)。

作者：力扣官方题解
链接：https://leetcode.cn/problems/maximum-depth-of-binary-tree/solutions/349250/er-cha-shu-de-zui-da-shen-du-by-leetcode-solution/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。