【opencv学习笔记】030 之凸包之Graham扫描法与Jarvis步进法详解

最新推荐文章于 2025-05-25 09:37:29 发布

水亦心

最新推荐文章于 2025-05-25 09:37:29 发布

阅读量3.9k

点赞数 7

分类专栏： opencv 文章标签： Graham扫描法 Jarvis步进法凸包 drawContours

本文链接：https://blog.youkuaiyun.com/shuiyixin/article/details/104625013

版权

opencv 专栏收录该内容

54 篇文章

订阅专栏

本文深入探讨了OpenCV中的凸包检测技术，包括概念解析、两种主要算法（Graham扫描法和Jarvis步进法）的原理及应用，同时提供了详细的API说明和代码实例，帮助读者理解和实践凸包检测。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、前言

继续更新有关于opencv的基础博客，即将更新完毕，想想有点开心呢！

如果想看其他有关于OpenCV学习方法介绍、学习教程、代码实战、常见报错及解决方案等相关内容，可以直接看我的OpenCV分类：

【OpenCV系列】：https://blog.youkuaiyun.com/shuiyixin/article/category/7581855

如果你想了解更多有关于计算机视觉、OpenCV、机器学习、深度学习等相关技术的内容，想与更多大佬一起沟通，那就扫描下方二维码加入我们吧！

二、凸包

1、概念

凸包（Convex Hull）本身是一个计算几何（图形学）中的概念。

首先我们先来理解一下凸包。

从字面意思来看，凸包，就是两点：

（1）凸：得到的结果是一个凸出的形状，可以理解为一个凸多边形。

（2）包：包围图像中的所有东西。

举个例子，大家就能够更加直观的理解了：

我们也可以理解为这个是一个平面，上面钉了很多钉子，然后用一根细线或者橡皮筋把他包围起来，包围的这一周就是凸包。

当然，这个是对于二维平面，我们通过二维平面来理解凸包，那我们现在给出在多维平面（向量空间）中的定义：

在一个实数向量空间V中，对于给定集合X，所有包含X的凸集的交集S被称为X的凸包。X的凸包可以用X内所有点(X1，...Xn)的凸组合来构造.

2、凸包查找算法

我们要找到凸包，有两种算法。

（1）Graham扫描法

（2）Jarvis步进法

对于下面的这些点，我们使用这两种凸包算法来求解凸包。

1.Graham扫描法

首先我们要先找到凸包中最下面的那个点（如果有多个，选择第一个）。所以，我们的A点是作为我们找到的第一个点，然后做A点到其他所有点的向量

按照所有向量与x轴中夹角，然后将其排序为：

A, B, C, D, E, F, G, H

找夹角最小的点，如果有多个，选择与A距离最远的，所以我们找到点C，这样，我们连接点C，就找到了第一条连线，然后我们将ABC三个点压入栈中：

然后我们以点C为起点，做与其他点的向量，注意，因为ABC使用过，已经压入栈中，所以，不用再与AB两点做向量。

我们发现CD向量与X轴的夹角的角度最小，所以，我们将点D压入栈中，找到了第二条直线：

然后再以点D作为起点，做相同的操作，我们发现，DF向量与X轴的夹角最小。我们将点F压入栈中，找到了第三条直线，因为E在F前面，所以E点删除掉。

上面这个在具体实现过程中，要先做DE角度判断，因为是第一个，就是当前最大，所以压入栈中，当判断DF时，DF与X轴的夹角更小，所以我们让E出栈，就是删除了E点，F点入栈。然后判断GH，没有比DF更小的了，结束。

现在我们还有GH两个点，FG与X轴夹角更小，G点入栈，找到了第四条直线。

最后只剩下一个点，连接GH，HA，凸包就找到了。

2.Jarvis步进法

网上比较少有Jarvis步进法的详细讲解，我也是找了一些讲解的方法，然后结合自己的理解，讲一下这个方法。如果理解不对，还希望大家批评指正。

Jarvis步进法又叫包裹法，就是一步一步把所有的点都包裹进去。

我们考虑假设我们有一个很长的棍子，绕着一个不规则的多边形转动，每稳定一次，我们记录一次棍子的位置，当转动到以前记录的位置的时候，我们发现，我们就能得到这个不规则多边形的凸包：

假设我们是哈利波特的传人，我们坐在这根棍子上，棍子在AB上的时候，我们面朝AB向量指向的方向。那我们每次跟随棍子转动的时候，我们会发现，除了在棍子上的点，其余的点，都在我们身体的左侧，当我们转动一周后，就相当于把所有的点包裹起来了。

接下来我们来讲一下这种算法的思想

首先我们要先找到凸包中最下面的那个点（如果有多个，选择第一个），当然也有的说是最左边的那个点，这个其实没有关系，只是起点不同，重点是我们的思想。所以，我们的A点是作为我们找到的第一个点，然后做A点到其他所有点的向量：

我们找一个能让所有点都在向量方向左侧的模最大的向量（向量长度最长），也就是我们找到了C点。我们将AC连起来，然后将B,C点删除掉。

然后我们以点C为起点，做与剩余点的向量（包括CA向量）：

我们找一个能让所有点都在向量方向左侧的模最大的向量（向量长度最长），我们发现是D点，将CD连起来，然后将D点删除：

然后再以点D作为起点，做与剩余点的向量，我们找一个能让所有点都在向量方向左侧的模最大的向量（向量长度最长），我们发现是F点，将DF连起来，然后将F点删除：

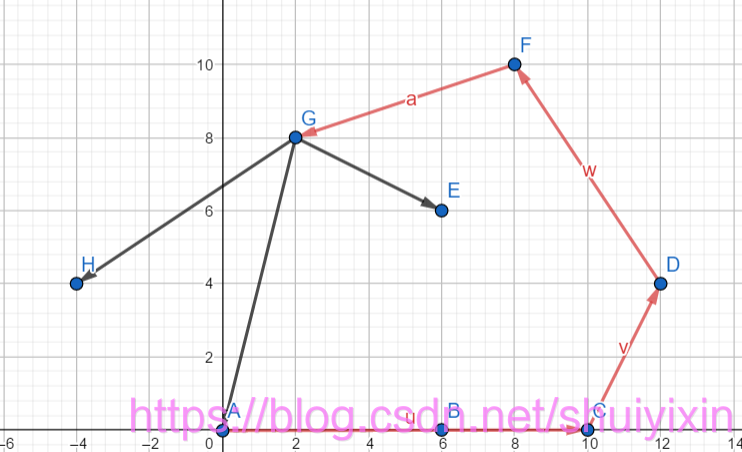
然后再以点F作为起点，做与剩余点的向量，我们找一个能让所有点都在向量方向左侧的模最大的向量（向量长度最长），我们发现是G点，将FG连起来，然后将G点删除：

然后再以点G作为起点，做与剩余点的向量，我们找一个能让所有点都在向量方向左侧的模最大的向量（向量长度最长），我们发现是H点，将GH连起来，然后将H点删除：

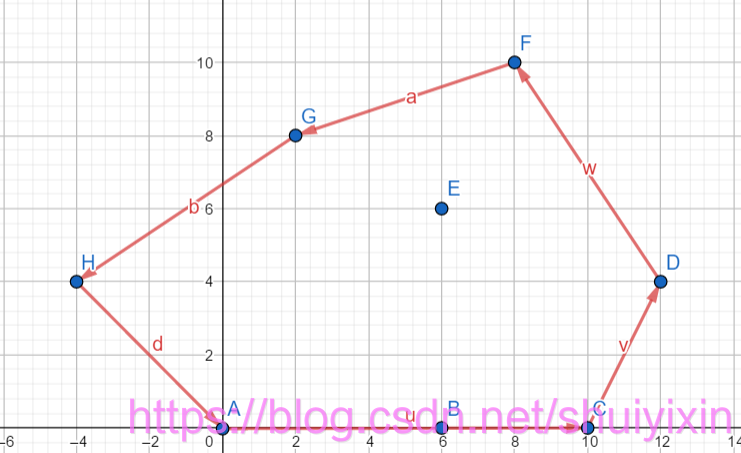
然后再以点H作为起点，做与剩余点的向量，我们找一个能让所有点都在向量方向左侧的模最大的向量（向量长度最长），我们发现是A点，将HA连起来，因为A点是起始点，凸包绘制完毕。

3、凸包API

接下来我们讲一下绘制轮廓的API。

void drawContours( 
    InputArray points, 
    OutputArray hull,
    bool clockwise = false,
    bool returnPoints = true 
);

函数参数含义如下：

（1）InputArray类型的points，输入二维点集，存储在std：：vector或Mat中。

（2）OutputArray类型的hull，输出凸包。它可以是索引的整数向量，也可以是点的向量。

（3）bool类型的clockwise，方向标志。如果为真，则输出凸包将顺时针方向。否则，它是逆时针方向的。假定坐标系的X轴指向右侧，Y轴指向上方。

（4）bool类型的returnPoints，操作标志。对于矩阵，当标志为真时，函数返回凸壳点。否则，返回凸壳点的索引。

这个API和昨天我们讲的轮廓绘制是类似的不同的是参数，凸包可以理解为不是那么太标准的轮廓。

4、代码展示

#include<iostream>
#include<opencv2/opencv.hpp>

using namespace std;
using namespace cv;

Mat src, src_gray, dst;
const char* input_win = "【输入图像】";
const char* output_win = "【输出图像】";
const char* trackbar_title = "Threshold:";
int threshold_value = 100;
int threshold_max = 255;
RNG rng(12345);

void Threshold_Callback(int, void*);

int main()
{
	src = imread("E:/个人/学习/编程/C++/CPlusPlusTestProgram/LearnOpenCV/image/ConvexHull1.png");
	if (!src.data)
	{
		cout << "could not load image !";
		waitKey(0);
		return -1;
	}
	namedWindow(input_win, CV_WINDOW_AUTOSIZE);
	namedWindow(output_win, CV_WINDOW_AUTOSIZE);
	imshow(input_win, src);
	cvtColor(src, src_gray, CV_BGR2GRAY);
	blur(src_gray, src_gray, Size(3, 3));

	createTrackbar(trackbar_title, output_win, &threshold_value, threshold_max, Threshold_Callback);
	Threshold_Callback(0, 0);

	waitKey(0);
	return 0;
}


void Threshold_Callback(int, void*) {
	Mat src_copy = src.clone();
	Mat threshold_output;
	vector<vector<Point> > contours;
	vector<Vec4i> hierarchy;

	threshold(src_gray, threshold_output, threshold_value, 255, THRESH_BINARY);

	findContours(threshold_output, contours, hierarchy, CV_RETR_TREE, CV_CHAIN_APPROX_SIMPLE, Point(0, 0));

	vector<vector<Point> >hull(contours.size());
	for (int i = 0; i < contours.size(); i++)
	{
		convexHull(Mat(contours[i]), hull[i], false);
	}

	//Mat drawing = Mat::zeros(threshold_output.size(), CV_8UC3);
	for (int i = 0; i< contours.size(); i++)
	{
		Scalar color = Scalar(rng.uniform(0, 255), rng.uniform(0, 255), rng.uniform(0, 255));
		//drawContours(drawing, contours, i, color, 2, 8, vector<Vec4i>(), 0, Point());
		drawContours(src, hull, i, color, 2, 8, vector<Vec4i>(), 0, Point());
	}

	imshow(output_win, src);
}