(done) 什么是马尔可夫链？Markov Chain

参考视频1：https://www.bilibili.com/video/BV1ko4y1P7Zv/?spm_id_from=333.337.search-card.all.click&vd_source=7a1a0bc74158c6993c7355c5490fc600

参考视频2：https://www.bilibili.com/video/BV1xg4y1K7z4/?spm_id_from=333.788&vd_source=7a1a0bc74158c6993c7355c5490fc600

参考视频3：https://www.bilibili.com/video/BV1Fu411a7C2/?spm_id_from=pageDriver&vd_source=7a1a0bc74158c6993c7355c5490fc600

参考视频4：https://www.bilibili.com/video/BV1HX4y1t7Vy/?spm_id_from=pageDriver&vd_source=7a1a0bc74158c6993c7355c5490fc600

---

如下图所示，马尔可夫链条实际上就是 “状态机”，只不过状态机里不同状态之间的边上是 “概率”
马尔可夫链有一个非常好的性质，那就是：所有 next state 都只和 current state 有关
所以，计算概率的时候，条件只有当前状态

一个很自然的想法是：马尔可夫链是否有 “稳态”？
也就是说，当链条足够长时，链条上出现的不同状态是否会收敛于某个比例
经过试验统计，比如 100W 长度的链条，发现确实会收敛于某个比例

那么是否可以通过计算得到 “稳态” 呢？是可以的，如下图，分别是转移矩阵 A，和状态概率矢量 pi
通过让状态概率矢量 pi 和转移矩阵A 相乘，我们可以得到披萨状态的未来概率。（披萨状态用 [0 1 0] 表示）
此时，我们可以把 [0.3 0 0.7] 表示为 pi1，随后用 pi1 x A 来计算 pi2
如果存在稳态，用 pi 表示，那么有 pi x A = pi。此时一看，卧槽，这个 pi 不是特征值为 1 的特征向量嘛？
此时还有另外一个条件：pi 的所有元素加起来必须等于 1，因为每一个元素代表一个东西的概率
于是，有两个等式，如下图

于是，有两个等式，如下图，分别是：
1.pi x A = pi
2.pi[1] + pi[2] + pi[3] = 1
解完这两个等式后，我们得到了下图的内容，就是 “稳态”

如下图，是通过两个式子计算出的 “稳态”。
那么，有可能存在多个 “稳态” 嘛？答案是肯定的，我们只需要看一下是否存在不止一个特征值等于1的特征向量即可

---

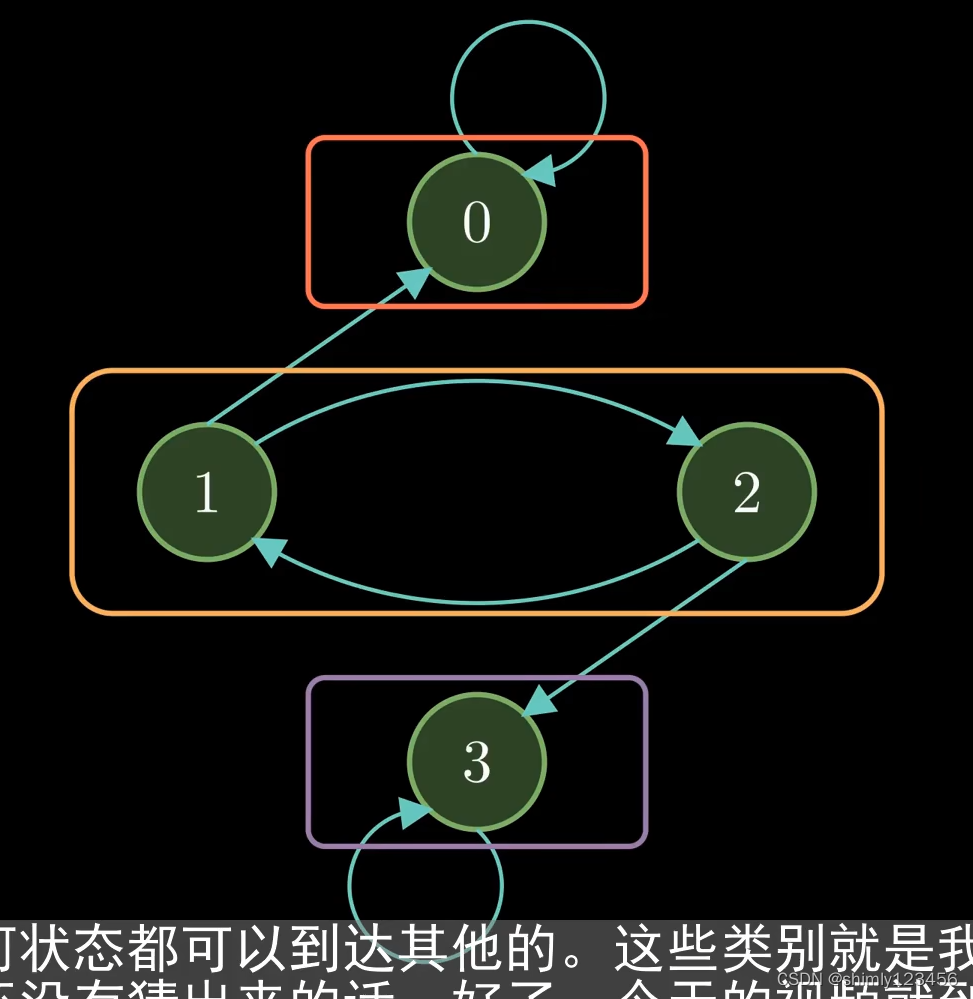
如下图，是一个马尔可夫链。如果状态A到状态B之间有箭头，那么说明从状态A到状态B存在非零的转移概率。
而且明显的，从任何特定状态触发大的转移概率总和一定是1。
需要注意的是：一旦离开状态0，就无法返回了。所以，从状态0出发随机游走，我们无法确定是否会返回状态0
用另一句话来说，从状态0出发，返回状态0的概率小于1
自身返回概率小于1的状态，我们成为 “暂态”
相对的，从状态1触发随机游走，经过一段时间一定能回到状态1，这种状态我们称之为 “常返状态”
状态1和2都是常返状态
这种有些状态无法从其它状态返回的马尔可夫链，我们称之为可约的

如下图，如果每个状态都能从其它状态到达（所有状态都是“常返状态”），我们称为“不可约链”

为什么称呼一些马尔可夫链为 “可约” 呢？原因是它可以被分割成更小的不可约的马尔可夫链

下面是一个经典的可约马尔可夫链，我们称之为 “赌徒的毁灭”
我们可以发现，能双向通信的状态只有 1 和 2
状态1和2可以互相转换，0 和 3 只能自我循环
根据这种通信方式，我们可以把状态分为三个类，分别是 0，1和2，还有3。
在这些类别中，任何状态都可以到达其它的状态，这就是我们所说的通信类

---

根据第一个视频，我们可以知道，每一个马尔可夫链都有一个转移矩阵。
那么，我们可以根据这个转移矩阵，求出所有的 Pij(n)，即，通过 n 步，从状态i 到状态j 的概率

如下图，Pij(1) = Aij

如下图，以计算 P02(2) 为例，它实际上是 转移矩阵A 的 第一行 和 第三列 点乘的结果

A^2 的意义：这个矩阵包含了所有的 Pij(2)，如下图
两步内从 状态i 到 状态j 的概率就等于 A^2 矩阵中 第i行 和 第j列 的元素。

接下来学习一个定理：Chapman-Kolmogoro 定理
下图包含了对于这个定理的证明
Pij(n) = 所有 Pik® x Pkj(n-r) 的和。这里面的意义自己去悟应该比我讲更容易。

如果我们求 A^n (n -> 无穷) 的极限，那么可以得到一个 “稳态”矩阵，这里每一行都是一个 “稳态”矢量
但需要注意的是，只有在满足一定条件下，A的无穷次方才会收敛
其中一个条件：不可约性
另一个条件：周期性（未来视频的主题 TODO:）

---

第四个视频讲解了如何使用马尔科夫链来生成福尔摩斯故事，包括代码

仔细看一下，其实就是 n-gram 语言模型嘛