拓扑排序

有向无环图——DAG （Directed acyclic graph）

定义：

在图论中，如果有一个有向图无法从某个顶点出发经过若干条边回到该点，则这个图是一个有向无环图（DAG图）。
有向无环图未必能转化成树，但是任何有向树均为有向无环图。
DAG图是一类较有向树更一般的特殊的有向图。

应用：

有向无环图是描述一项工程或系统的进行过程的有效工具。除最简单的情况之外，几乎所有的工程（project）都可分为若干个称作活动（activity）的子工程，而这些子工程之间，通常受着一定条件的约束，如其中某些子工程的开始必须在另一些子工程完成之后。

拓扑排序

对DAG图G=（V,E）进行拓扑排序后，结果为该图所有顶点的一个线性队列，满足如果G包含边（u，v），则在该序列中，u就出现在v的前面（如果图是有环的，就不可能存在这样的线性序列）。
一个图的拓扑排序可以看成是图中所有的顶点沿水平线排列而成的一个序列，使得所有的有向边均从左指向右。
在很多应用中，有向无环图用于说明事件发生的先后次序。下面是一个该应用的实例：某人的早晨穿衣的过程。
他必须先穿好某些衣服，才能再穿某些衣服（如先穿袜子后穿鞋），其他的某些衣服则可以按任意次序穿戴（如袜子和裤子）；


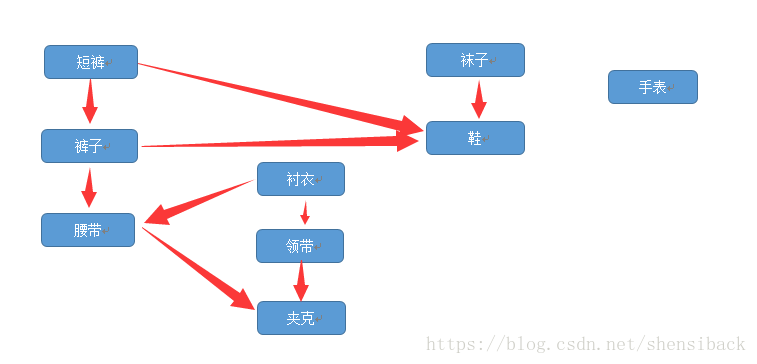
图一：某人对他所穿的衣服进行了拓扑排序。每一条有向边(u,v),都意味着必须先穿衣服u，再穿衣服v。深度优先搜索中的发现和完成时间都在每一个顶点旁边示出。
图二：经过拓扑排序后的同一图形。图中的各个顶点按照完成时间的递降顺序，至左向右排列。注意所有的的有向边都是从左指向右。
图二说明了经拓扑排序的顶点以与其完成时刻相反的顺序出现。
伪代码表示的拓扑排序：

TOPOLOGICAL-SORT(G)
1 call DFS(G) to compute finishing times f[v] for each vertex v
2 as each vertex is finished,insert it onto the front of a linked list
3 return the linked list of vertices

引理：一个有向图G是无回路的，当且仅当对G进行深度优先搜索时没有得到反向边
定理： TOPOLOGICAL-SORT(G)算法产生一个有向无回路图G的拓扑排序。
以上部分内容整理来源于百度和算法导论。