西瓜书 - 支持向量机

间隔与支持向量

给定训练样本集D={(x1,y1),(x2,y2),,,,(xm,ym)},yi∈){−1,+1}D=\{(x_1,y_1),(x_2,y_2),,,,(x_m,y_m)\}, y_i\in)\{-1,+1\}D={(x1​,y1​),(x2​,y2​),,,,(xm​,ym​)},yi​∈){−1,+1},分类学习最基本的想法就是基于训练集D在样本空间中找到一个划分超平面,将不同类别的样本分开.
在样本空间中,划分超平面可通过如下线性方程来描述:
$$w^{T}x+b=0\text{\hspace{1em}(1)}$$
其中$w=(w_1;w_2;...;w_d)$为法向量,决定了超平面的方向;b为位移项,决定了超平面与原点之间的距离.

法向量定义:垂直于平面的直线所表示的向量为该平面的法向量.

证明如下:
设点$x_1,x_2$在超平面中,则有
$$\begin{array}{rl}{w}^T{x}_1+b& =0\\ w^T{x}_2+b& =0\end{array}$$
上面两式相减,有:
$$w_T(x_1-x_2)=0$$
上式标明$w\perp (x_1-x_2)$,差矢量$x_1-x_2$在超平面中,由于$x_1,x_2$是超平面中任意两点,所以w垂直于超平面,即为超平面的法向量.
样本空间中任意点x到超平面(w,b)的距离可写为
$$r=\frac{w^{T}x+b}{||w||}\text{\hspace{1em}(2)}$$
证明:
设p为超平面中任意一点,则点x到超平面的距离为差矢量(x-p)在超平面法向量的投影的绝对值.
$$\begin{array}{rl}r& =|\frac{w^T}{||w^T||}(x-p)|\\ & =\frac{1}{||w^T||}\cdot |w^{T}x-w^{T}p|\\ & =\frac{1}{||w^T||}\cdot |w^{T}x+b|\\ & =\frac{|w^{T}x+b|}{||w||}\end{array}$$
假设超平面(w,b)能将训练样本正确分类,即对于$(x_i,y_i)\in D$,若$y_i=+1$,则有$w^{T}x+b>0$;若$y_i=-1$,则有$w^{T}x+b<0$. 令
$$\begin{array}{rl}{w}^T{x}_i+b& >=+1,y_i=+1\\ w^T{x}_i+b& <=-1,y_i=-1\end{array}\text{\hspace{1em}(3)}$$

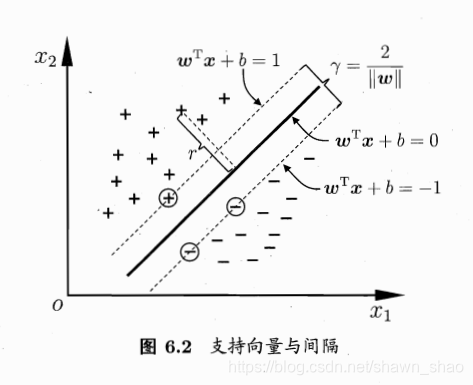
如上图所示,距离超平面最近的几个训练样本使得式(3)的等号成立,它们被称为"支持向量".两个异类支持向量到超平面的距离之和为
$$\gamma =\frac{2}{||w||}\text{\hspace{1em}(4)}$$
它被称为"间隔".
欲找到具有最大间隔的划分超平面,也就是要找到能满足式(3)种约束的参数w和b,使得$\gamma$最大,即
$${}_{w,b}^{max}\frac{2}{||w||}\text{\hspace{1em}(5)}$$
$$y_i(w^T{x}_i+b)>=1$$
显然,为了最大化间隔,仅需最小化||w||.于是,式(5)可重写为
$${}_{w,b}^{min}\frac{1}{2}||w|{|}^2\text{\hspace{1em}(6)}$$
$$y_i(w^T{x}_i+b)>=1$$
这就是支持向量机(Supported Vector Machine)的基本型.

对偶问题

我们希望求解式(6)来得到大间隔划分超平面对应的模型
$$f(x)=w^{T}x+b\text{\hspace{1em}(7)}$$
其中w和b是模型参数.
对式(6)使用拉格朗日乘子法可得到其"对偶问题".具体来说,对式(6)的每条约束添加拉格朗日乘子${\alpha }_i\ge 0$,则该问题的拉格朗日函数可写为
$$L(w,b,\alpha )=\frac{1}{2}||w|{|}^2+\sum _{i=1}^m{\alpha }_i(1-y_i(w^T{x}_i+b))\text{\hspace{1em}(8)}$$
其中$\alpha =({\alpha }_1;{\alpha }_2;...;{\alpha }_m)$.令$L(w,b,\alpha )$对w和b的偏导为零可得:
$$\frac{\partial L}{\partial w}=w-\sum _{i=1}^m{\alpha }_i{y}_i{x}_i=0\text{\hspace{1em}(9)}$$
$$\frac{\partial L}{\partial b}=\sum _{i=1}^m{\alpha }_i{y}_i=0\text{\hspace{1em}(10)}$$
将式(9)(10)带入式(8),有:
$$\begin{array}{rl}L(w,b,\alpha )& =\frac{1}{2}||w|{|}^2+\sum _{i=1}^m{\alpha }_i(1-y_i(w^T{x}_i+b))\\ & =\frac{1}{2}(\sum _{i=1}^m{\alpha }_i{y}_i{x}_i{)}^2+\sum _{i=1}^m{\alpha }_i(1-y_i(\sum _{i=1}^m{\alpha }_i{y}_i{x}_i^T{x}_i+b))\\ & =\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j+\sum _{i=1}^m{\alpha }_i-\sum _{i=1}^m{\alpha }_i{y}_i\sum _{i=1}^m{\alpha }_i{y}_i{x}_i^T{x}_i-\sum _{i=1}^m{\alpha }_i{y}_{i}b\\ & =\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j\end{array}$$
则将问题转换为式(6)的对偶问题:

$${}_{\alpha }^{max}\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j\text{\hspace{1em}(11)}$$
$$s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0,{\alpha }_i\ge 0$$

解出$\alpha$后,求出w和b即可得到模型:
$$f(x)=w^T{x}_{+}b=\sum _{i=1}^m{\alpha }_i{y}_i{x}_i^{T}x+b\text{\hspace{1em}(12)}$$
从对偶问题解除的$\alpha$是式(8)中的拉格朗日乘子,它对应着训练样本$(x_i,y_i)$.注意到式(6)中有不等式约束,因此上述过程需满足KKT要求,即:
$$\{\begin{array}{l}{\alpha }_i\ge 0\\ y_{i}f(x_i)-1\ge 0\\ {\alpha }_i(y_{i}f(x_i)-1)=0\end{array}\text{\hspace{1em}(13)}$$
于是,对任意训练样本$(x_i,y_i)$,总有${\alpha }_i=0$或$y_{i}f(x_i)=1$.
若${\alpha }_i=0$,则该样本不会在式(12)的求和中出现,也就不会对f(x)有任何影响;若${\alpha }_i>0$,则必有$y_{i}f(x_i)=1$,所对应的样本点位于最大间隔边界上.
这显示出支持向量机的一个重要性质:训练完成后,大部分的训练样本都不需保留,最终模型仅与支持向量有关.

SMO算法

如果求解式(11), SMO(Sequential Minimal Optimization)是其中一个著名高效算法.
SMO的基本思路是先固定${\alpha }_i$之外的所有参数,然后求${\alpha }_i$上的极值.由于存在约束${\sum }_{i=1}^m{\alpha }_i{y}_i=0$,若固定${\alpha }_i$之外的其它变量,则${\alpha }_i$可由其它变量导出.
于是,SMO每次选择两个变量${\alpha }_i$和${\alpha }_j$,并固定其它参数.这样,在参数初始化后,SMO不断执行如下两个步骤直至收敛:

• 选取一对需更新的变量${\alpha }_i$和${\alpha }_j$
• 固定${\alpha }_i$和${\alpha }_j$以外的参数,求解式(11)获得更新后的${\alpha }_i$和${\alpha }_j$

SMO算法之所以高效,恰由于在固定其它参数后,仅优化两个参数的过程能做到非常高效.具体来说,仅考虑${\alpha }_i$和${\alpha }_j$时,式(11)的约束可重写为
$${\alpha }_i+{\alpha }_j=c,{\alpha }_i\ge 0,{\alpha }_j\ge 0\text{\hspace{1em}(14)}$$
其中
$$c=-\sum _{k\ne i,j}{\alpha }_k{y}_k\text{\hspace{1em}(15)}$$
是使${\sum }_{i=1}^m{\alpha }_i{y}_i=0$成立的常数.用式(14)消除式子(11)中的变量${\alpha }_j$,则得到一个关于${\alpha }_i$的单变量二次规划问题,仅有的约束是${\alpha }_i\ge 0$.可高效的计算出更新后的${\alpha }_i$和${\alpha }_j$.
**如何确定偏移项b?**注意到对任意支持向量$(x_s,y_s)$都有$y_{s}f(x_s)=1$,即:
$$y_s(\sum _{i\in S}{\alpha }_i{y}_i{x}_i^T{x}_s+b)=1$$
其中S为所有支持向量的下标集.b的求解通常使用所有支持向量求解的平均值:
$$b=\frac{1}{|S|}\sum _{s\in S}(\frac{1}{y_s}-\sum _{i\in S}{\alpha }_i{y}_i{x}_i^T{x}_s)$$

核函数

在前面的讨论中,我们假设样本是线性可分的,即存在一个划分超平面能将训练样本正确分类.然而在现实任务中,原始样本空间内也许并不存在一个能正确划分两类样本的超平面.
对于这样的问题,可将样本从原始空间映射到一个更高维的特征空间,是的样本在这个特征空间内线性可分.
令$\varphi (x)$表示将x映射后的特征向量,于是,在特征空间中划分超平面所对应的模型可表示为
$$f(x)=w^T\varphi (x)+b\text{\hspace{1em}(19)}$$
其中w和b是模型参数,类似于式(6),有:
$${}_{w,b}^{min}\frac{1}{2}||w|{|}^2\text{\hspace{1em}(20)}$$
$$y_i(w^T\varphi (x_i)+b)>=1$$
其对偶问题是:

$${}_{\alpha }^{max}\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j\varphi (x_i{)}^T\varphi (x_j)\text{\hspace{1em}(21)}$$
$$s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0,{\alpha }_i\ge 0$$

求解式(21)涉及到计算$\varphi (x_i{)}^T\varphi (x_j)$,这是样本$x_i$与$x_j$映射到特征空间之后的内积.由于特征空间维数可能很高,甚至可能是无穷维,因此直接计算$\varphi (x_i{)}^T\varphi (x_j)$通常是苦难的.为了避开这个障碍,可以设想这样一个函数:
$$\beta (x_i,x_j)=<\varphi (x_i),\varphi (x_j)>=\varphi (x_i{)}^T\varphi (x_j)\text{\hspace{1em}(22)}$$
即$x_i$与$x_j$在特征空间的内积等于它们在原始样本空间通过函数$\beta (.,.)$计算的结果.有了这样的函数,我们就不必直接去计算高维甚至无穷维特征空间中的内积,于是式(21)可重写为:

$${}_{\alpha }^{max}\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j\beta (x_i,x_j)\text{\hspace{1em}(23)}$$
$$s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0,{\alpha }_i\ge 0$$

求解后即可得到:

$$\begin{array}{rl}f(x)& =w^T\varphi (x)+b\\ & =\sum _{i=1}^m{\alpha }_i{y}_i\varphi (x_i{)}^T\varphi (x)+b\\ & =\sum _{i=1}^m{\alpha }_i{y}_i\beta (x,x_i)+b\end{array}\text{\hspace{1em}(24)}$$

这里的函数$\beta (.,.)$就是"核函数".