洛谷P1291 SHOI2002 期望

传送门:题目

题意：

每瓶可乐都印有一个人的名字，一共有n个不同的名字，出现的概率都相等，问期望买几瓶可能能集齐所有的名字。

题解：

典型的期望题。
我们不能分别考虑每一个人名出现的概率。因为考虑单独的一个人名的时候所买的“没用”的饮料在考虑其他人名的时候可能会变成有用的。所以我们需要整体考虑：
我们当前已经集齐了$k$个球星的名字，我们想知道集齐$k+1$个球星名字的概率是多少，不难想到，目前状态下：$k个是没用的(n-k)是有用的$，那么$P(A)=\frac{n-k}{n}$，则期望天数$=\frac{n}{n-k}$，$k \in [0,n-1]$。
那么$Ans=\sum_{k=0}^{n-1}\frac{n}{n-k}$
化简一下：

$Ans=n*\sum_{k=1}^{n} \frac{1}{k}$

坑点：

洛谷这道题把输出格式改了一下，和原来的SHOI2002输出格式不一样。
洛谷要求输出格式如下：
我们以lena代表整数部分长度，lenb代表分母部分长度；
洛谷要求先输出lena长度的空格，再输出分子，再输出换行，再输出整数，再输出lenb的’-‘代表分数线，再输出换行，再输出lena长度的空格，在输出分母，再输出空格。
是不是很乱，我举个栗子：

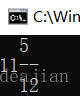
Input:5
Output:

AC代码：

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <sstream>
#define debug(x) cout<<#x<<" = "<<x<<endl;
#define INF 0x3f3f3f3f
#define int long long
using namespace std;

long long a = 1, b = 1;//a is numerator b is denominator
void Harmonic_series(int n) {
    for (int i = 2; i <= n; i++)  {
        a = a * i + b;
        b = b * i;
        int temp = __gcd(a, b);
        a /= temp;
        b /= temp;
    }
}

signed main(void){
    int n;
    cin>>n;    
    Harmonic_series(n);
    a*=n;
    if(a%b==0)
        cout<<a/b<<endl;
    else{
        int temp;
        temp=__gcd(a,b);
        a/=temp;
        b/=temp;
        stringstream ss;//转成字符串计算数字长度
        ss<<a/b;
        string str,str2;
        ss>>str;
        for(int i=0;i<str.size();i++)
            str[i]=' ';
        ss.clear();//多次使用ss记得clear（）
        ss<<b;
        ss>>str2;
        for(int i=0;i<str2.size();i++)
            str2[i]='-';
        cout<<str<<a%b<<endl<<a/b<<str2<<endl<<str<<b<<endl;
    }
    return 0;
}