UVAlive 3716 表达式 画图

思维题，我们先求出表达式，我们记sum[i]表示从[1-i]中不同的字母的总数，那么，区间[l,r]就可以转化为

(sum[j]-sum[i-1]) / (j-i) <= p/100

为了方便，我们把i-1计为i，然后化简上式，得到：

100*sum[j]-p*j<=100*sum[i]-p*i

我们可以分析，自变量j>i，因变量f(j)<f(i)，所以我们可以创建一个结构体，记录两个值，一个是它的index，另一个是f()，然后把f()按升序sort一遍，求出它的index最长"连续"降序长度，不连续也没事，只要保障入点是极大值。

不明白没有关系，我们可以画图。

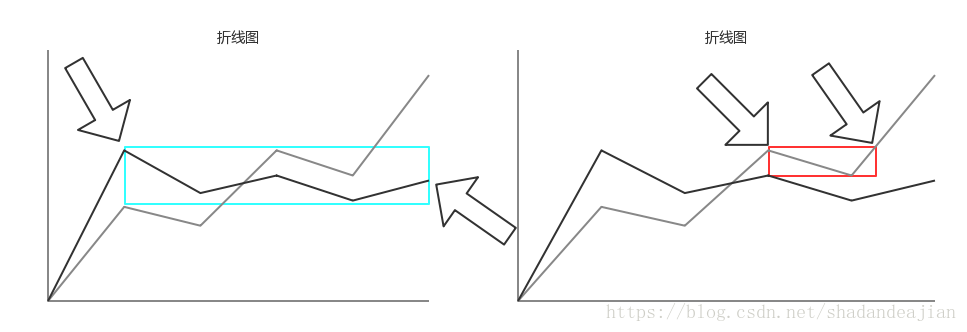
 先看第一幅图，只看蓝色方框内的粗体线，我们假定这个区域就是[l,r]，l就是最左边的入点，r就是最右边的出点，我们看到，入点等于极大点，所以这段区间可取。

再看第二幅图，只看红色方框内的浅体线，我们假定这个区域就是[l,r]，l就是最左边的入点，r就是最右边的出点，我们看到，入点等于极大点，所以这段区间可取，但是只要红色方框的右边界再往右走一点，那么出点就是极大值了，就变成不可取的状态了。

#include<iostream>
#include<algorithm>
using namespace std;
struct Node {
    int sum,id;
    bool operator<(const Node& rhs)const {
        if(sum==rhs.sum)
            return id>rhs.id;
        return sum<rhs.sum;
    }
} node[150000+10];
int main(void) {
    int n,p;
    string s1,s2;
    while(cin>>n>>p&&n+p) {
        cin>>s1>>s2;
        node[0].sum=0,node[0].id=0;
        for(int i=0; i<n; i++) {
            if(s1[i]!=s2[i])
                node[i+1].sum=node[i].sum+1;
            else
                node[i+1].sum=node[i].sum;
        }
        for(int i=1; i<=n; i++) {
            node[i].sum=node[i].sum*100-p*i;
            node[i].id=i;
        }
        sort(node,node+n+1);
        int ans=0,temp=n+10;
        for(int i=n; i>=0; i--) {
            if(node[i].id>temp)
                ans=max(ans,node[i].id-temp);
            else
                temp=min(temp,node[i].id);
        }
        if(ans==0)
            cout<<"No solution."<<"\n";
        else
            cout<<ans<<"\n";
    }
    return 0;
}