Manaher算法

                                                 Manacher算法

Manacher算法能够在O（N）的时间复杂度内得到一个字符串以任意位置为中心的回文字符串。算法的基本原理是：利用已知的左半部分去推右半部分。

 

令rad[i] 表示：第i个字符的回文半径，即rad[i]尽可能大。且满足s[i – rad[i] ,i-1] = s[i+1, i+rad[i] ]。

假设回文字符串长度为奇数的情况：

 

（1）rad[i - k] < rad[i] - k

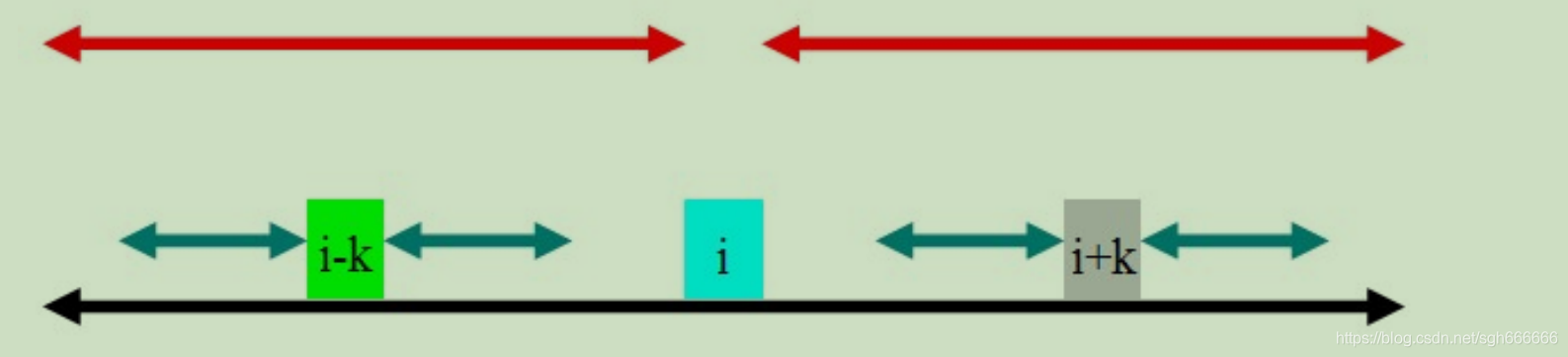
红色部分代表 rad[i]， i点到两边的点距离均为k。

很显然这时候rad[i + k] = rad[i - k];

 

 

(2) rad[i-k] > rad[i] - k

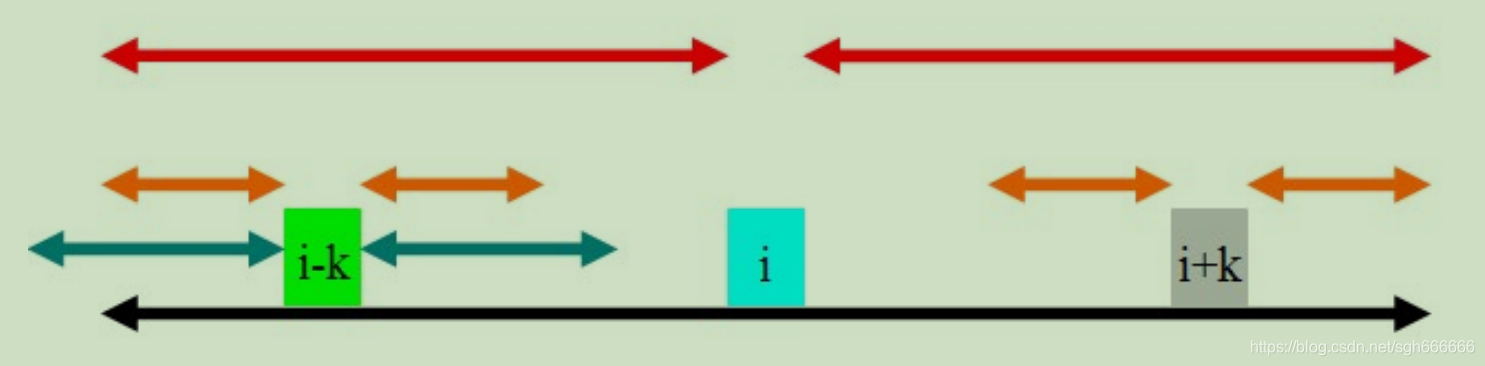
这时候rad[i + k] = rad[i ]-k 成立，因为rad[i + k]不可能再大了，否则rad[i]也要跟着大。

 

综上，当rad[i-k] != rad[i]-k的时候，rad[i + k] = min(rad[i-k], rad[i]-k);

（3）rad[i - k]  == rad[i] - k

 

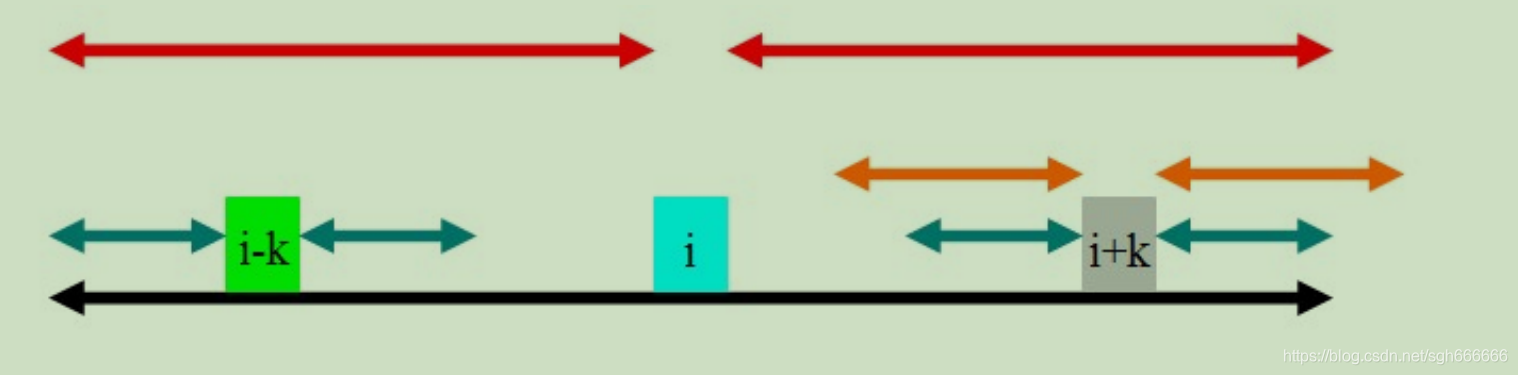
此时不能根据i去直接推算出i+k的具体回文，需要调到i+k位置，同时把i的半径-k作为i+k的起始回文长度，开始扫描i+k位置的回文长度。

 

 

但是，偶数情况怎么办？

构造出奇数情况就可以了。比如:aabbaca，把它变成  (#a#a#b#b#a#c#a#) ，括号是为了防止越界。这样位置i在原始字符串位置为(i - 1) / 2。  当前中间为 # 时，就是偶数情况，比如abba中间为坐标为7的#，aca的中间就是c。

 

 

来看几道例题：

HDU---3068 ： 求字符串最长回文长度。

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,n) for (int i=a;i<n;i++)
#define per(i,a,n) for (int i=n-1;i>=a;i--)
#define oo cout<<"!!!"<<endl;
typedef long long ll;
typedef unsigned long long ull;
#define ms(s) memset(s, 0, sizeof(s))
const int inf = 0x3f3f3f3f;
const int mod = 1e9+7;
//head

const int maxn = 1e6+11;

char str[maxn],cpy[maxn];
int rad[maxn];

void manacher(char s[],int length,int rad[])	
{
	for(int i = 1,j=0,k; i < length;i+=k,j-=k)
	{
		while(s[i-j-1] == s[i+j+1])j++;
		rad[i] = j;
		for(k = 1;k<rad[i] && rad[i-k]!=rad[i]-k;k++)
			rad[i+k] = min(rad[i-k],rad[i]-k);
		
	}

}

int main() 
{
	while(scanf("%s",str)!=EOF)
	{
		int len = strlen(str);
		cpy[0] = '(',cpy[1] = '#';
		for(int i = 0,j = 2;i<len;i++,j+=2)
		{
			cpy[j] = str[i];
			cpy[j+1] = '#';
		}
		len = len*2 + 3;
		cpy[len-1] = ')';
		manacher(cpy,len,rad);
		int _max = 1;
		rep(i,0,len)
		{
			_max = max(_max,rad[i]);
		}
		cout << _max << endl;
	}
    return 0;
}

 

 

 

5. 最长回文子串

class Solution {
public:
    string longestPalindrome(string s) {
  		string ss = "(#";
  		for(int i = 0;i<s.size();i++){
  			ss += s[i];
  			ss += '#';
  		}
  		ss+=')';
  		// cout << ss << endl;
  		// cout << s << endl;
  		vector<int> rad(ss.size(),0);
  		int maxi = -1;
  		int maxlen = -1;
  		for(int i = 1,j = 0,k; i < ss.size(); i+=k,j-=k)
  		{
  			while(ss[i-j-1] == ss[i+j+1])j++;
  			rad[i] = j;A
  			if(rad[i] > maxlen){
  				maxlen = rad[i];
  				maxi = i;
  			}
  			for(k = 1;k<rad[i] && rad[i-k]!=rad[i]-k;k++)
  				rad[i+k] = min(rad[i-k],rad[i]-k);
  		}
        cout << maxi << endl;
  		cout << maxlen << endl;
  		return s.substr((maxi-1)/2 - maxlen/2,maxlen);

    }
};

 

 

ZOJ---4110 ： 浙大19校赛，分析可得manacher基本运用。

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<string>
#include<string>
#include<vector>
#include<queue>
#include<stack>
#include<cmath>
#include<set>
#include<map>
using namespace std;
#define rep(i,a,n) for (int i=a;i<n;i++)
#define per(i,a,n) for (int i=n-1;i>=a;i--)
#define oo cout<<"!!!"<<endl;
typedef long long ll;
typedef unsigned long long ull;
#define ms(s) memset(s, 0, sizeof(s))
const int inf = 0x3f3f3f3f;
//head

const int maxn = 4e6+11;
char s[maxn],cpy[maxn],a[maxn],b[maxn];
int rad[maxn];

ll manacher(){
	ll res = 0;
	int len  = strlen(cpy);
	for(int i = 1,j = 0,k;i<len;i+=k,j-=k){
		while(cpy[i-j-1] == cpy[i+j+1])j++;
		rad[i] = j;
		res += (rad[i]+1)/2;
		for(k = 1;k<rad[i] && rad[i-k] != rad[i] - k;++k){
			rad[i+k] = min(rad[i-k],rad[i] - k);
			res += (rad[i+k]+1)/2;
		}
	}
	return res;
}
int main() 
{      
	int T;cin>>T;
	while(T--){
		scanf("%s %s",a,b);
		strcpy(s,a);

		int n = strlen(s);
		cpy[0] = '(';
		cpy[1] = '#';

		for(int i = 0,j = 2;i<n;++i,j+=2){
			cpy[j] = s[i];
			cpy[j+1] = '#';
		}
		int len = 2*n+3;
		cpy[len] = 0;
		cpy[len-1] = ')';
		int l = 0,r = n-1;
		while(l<n){
			if(a[l] != b[l]){
				break;
			}
			++l;
		}

		while(r>=0){
			if(a[r] != b[r]){
				break;
			}
			--r;
		}

		if(l == r)puts("0");
		else if(l<n){
			int ans = 1;
			if(l<n){
				for(int i = l;i<=r;++i){
					if(a[i] != b[r-i+l]){
						ans = 0;break;
					}
				}
			}
			if(ans){
				--l,++r;
				while(l>=0 && r < n && a[l] == b[r] && a[r] == b[l]){
					ans++,--l,++r;
				}
			}
			cout << ans << endl;


		}
		else cout << manacher()<<endl;
    
	}
}

 

 

HDU---4513: 最长单调回文字符串

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,n) for (int i=a;i<n;i++)
#define per(i,a,n) for (int i=n-1;i>=a;i--)
#define oo cout<<"!!!"<<endl;
typedef long long ll;
typedef unsigned long long ull;
#define ms(s) memset(s, 0, sizeof(s))
const int inf = 0x3f3f3f3f;
const int mod = 1e9+7;
//head

const int maxn = 1e6+11;

int n;
int seq[maxn];
int rad[maxn];

inline bool check(int seq[],int a,int b)
{
	if(seq[a] != seq[b])return false;
	if(!seq[a] || a == b)return true;
	int ar = a+2;
	if(seq[a] <= seq[ar])return true;
	return false;
}

void manacher(int sq[],int rad[],int length)
{
	for(int i=1,j=0,k;i<length;i+=k,j-=k)
	{
		while(check(seq,i-j-1,i+j+1))j++;
		rad[i] = j;
		for(k = 1;k<=j &&rad[i-k]!=rad[i]-k;k++)
			rad[i+k] = min(rad[i-k],rad[i]-k);
	}
}

int main() 
{
	int T;
	cin>>T;
	while(T--)
	{
		ms(seq);
		cin >> n;
		seq[0] = inf-1;
		for(int i = 2,j=0;j<n;i+=2,j++)
		{
			scanf("%d",seq+i);
		}

		n = 2*n+3;
		seq[n-1] = inf-2;
		manacher(seq,rad,n);
		int res = 1;
		for(int i = 0;i<n;i++)
			res = max(res,rad[i]);
		cout << res << endl; 
	}
    return 0;
}

 

 

LeetCode647. 回文子串

给定一个字符串，你的任务是计算这个字符串中有多少个回文子串。

具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被计为是不同的子串。

示例 1:

输入: "abc"
输出: 3
解释: 三个回文子串: "a", "b", "c".
示例 2:

输入: "aaa"
输出: 6
说明: 6个回文子串: "a", "a", "a", "aa", "aa", "aaa"

题解:和浙大校赛题差不多,求回文子串数.

class Solution {
public:
    char cpy[2222];
    int rad[2222];
    int manacher()
    {
	    int res = 0;
	    int len  = strlen(cpy);
	    for(int i = 1,j = 0,k;i<len;i+=k,j-=k){
		    while(cpy[i-j-1] == cpy[i+j+1])j++;
		    rad[i] = j;
		    res += (rad[i]+1)/2;
		    for(k = 1;k<rad[i] && rad[i-k] != rad[i] - k;++k){
		    	rad[i+k] = min(rad[i-k],rad[i] - k);
			    res += (rad[i+k]+1)/2;
		    }
	}
	return res;
    }
    
    int countSubstrings(string s) {
        int n = s.size();
        cpy[0] = '(';
		cpy[1] = '#';
 
		for(int i = 0,j = 2;i<n;++i,j+=2){
			cpy[j] = s[i];
			cpy[j+1] = '#';
		}
		int len = 2*n+3;
		cpy[len] = 0;
		cpy[len-1] = ')';
        return manacher();
    }
};