贪心算法题总结

选择当前最优的策略 希望得到全局最优

尽量把10找出去 因为两个5可以凑10

应该是要默认一定是可以把数组缩减为一半

所以我们每次都选最大的肯定最快

用lamda表达式定义新的排序

先把nums1排序 再把nums2的索引按照nums2索引的元素的大小排序

然后遍历nums1

令nums2排序后的索引数组index 左指针left 右指针right

对应的原数比较 nums1当前元素x大于index[left]索引的数则 位置就index[left] 若小于则把x放到index[right]的位置

有动态规划的做法 

贪心的做法是 定义一个ret数组 从左到右遍历nums

如果当前数x比ret的末尾要大 就尾插

如果不是 那么用x替换ret中第一个大于x的数

这一步很关键 因为替换是为了测试后面有没有更优的序列 

如果有 那根据这个方法 x后面的数也会慢慢被换掉

如果没有 那也不影响后续的尾插

贪心 碰到I就插入当前最小的数 碰到D就插当前最大的数

和优势洗牌差不多而且更简单 此题不需要映射 直接双指针 固定孩子 让另一个指针去找饼干 找不到 孩子指针就不++

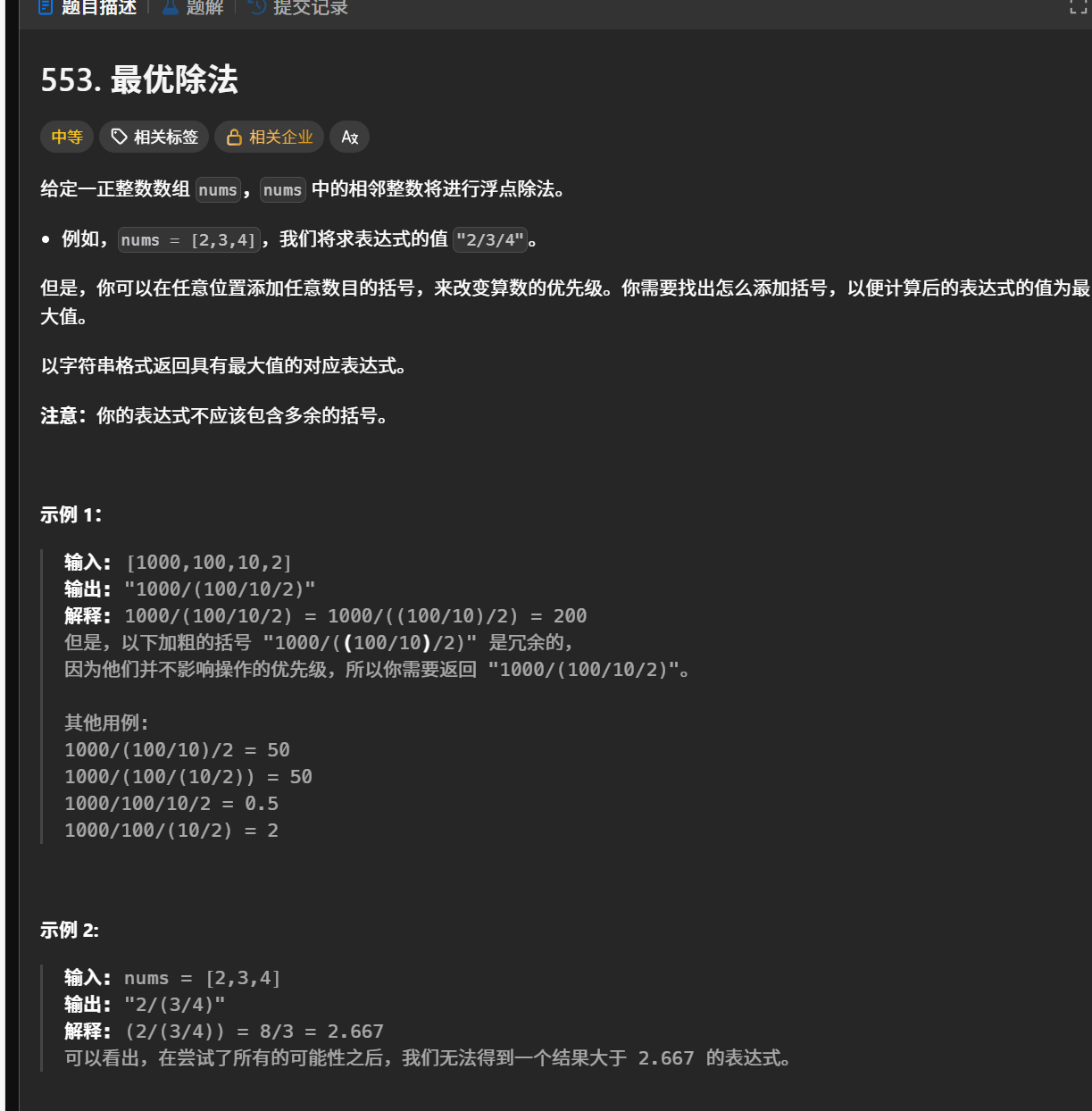除了第二个数其他都放在分子上就行了

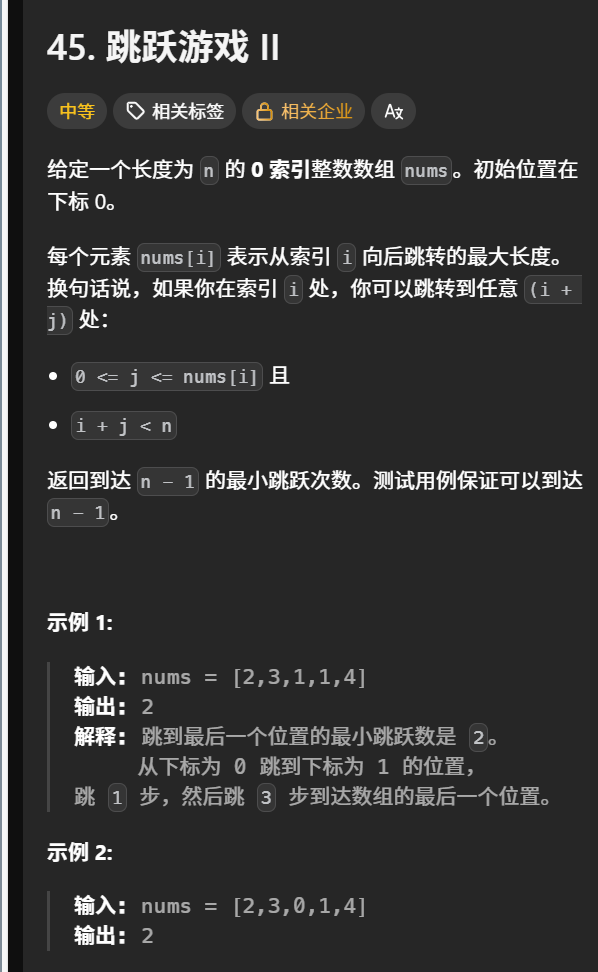
动态规划可以给出一个on2的做法 dp[i]=dp[k]+1 if(k+nums[k]>i)

贪心做法是层序遍历 一个left 一个right 一个max_pos

left负责遍历当前层 max_pos代表当前层最多能到达的位置

遍历到right时 把left更新成right+1 right更新成max_pos即上一层所能到达的最高位置

定义净收入数组diff

计算净收益 当净收益为负 则在当前下标的后一个开始遍历

贪心点在于每次多移动一些距离

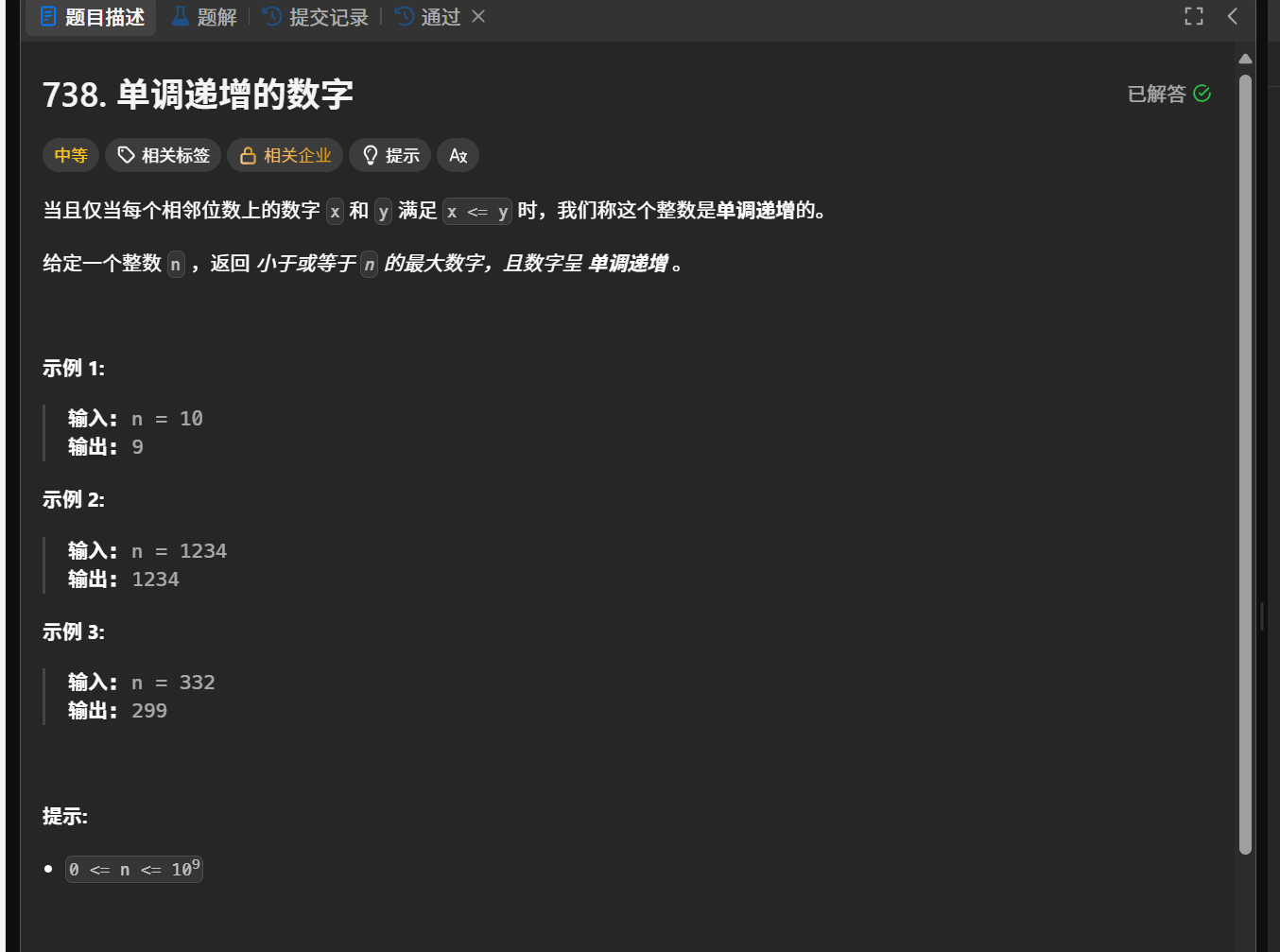
先把数字转化为字符串 然后遍历找到第一个不满足递增的数字 把它前面的一个数字减一 再把后面的数字全部置成9

这题只能反向操作 正向操作 让start去变大 那么减法也要减得更多

于是我们让target先变小 再加1 此时变小已经缩小减法需要的步数

区间问题在贪心中非常经典 一般要先排序

然后定义左右指针 标记当前不重叠区间

找到重叠的就更新right

找到不重叠的就更新left 

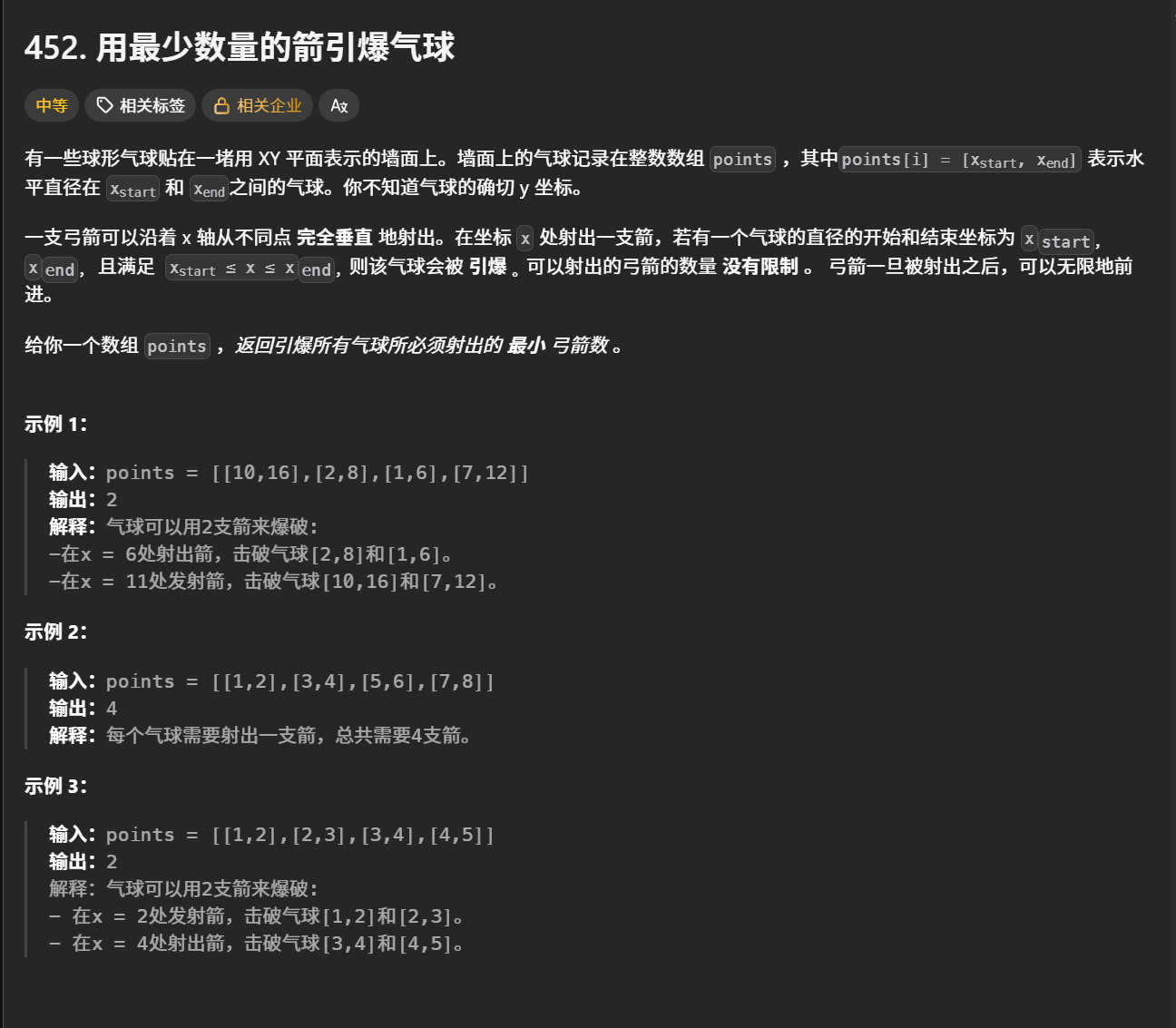
本质上也是区间问题

一有重叠的就求并集 看看有多少个并集就可以

非常巧妙 这题看似二维其实 重写排序可退化成一维 

题目要求宽与高严格大于 意思是说 如果有宽相同的 那么顶多只有一个被选入

所以我们重写排序方法 先按宽排序 是为了满足题意