没时间了,只掌握技巧
主要根据作业2-7章
根据现有资料,推断题型为计算题70分,问答题30分,文章最后有一套真题和往年问答题
答案都是参考这位大哥的:https://blog.youkuaiyun.com/capture3333/article/details/127344613.。我只是针对作业学习技巧,认真的大哥块绕道。
第二章 高级语言及其语法描述

①

没啥说的,语言就是推出能用终结符组成的一个集合表示。
②

最左推导就是每次只进行一位最左边的非终结符推导,最右推导就是先推导最右边的终结符,不过得先全局把握一下。
0127的最左推导,很明显我们得先有四个D,然后从左到右一个一个替换为非终结符数字。
0127的最右推导,很明显不断的扩展ND,D得先转换成数字,才能转换N,所以从数字7开始,不断往左展开就好了。

①

和上面一样,先把握一下。
i+ii的最左推导,有加有乘,那就先考虑有加法的E->E+T,然后把E先转成i,后把T转成有乘法的T->TF,反正转就完事。其他的不多说。
②

语法树的画法比推导更直观,也很简单,推出的叶子节点满足要求的表达式就行。这个我们可以根据最左推导来画树。

二义性就是说给你一个文法,存在一个句子,通过最左推导或最右推导来构建树时,有两种或两种以上的推导方法,就是二义的。
这个自己画一画,利用三个候选式,慢慢斟酌。我这里是发现了iiiei这个句子有二义性

第三章 词法分析

这种证明题很繁琐,估计老师认为我们很菜也不会出,保险贴上大哥的链接https://blog.youkuaiyun.com/capture3333/article/details/128062964

构造DFA的步骤如下:
①构造他的NFA:

怎么构造呢,首先对于开始标志我们用X表示,就结束我们用同心圆加Y。同时掌握一下三个规则:

这些i,j是我们构造NFA所添加的状态,反正每替换一部分正则式添一个状态,同时把输入的字符放在箭头上。
②采用子集法画成DNF


啥意思呢,就是先写出所有的I,他的下标对应你有哪些字符,这个正规式只有0和1,所以我们有I0,I1。第一个I表示初态,用来进行构建这个表的。
首先第一步就是|的初态,找出从X出发,箭头上有ε的,箭头指向的状态加入这个集合。很明显,这里X只有输入1的箭头。所以我们只将X加入集合。
然后就是I0,他表示在I的基础上加上0这个字符会通往哪里,很遗憾,哪也去不了,所以为空集。
接着看I1,表示输入1通往哪里,很明显,可以通到状态1,所以我们把状态1加入集合,同时,对于输入字符为ε的我们也要加入集合,这里1通2,2通3。所以2,3加入集合。
走完了一行,我们更新初态,为了方便,按出现次序将集合标号,最终初态也是包括所有状态。对于初态为ε,我们省略。
第二行从标号2开始,按照第一行的套路,写完整个表。
总结:
1:将X加入初态,并将输入为ε能到达的的状态加入集合
2:将每种字符都当作输入,将能到达的状态或者后面有输入ε能到达的状态加入集合
3:为每个集合编号,并且第一列的每一行按照编号顺序执行建表
4:根据表来画DNF,很简单,包括Y的集合我们最终设置为结束状态,同时最后可以去除集合为ε的点。
③化简DNF

1:将状态按终止状态划分成两个集合
非终止态:{0,1,2,3,4},终止态:{5}
2:细分非终止态和终止态
很明显终止态只有一个状态不可分了。只看非终止态。
一个集合是否可以划分,需要求出该集合通过输入正规式出现的字符所能到达状态的集合是否在已有的某个集合里(或者是子集)。同时,只有部分输入字符单独划分。
这里{0,1,2,3,4}输入0可到达的状态为{2,4},{2,4}属于集合{0,1,2,3,4},输入1可到达的状态为{1,3,5},不属于任何集合,则继续划分。
观察到状态0只有输入1,则单独划分,只有状态4通往5,也单独划分,这样就有{0},{1,2,3},{4},{5}。
对{1,2,3}输入0,得到{2,4},输入1得到{3},由于4之前分出去了,{2,4}不属于任何一个集合,则{1,2,3}继续划分。
观察到只有3输入字符0进入4,所以单独划分3,此时有{0},{1,2},{3},{4},{5}。
对{1,2}输入0,得到{2},输入1得到{3}。两个集合都能找到,则不需要继续划分。
将{1,2}合并即可得到化简的DBF.

①
(1|0)*01
②
(1|2|3|4|5|6|7|8|9)(0|1|2|3|4|5|6|7|8|9)*(0|5)
动脑经就可以想到

给出正规式:(0|1)*010(0|1) *
然后和上面那题一样,先构建NFA…

确定化和最小化对于化成DNF,以及DNF的化简。
箭头指向为开始位置。



这里化简仔细看一看,再对比之前那题步骤,已做修改

写出正规式(0|10)*就没问题,其他步骤根据之前的


第四章 语法分析-自上而下分析

贴上大哥的链接:https://blog.youkuaiyun.com/capture3333/article/details/129557142
程序估计老师认为我们蠢不会出。
消除左递归且看下面的方法

①观察文法,第二个推导式很明显符合左递归,对着上面图片抄就行:
S->a|^|(T)
T->ST’
T’->,ST’|ε
②
什么是LL(1)文法:

看不懂没关系,我们先掌握技巧。

首先我们得求出所有非终结符的First集合和Follow集合:
First集合求法:推导式左边是非终结符,我们去候选式中看,如果第一个字符为终结符,那就添加到该集合。如果第一个不是终结符,那么这个First集合等于这个非终结符的First集合去除ε,看起来像一个递归过程,话不多说,上技巧。
第一个非终结符是S,候选式有三个终结符,都给添加到First(S)中,此时First(S)={a,^,(},第二个非终结符First(T),候选式第一个字符为非终结符,则First(T) = First(S) = {a, ^,(}。第三个非终结符First(T‘)={,ε}。
Follow集合求法:我们首先将#加入到开始符的Follow集中。假设我们找L的Follow集,我们首先去推导式右边找到L,接着有以下规则:
1:如果L的右边是终结符,那么终结符加入该集合
2:如果L的右边是非终结符,那么把右边这个非终结符的First集合去除ε加入该集合,并且将该推导式子->左边的Follow集加入该集合(如果没有First集合没有ε就不要加)
3:如果L在末尾,将推导式子->左边的Follow集加入该集合
将#加入Follow(s)中
对于Follow(S),第二三个推导式有右边都有,且后面都为T’,所以根据规则2,Follow(S)=First(T’)+Follow(T)+Follow(T’)。但是后面两个暂时为空,Follow(S)={#,,}。Follow(T)={)}。Follow(T’)=Follow(T)={)}。这时后面两个Follow不在变化,而最开始的Follow(S)需要加上Follow(T)和Follow(T’),即Follow(S)={#,,,)}
判断是否为LL(1)文法:
1:文法不含左递归
2:候选首符集就是用|隔开的首选式,将每个候选集的First集都进行交运算,结果为空,则第二个条件成立
3:将候选集包含ε对应的非终结符的First集合与Follow集合进行交运算,如果结果为空,则属于LL(1)文法。
这里第三问First(T’)∩Follow(T’)=空,和大哥写的不一样。
构建预测分析表:
1:当非终结符遇到其First集中的终结符填入相应候选式
2:当非终结符First集中含有ε元素时,遇到其Follow集中的终结符时填入非终结符->ε

看大哥的答案

看大哥的答案

看大哥答案
第五章 语法分析-自下而上分析
大哥链接

证明句型和之前的最左(右)推导差不多,这里用语法树表示

短语:就是把每个非叶子节点当作根节点,该树的叶子节点组合为一个短语。这里先将E作为根节点,叶子节点就有E+T* F,接着将T作为根节点,此时叶子节点有T* F。
直接短语:子数只有两代的短语就是直接短语,这里就是T*F。
句柄:最左边的直接短语就是据句柄。

①最左、最右推导没啥说的之前有。
②写出规范规约,其实就是你的最左最右推导过程从下往上写,可以慢慢构建语法树,看句柄,规约规则就是对于文法推导。

移进-规约步骤

 移进-规约步骤就是根据我们的规范规约,设置一个分析栈,属于的字符串开头结尾都添加#,接着不断移进,并观察分析栈是否有句柄出现,一出现就进行规约操作,并且这个规约操作对应规范规约的一行行进行。规范规约有17个,对应我们规约17次。
移进-规约步骤就是根据我们的规范规约,设置一个分析栈,属于的字符串开头结尾都添加#,接着不断移进,并观察分析栈是否有句柄出现,一出现就进行规约操作,并且这个规约操作对应规范规约的一行行进行。规范规约有17个,对应我们规约17次。
语法树构建过程也是看规范规约,一行一行的化,看下面的图好好琢磨。
更清晰的步骤:


练习二的题目:


①
构建FIRSTVT的规则如下:
1:如果某非终结符的候选式的第一个或第一个为非终结符第二个字符为终结符,则该终结符加入该集合
2:如果非终结符的候选式的第一个为非终结符,将第一个非终结符的FIRSTVT集合加入该集合。
这个题目FIRSTVT(S)的右边有三个第一个为终结符的,所以为{a,^,(}.FIRSTVT(T)有第二个字符终结符的,并且有两个非终结符开头的,但是第一个和左边的相同都为T,所以只需要加上FIRSTVT(S),
FIRSTVT(T)={, ,a,^,(}
构建LASTVT的规则如下:和上面差不多,last就是后面的嘛
1:如果某非终结符的候选式的倒数第一个或倒数第一个为非终结符倒数第二个字符为终结符,则该终结符加入该集合
2:如果非终结符的候选式的倒数第一个为非终结符,将倒数第一个终结符的FIRSTVT集合加入该集合。
同理不多说
②
啥是算符优先文法:看不懂没关系,掌握技巧,注意优先级里面有个点
算符文法要满足没有两个挨着的非终结符


对于优先集规则我们转成易理解的(可能不叫大于小于等于不管他,带个点的运算符):
等于:当候选式同时出现两个终结符,他们挨在一起或者隔着一个非终结符,则这两个终结符相等
小于:
当候选式有一个终结符的右边紧挨着非终结符时,该终结符小于该非终结符的FIRSTVT集合的每个元素。
大于:
当候选式有一个终结符的左边紧挨着非终结符时,该非终结符的LASTVT集合的每个元素都比右边的终结符大
总结就是说终结符同时出现相等,出现在左边看LASTVT,出现在右边看FIRSTVT,并且LASTVT和FIRSTVT中的元素都比当前终结符大
这题首先看(T),两个终结符夹着非终结符,则有(=),其次T的FIRSTVT集中所有终结符大于(,LASTVT集中所有终结符大于)。接下来的都类似
画表很简单。

这道题建议不看,直接看我写真题的答案,这大哥写的有问题
①啥是LR(0)项目,建议看看这位大哥的博客
好,看完后,第一题就简单了,首先用增广文法,就是添加一个S’->S,然后一个一个加点就行了

②项目集规范族啥的看麻了,感觉每个人说的不一样,原来是有三种不同求法,这里按照答案给出的闭包求法,也挺简单的
首先构造NFA,构造规则如下



NFA构建规则:
1:如果某个项目a的点往右移动一位到达项目b,则NFA由a指向b
2:如果项目a的点右边是非终结符,那么就得把项目a指向所有项目以非终结符在左边,点在右边第一位的项目。
这里状态1的点右移一位变成状态2,并且状态1的右边为非终结符,所以状态1指向S在左边,右边第一位为点的项目,即3,6,并且添上ε标志。以此类推。后面的子集法什么的和之前都一样。最后构建出DFA


最后看这个叫啥移进-规约矛盾,其实就是出现点在最后一位的时候,不得有其他表达式出现,因为点都在最后一位了,按道理无论输入啥字符,都得进行规约,但是有其他表达式,表示得移进,就冲突了。这里1,4,5都是出现了最后一位有点且出现其他项目的,所以它不是一个LR(0)文法。其实我觉得有点答非所问了,可能答案特别详细吧。
③看下面答案很详细

第六章



这题也不难,首先L->En对应的语义规则就是打印E的值,画树的时候就照着上面画,表示打印结果。
接着按照之前构造语法树一样构造树,只不过是带属性的,假设我们不看带的属性,与之前的语法树就差个digital,这个东西我们可以认为是题目表达式对应的值,也就是说我们按照原来语法树的方法构建出来,最后在每个叶子节点添加digit.lexval作为表达式的值,接着根据那个属性表给每个节点添值就行。

应该老师没讲过
第七章
这一章不想写了,贴大哥写的很通俗易懂大哥的文章



某些年的真题

计算机执行用高级语言编写的程序主要有两种途径:解释和编译
在解释方式下,翻译程序事先并不采用将高级语言程序全部翻译成机器代码程序,然后执行这个机器代码程序的方法,而是每读入一条源程序的语句,就将其翻译成对应其功能的机器代码语句串并执行,然后再读入下一条源程序语句并解释执行,而所翻译的机器代码语句串在该语句执行后并不保留。这种方法是按源程序中语句的动态执行顺序逐句翻译执行的,如果一语句处于一循环体中,则每次循环执行到该语句时,都要将其翻译成机器代码后再执行。
再编译方式下,高级语言程序的执行是分两步进行的;第一步首先将高级语言程序全部翻译成机器代码程序,第二步才是执行这个机器代码程序。因此,编译对源程序的处理是先翻译,后执行。
从执行速度看,编译型的高级语言比解释型的高级语言要快,但解释方式下的人际界面比编译型好,便于程序调试
这两种途径的主要区别在于:解释方式下不生成目标代码程序,而编译方式下生成目标代码程序。
gpt简洁描述
解释方式和编译方式是计算机执行高级语言程序的两种途径。在解释方式下,程序逐条翻译并执行,不生成目标代码。而在编译方式下,程序先完整地翻译成目标代码,然后再执行。解释方式具有交互性和便于调试的优点,但执行速度较慢。编译方式执行速度较快,但不够交互和便于调试。
下面两题差不多

在过程调用中,形式参数是在定义过程时声明的参数,而实际参数是在调用过程时传递给形式参数的具体数值或变量,常见的各种信息见下方答案



用之前的话讲就是该文法存在一个句子,如果有两个不同的最左(最右)推导,则它是二义的。不可判定就是不存在一个算法,他能在有限步骤内,确切判断一个文法是否为二义的。
下面两题也差不多



左边是表格管理,有显示出错处理


好下面用上面的技巧做一套真题的计算题

第一二问没搞手

第三问确实想了半天没找到反例。找反例按道理应该有某个推导式,他会产生终结符与非终结符并列的情况,并且该终结符还可以被推出,但是这里只有(E)他的左边非终结符不能推出,所以它是无二义的。
也许,书上早已经有了答案





最小化(化简):
1:按照是否为终止态分为{0,1,2},{3,4}
2:先看{0,1,2}输入a可得到的集合{1,3},不在上面集合里面,需要划分,发现只有1输入a到3,故1单独划分,此时{0,2},{1},{3,4}。
3:对{0,2}输入a得{1},输入b得{2},都在上面集合里或者是某个集合子集({2}是{0,2}的子集),所以不需要划分,此时{0,2},{1},{3,4}。
4:对{3,4}输入a得{1,3},不在上面集合,需要划分,此时{0,2},{1},{3},{4}结束。
画出最终图:
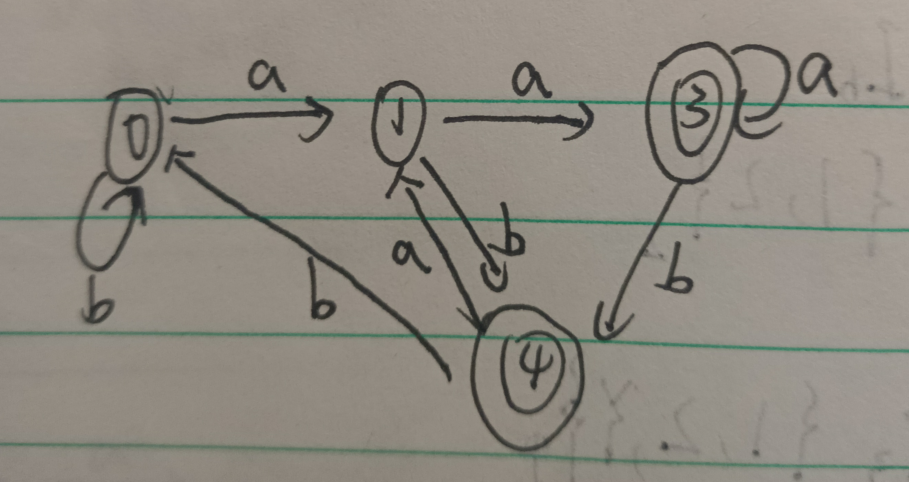
有不同得可以和我讨论一波,自己写还是没有把握

其实这就是之前的题目不过还是贴过来自己说一下

就是关于是否可以划分的问题,我们要注意,集合可以划分就是输入每个出现的字符得到的集合如果出现在当前所有集合某个集合中,或者是某个集合的子集,如果不满足要求就可以划分,例外,其实通过这个找出的不符合的元素也很直观。

①


我们首先一个一个按照规则写完一列,已经确定的我们用勾标记。接着就是看那些非终结符不确定的First集合,其实很简单,看哪些已经推导出来的,比如说P已经推导出来,那么F的也就推导出来了,F的推导出来了,T的就推导出来了,直到每一个都求出来。


和上面差不多,不过首先我们把#加入E的Follow集,我们根据规则先写完一列,再看看有哪些已经求出来的值,这里发现没有一个求出来的值,但是我们注意到,Follow(E’)=Follow(E),代入第一行发现左右两边都有Follow(E),这时我们可以舍掉右边的Follow(E),因为Follow(E)肯定等于Follow(E)嘛,我们就得到{),#},下面的同理

1:观察文法确实没有左递归
2:利用规则二三
我们先找到有产生|这个符号的,然后对他们的First集合做交运算,接着如果某个首选集包含ε,就将产生式左边的非终结符的First集合与Follow集合做交运算。这题我们发现交运算后都是空,所以该文法是LL1文法

算符优先文法满足三个条件:
1:不含产生式ε的产生式
2:没有并列的非终结符
3:满足下面三个关系之一
1.2条件很明显满足,不然怎么让我们建表

首先构建FIRSTVT和LASTVT:




先写出优先级,再画表



可以看到,有的超过了两个关系,所以不是算法优先文法,这里一定要注意,大于小于不要交换左右元素的方向。

①先用增广文法添加一个产生式,再慢慢写

②好可能很多人对第二三问很有疑问,这两个的区别是什么,其实对于之前的答案,是一种不同的求法,但是规则式一样的。项目集规范族其实就是子集法的每个状态的集合的集合 ,只不过作业用NFA的形式,但是我学习了一下,发现没必要那么麻烦,而是通过子集法的规则直接写出这个题目而不用去构造NFA。

项目集规范族:
上面那个就是项目集规范族,构造规则就是将作业那个NFA的规则换个说法。首先看增加的式子D’-> · D,当点的右边是非终结符,我们就把它的产生的候选式前面加个点添加到一个集合里面,这里D-> · CD,D-> · b,因为D-> · CD的点右边是非终结符,所以也要加上C-> · DC,C-> · a,如果发现点右边那个非终结符已经添加过了,就不需要再次添加。接着我们一行一行输入点后面的字符进行状态变化,第一个是 · D,输入D变成D · ,当我们碰到点后面有相同的非终结符的时候,需要加到同一个集合里面,我两条线标记了,C-> · DC的点右边和上面那个一样也是D,所以也添加到I1。
识别活前缀的DFA:
其实我们按照上面的思路构建项目集规范族的时候,已经在构造DFA了,我们所作的就是先把他们框起来再加上箭头和输入字符就成了DFA,这里主要看细节比较繁琐,我就不写了。
其实就是之前的题目换了符号,不过最好动手写一下其他两个怕考

间接三元式就是把重复的用之前的表示,这里去掉第五行,把(6)中的(5)改成(1)
四元式就是自己创造变量,很简单























 1885
1885

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








