dijkstra算法

Dijkstra算法详解

原创已于 2022-10-07 21:01:53 修改 · 403 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #图论 #c++ #笔记

于 2022-10-07 19:58:10 首次发布

本文介绍Dijkstra算法的基本原理及步骤，通过示例演示如何求解图中两点间的最短路径，并提供C++实现代码。

dijkstra算法用于求图的指端路径

dijkstra 是由狄克斯特拉提出的算法，又称迪杰斯特拉算法，在记名字的时候可以通过音译来记

2.步骤：

注：S为走过的顶点， U为没走过的

   （1）刚开始，将所有顶点分为两个顶点集，顶点集S只包含源点v(v就是起始位置，为已经走过的顶点)，
       顶点集U包含除v之外的所有顶点，源点v到U中的顶点x的距离为边上的权(如果x不是v出边的邻接点，则设为∞）
   （2）从U中选取一个顶点u，他是源点v到U中距离最小的一个，然后把顶点u加入顶点集S中
   （3）以顶点u为新考虑的顶点，修改源点v到U中各顶点j的距离，若从源点v到顶点j经过顶点u的距离比之前不经过顶点u的距离更短，则修改源点v到顶点j的最短距离值
   (4)重复2/3步骤，直到U为空即可

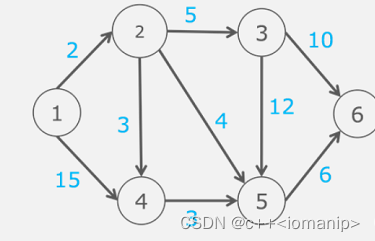
例题

图

题目

输出从点1出发到每一个顶点的最短路径

输入格式：

第一行是2个整数n和m，分别表示图中的顶点个数和边数接下来m行，每行输入3个用空格隔开的数，表示边的起点、终点、边的长度。

输出格式：

n-1行，按照顶点编号从大到小的顺序，每行输出原点1到一个顶点的最短距离的路径。

输入样例：

输出样例：

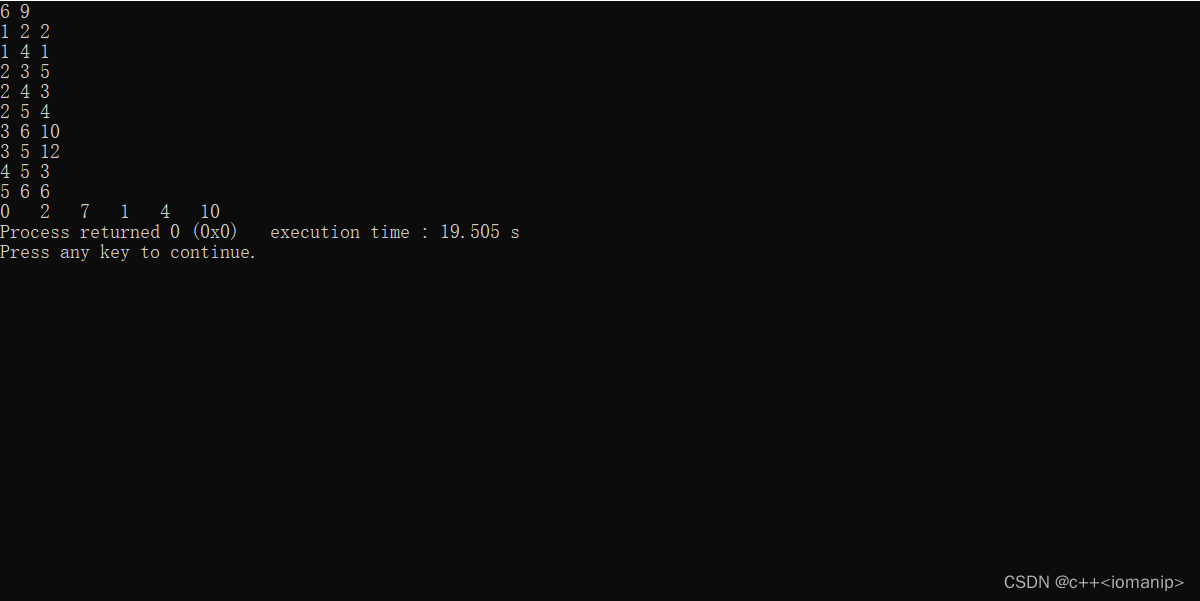
0   2   7   1   4   10

根据dijkstra算法

代码如下

#include <iostream>
#define N 100

int maxV=0x7fffffff;
int n,m,used; 
bool visited[N];
int edge[N][N],dist[N];
using namespace std;


void dijkstra(){
    for(int j=1;j<n;j++){
       int minV=maxV;
       for(int i=1;i<=n;i++){
        if(!visited[i]&&dist[i]<minV){
            minV=dist[i];
            used=i;
        }
       }

    visited[used]=true;
    for(int x=1;x<=n;x++){
        if(edge[used][x]<maxV){
        if(dist[x]>dist[used]+edge[used][x]){
            dist[x]=dist[used]+edge[used][x];
        }
        }
    }
}

}
int main()
{
    // 初始化边的矩阵
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            if(i==j){
                edge[i][j]=0;
            }else{
                edge[i][j]=maxV;
            }
        }
    }

    //输入每条边
    for(int i=1;i<=m;i++){
        int x,y,d;
        cin>>x>>y>>d;
        edge[x][y]=d;
    }
    // 初始化dist数组并标记1节点
    for(int i=1;i<=n;i++){
        dist[i]=edge[1][i];
    }
    visited[1]=true;
    dist[1]=0;

    //调用 -迪杰(狄克).斯特拉算法
    dijkstra();
    for(int i=1;i<=n;i++){
        cout <<dist[i]
        <<"   ";
    }
    return 0;
}

结果如下