机器学习算法（一）基于逻辑回归的分类预测——阿里云天池训练营

1.逻辑回归的介绍和应用

1.1逻辑回归的介绍

分类算法通过对训练样本的学习，得到样本特征到样本标签之间的映射关系，也被称为假设函数，之后利用假设函数对新数据进行分类。
逻辑回归（Logistic regression，简称LR）虽然其中带有"回归"两个字，但逻辑回归其实是一个二分类模型，并且广泛应用于各个领域之中。虽然现在深度学习相对于这些传统方法更为火热，但实则这些传统方法由于其独特的优势依然广泛应用于各个领域中。

1.2线性可分与线性不可分

通常一个分类问题可以分为线性可分与线性不可分俩种
线性可分是指能使用线性组合组成的超平面将两类集合分开（如图1在二维空间可以找到一条直线将不同的类区分开），线性不可分则没有能将两类集合分开的超平面。

对于超平面可以用线性函数表示 :

wx+b=0 w为权重 b 为偏置

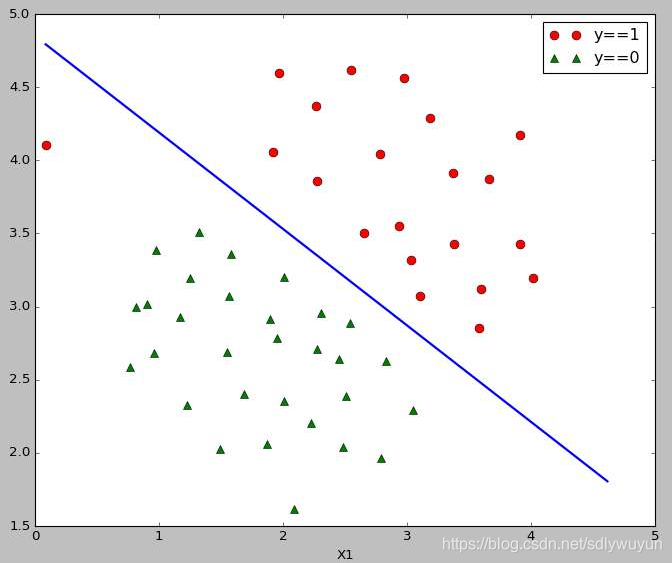
线性可分的特点：低维转高维，还能保持原来的线性可分性的特点；但是高维转低维就不能保持原来的线性可分性
逻辑回归属于广义线性模型，属于线性的分类模型，通过对训练样本的学习可以得到超平面，将数据分为正负俩个类别。用阈值函数将样本映射到不同的类别中，常见的阈值函数有Sigmoid函数

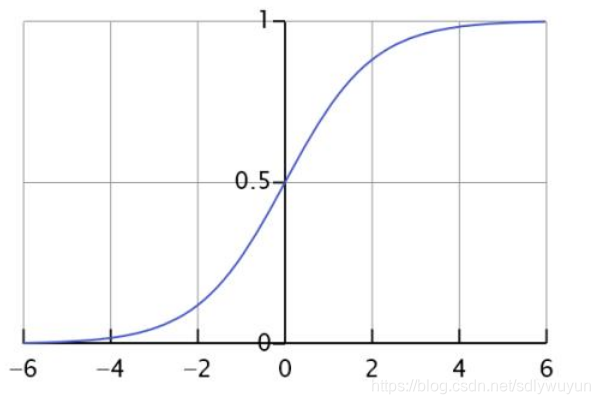
python代码实现：

import numpy as np
def sig(x):
"""sigmoid函数"""
	return 1.0/(1+np.exp(-x))

1.1.3逻辑回归模型的优劣势:
而对于逻辑回归而且，最为突出的两点就是其模型简单和模型的可解释性强。

• 优点：实现简单，易于理解和实现；计算代价不高，速度很快，存储资源低；
• 缺点：容易欠拟合，分类精度可能不高

1.2逻辑回归的应用

逻辑回归模型广泛用于各个领域，包括机器学习，大多数医学领域和社会科学。例如，最初由Boyd 等人开发的创伤和损伤严重度评分（TRISS）被广泛用于预测受伤患者的死亡率，使用逻辑回归 基于观察到的患者特征（年龄，性别，体重指数,各种血液检查的结果等）分析预测发生特定疾病（例如糖尿病，冠心病）的风险。逻辑回归模型也用于预测在给定的过程中，系统或产品的故障的可能性。还用于市场营销应用程序，例如预测客户购买产品或中止订购的倾向等。在经济学中它可以用来预测一个人选择进入劳动力市场的可能性，而商业应用则可以用来预测房主拖欠抵押贷款的可能性。条件随机字段是逻辑回归到顺序数据的扩展，用于自然语言处理。
逻辑回归模型现在同样是很多分类算法的基础组件,比如分类任务中基于GBDT算法+LR逻辑回归实现的信用卡交易反欺诈，CTR(点击通过率)预估等，其好处在于输出值自然地落在0到1之间，并且有概率意义。模型清晰，有对应的概率学理论基础。它拟合出来的参数就代表了每一个特征(feature)对结果的影响。也是一个理解数据的好工具。但同时由于其本质上是一个线性的分类器，所以不能应对较为复杂的数据情况。很多时候我们也会拿逻辑回归模型去做一些任务尝试的基线。