lintcode200 · 最长回文子串（马拉车算法）

最新推荐文章于 2023-03-14 10:18:38 发布

转载最新推荐文章于 2023-03-14 10:18:38 发布 · 194 阅读

1 ·

CC 4.0 BY-SA版权

原文链接：https://zhuanlan.zhihu.com/p/70532099

文章标签：

#java #字符串

Java 同时被 2 个专栏收录

26 篇文章

订阅专栏

leetcode_字符串

14 篇文章

订阅专栏

本文详细介绍马拉车算法（Manacher's Algorithm），这是一种用于寻找字符串中最长回文子串的有效线性方法。文章解释了如何通过在字符间插入特殊符号来统一处理奇数和偶数长度的回文串，并通过示例介绍了算法的核心思想及其实现步骤。

题目描述

在这里插入图片描述
Manacher’s Algorithm 马拉车算法
马拉车算法 Manacher‘s Algorithm 是用来查找一个字符串的最长回文子串的线性方法，由一个叫Manacher的人在1975年发明的，这个方法的最大贡献是在于将时间复杂度提升到了线性。

首先我们解决下奇数和偶数的问题，在每个字符间插入"#"，并且为了使得扩展的过程中，到边界后自动结束，在两端分别插入 “^” 和 “$”，两个不可能在字符串中出现的字符，这样中心扩展的时候，判断两端字符是否相等的时候，如果到了边界就一定会不相等，从而出了循环。经过处理，字符串的长度永远都是奇数了。
在这里插入图片描述
首先我们用一个数组 P 保存从中心扩展的最大个数，而它刚好也是去掉 “#” 的原字符串的总长度。例如下图中下标是 6 的地方。可以看到 P[ 6 ] 等于 5，所以它是从左边扩展 5 个字符，相应的右边也是扩展 5 个字符，也就是 “#c#b#c#b#c#”。而去掉 # 恢复到原来的字符串，变成 “cbcbc”，它的长度刚好也就是 5。
在这里插入图片描述
求原字符串下标
用 P 的下标 i 减去 P [ i ]，再除以 2 ，就是原字符串的开头下标了。

例如我们找到 P[ i ] 的最大值为 5 ，也就是回文串的最大长度是 5 ，对应的下标是 6 ，所以原字符串的开头下标是（6 - 5 ）/ 2 = 0 。所以我们只需要返回原字符串的第 0 到第（5 - 1）位就可以了。

求每个 P [ i ]
接下来是算法的关键了，它充分利用了回文串的对称性。

我们用 C 表示回文串的中心，用 R 表示回文串的右边半径。所以 R = C + P[ i ] 。C 和 R 所对应的回文串是当前循环中 R 最靠右的回文串。

让我们考虑求 P [ i ] 的时候，如下图。

用 i_mirror 表示当前需要求的第 i 个字符关于 C 对应的下标。
在这里插入图片描述
我们现在要求 P [ i ]，如果是用中心扩展法，那就向两边扩展比对就行了。但是我们其实可以利用回文串 C 的对称性。i 关于 C 的对称点是 i_mirror ，P [ i_mirror ] = 3，所以 P [ i ] 也等于 3 。

但是有三种情况将会造成直接赋值为 P [ i_mirror ] 是不正确的，下边一一讨论。

1. 超出了 R
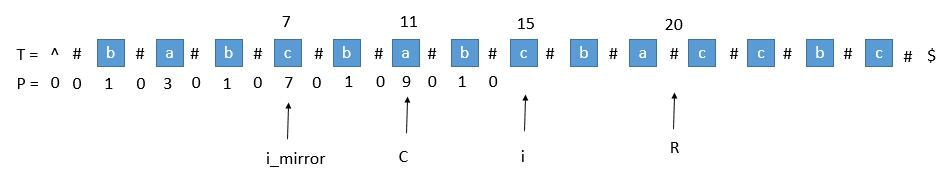
在这里插入图片描述
当我们要求 P [ i ] 的时候，P [ mirror ] = 7，而此时 P [ i ] 并不等于 7 ，为什么呢，因为我们从 i 开始往后数 7 个，等于 22 ，已经超过了最右的 R ，此时不能利用对称性了，但我们一定可以扩展到 R 的，所以 P [ i ] 至少等于 R - i = 20 - 15 = 5，会不会更大呢，我们只需要比较 T [ R+1 ] 和 T [ R+1 ]关于 i 的对称点就行了，就像中心扩展法一样一个个扩展。

2. P [ i_mirror ] 遇到了原字符串的左边界
在这里插入图片描述
此时P [ i_mirror ] = 1，但是 P [ i ] 赋值成 1 是不正确的，出现这种情况的原因是 P [ i_mirror ] 在扩展的时候首先是 “#” == “#” ，之后遇到了 "^"和另一个字符比较，也就是到了边界，才终止循环的。而 P [ i ] 并没有遇到边界，所以我们可以继续通过中心扩展法一步一步向两边扩展就行了。

3. i 等于了 R
就这样一步一步的求出每个 P [ i ]，当求出的 P [ i ] 的右边界大于当前的 R 时，我们就需要更新 C 和 R 为当前的回文串了。因为我们必须保证 i 在 R 里面，所以一旦有更右边的 R 就要更新 R。
在这里插入图片描述
此时的 P [ i ] 求出来将会是 3 ，P [ i ] 对应的右边界将是 10 + 3 = 13，所以大于当前的 R ，我们需要把 C 更新成 i 的值，也就是 10 ，R 更新成 13。继续下边的循环。

java代码实现

    public String longestPalindrome(String s) {
        if ((s == null) || (s.length() == 0))
            return "";
        int n = s.length();
        char[] ch = new char[2 * n + 3];
        Arrays.fill(ch, '#');
        ch[0] = '^';
        ch[2 * n + 2] = '$';
        for (int i = 1; i <= n; i++) {
            ch[2 * i] = s.charAt(i - 1);
        }
        int[] P = new int[2 * n + 3];
        int C = 0, R = 0;
        int i_mirror;
        for (int i = 1; i < 2 * n + 2; i++) {
            i_mirror = 2 * C - i;
            if (i < R)
                P[i] = Math.min(P[i_mirror], R - i);
            else
                P[i] = 0;
            while (ch[i + P[i] + 1] == ch[i - P[i] - 1])
                P[i]++;
            if (i + P[i] > R) {
                R = i + P[i];
                C = i;
            }
        }
        int len = Arrays.stream(P).max().getAsInt();
        int start = (IntStream.range(0, P.length).reduce((i, j) -> P[i] > P[j] ? i : j).getAsInt() - len) / 2;
        return s.substring(start, start + len);
    }