Rectified Flow：生成速度更快

原创已于 2025-12-23 18:34:08 修改 · 507 阅读

10 ·

CC 4.0 BY-SA版权

文章标签：

#生成式 #计算机视觉 #扩散模型

于 2025-12-21 23:20:09 首次发布

扩散模型专栏收录该内容

13 篇文章

订阅专栏

1. 概述

矫正流算法通过因果化（或矫正）插值过程来学习常微分方程作为生成模型，该插值过程平滑地连接噪声和数据。此过程自然倾向于具有更直线轨迹的动力学，从而实现快速的欧拉离散化，并且可以重复进行以进一步提高直线度。

2.生成模型回顾

生成建模可以表述为找到一种计算过程，该过程能够转换噪声分布，成为未知的数据分布。在flow模型中，这一过程可以用常微分方程（ODE）表示：

$\dot{Z}_t = v_t(Z_t), \quad \forall t \in [0,1], \quad {starting from } Z_0 \sim \pi_0, \quad\quad\quad\quad {(1)}$

其中 $\dot{Z}_t = \mathrm dZ_t / \mathrm dt$ 表示时间导数，表示速度场是一个可学习的函数，需要对其进行估计以确保遵循目标分布当从在这种情况下，我们称该随机过程为提供从（ODE）到的传输到。

值得注意的是，除了极少数例外情况外，存在无穷多个从零到零的常微分方程传输方程。到前提是至少存在这样一个过程。因此，明确我们应该优先选择哪种类型的常微分方程至关重要。

一种方法是选择在推理时易于求解的常微分方程。在实践中，通常使用数值方法对常微分方程进行近似，这些方法通常会构建常微分方程轨迹的分段线性近似。例如，欧拉方法就是一种常用的选择：

$\hat{Z}_{t+\epsilon} = \hat{Z}_t + \epsilon v_t(\hat{Z}_t), \quad \forall t \in \{0, \epsilon, 2\epsilon, \dots, 1\}, {(2)}$

在哪里步长。改变步长引入了准确性和计算成本之间的权衡：较小虽然精度更高，但需要更多的计算步骤。因此，我们应该寻找即使使用较大步长也能精确逼近的常微分方程。

图 1.温德米尔夫人扇子图，用于说明欧拉方法轨迹中的误差累积，从不同的初始点开始，随着时间的推移偏离真实解曲线。

理想情况下，常微分方程沿直线轨迹运动，此时欧拉近似的离散误差为零，与步长选择无关。在这种情况下，在时间重参数化之前，常微分方程应满足：

这些常微分方程，被称为直线传输方程，能够实现快速生成模型，并可在单步内完成模拟。我们将由此产生的方程组称为……作为直接耦合和在实践中，我们可能无法实现完美的直线，但我们可以努力使 ODE 轨迹尽可能地直线，以最大限度地提高计算效率。

矫正流RF

构建输送流到假设我们给定一个任意耦合的和由此我们可以获得经验抽样。这可以简单地看作是与定律的独立耦合。正如我们在实践中经常遇到的情况一样，当我们能够获得来自不同来源的独立样本时，这种情况尤为常见。和这个想法是采取并将其转换为由常微分方程模型生成的更优耦合。此外，我们还可以迭代重复此过程，以进一步增强所需的属性，例如直线度。

整流的构建方式如下：

构建插值：

第一步是构建插值过程在两者之间平滑插值和尽管存在多种选择，但我们不妨考虑直线插值这种经典选择：

这里是插值这是一个以“锚桥”方式生成的随机过程：我们首先对端点进行采样。和然后对连接它们的中间轨迹进行采样。

边缘匹配：

根据构造，边缘分布和与目标分布相匹配和通过插值过程。然而，不是像那样的因果常微分方程过程。从而生成输出通过随着时间的推移而不断演进相反，生成需要掌握这两方面的知识。和而不是仅仅从……演变而来作为增加。

如果我们能够转换，这个问题就可以解决。以某种方式将其转化为因果常微分方程过程，同时保持边缘分布不变每次请注意，因为我们只关心输出结果。我们只需要匹配边缘分布即可在每个单独的时间无需匹配轨迹上的联合分布。

或许令人惊讶的是，只需训练速度场即可实现边缘匹配。ODE模型为了匹配斜率通过以下方式进行插值过程：

理论最小值可通过以下方式实现：

这是斜率的条件期望。对于所有经过给定点的插值轨迹如果多条轨迹经过该点速度是平均值对于这些轨迹。

采用标准直线插值法我们有通过求导关于其结果为：

实际上，即使对于大型人工智能模型，(3) 中的优化问题也可以高效求解。参数化方式与现代深度神经网络类似。这是通过利用现成的优化器和随机梯度来实现的，随机梯度是通过抽取配对数据计算得到的。从数据中抽样均匀地然后计算相应的使用插值公式。

符号说明。随机过程是时间的可测量函数。以及一个随机种子（例如，分布）在上述例子中，端点是随机种子，即：斜率由下式给出：作为偏导数就这也是同一个随机种子的函数。损失函数的期望值，完整地写出来是：

在书面表达中，我们经常省略随机种子。每当我们计算期望值时，它都会对括号内的所有随机源进行平均，但明确包含在条件中的随机源除外。

图 2.整流后和蓝线和粉线代表轨迹，颜色根据它们所关联的模式进行着色，以便于可视化。

我们在图 2 中说明了这种直观理解：

在插值过程中不同的轨迹可能存在交点，从而导致多个可能的取值。与同一点相关由于不确定它是从哪条轨迹绘制出来的（图 2a）。
相反，根据常微分方程的定义，更新方向在每个点由以下因素唯一确定：使得 ZtZt 的不同轨迹不可能相交，然后沿不同方向发散。
因此，在这些交点处在哪里不确定且不唯一，常微分方程通过遵循条件期望来“去随机化”更新方向因此，ODE 的轨迹“重新组合”了插值轨迹，从而避免了交叉。参见图 2(b)。
由于 ODE 轨迹 ZtZt 不能相交，它们必须在潜在的交点处弯曲，以“重新连接”原始插值路径并避免交叉。

整流。对于任何时间微分随机过程我们称该 ODE 过程为：

由整流引起的我们将其表示为：

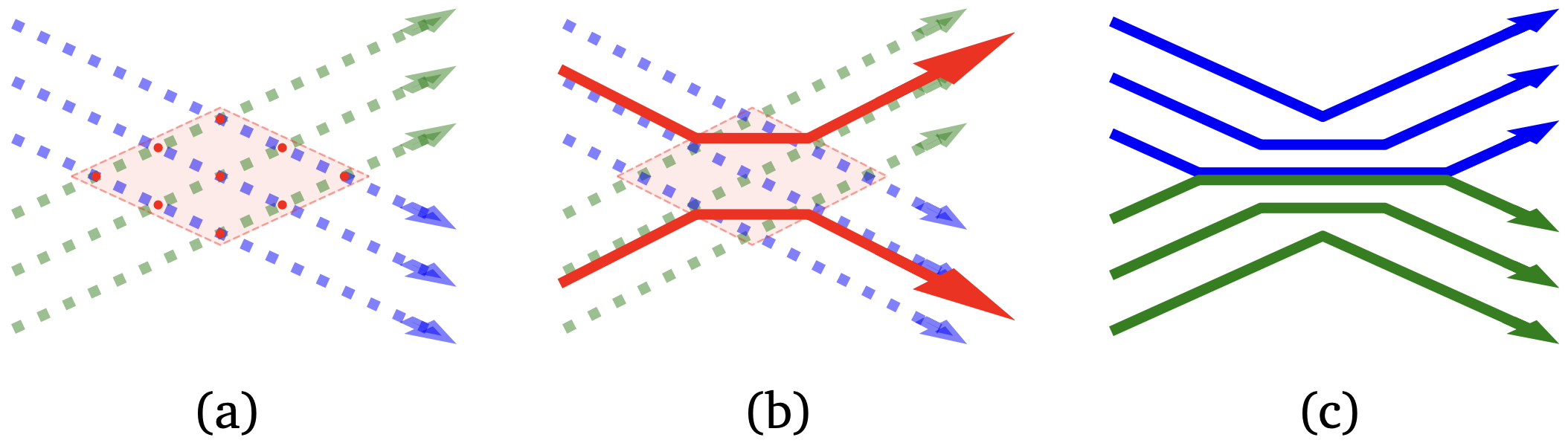
近距离观察整流如何重塑插值轨迹

图 3.整流如何“重塑”插值轨迹的特写视图。(a) 带有交点的插值轨迹。(b) 交点处的平均速度方向（红色箭头）。(c) 整流后的流轨迹。

图 3 展示了整流如何“重塑”插值轨迹的特写视图。考虑两束相交的插值轨迹，它们形成“混淆区域”（中间的阴影区域）。在该区域内，沿整流后的方向运动的粒子将遵循平均方向。粒子离开该区域后，会根据其出口侧加入到原始插值流之一并继续运动。由于矫正后的流轨迹在该区域内不会相交，它们保持分离状态，并从各自的出口侧离开，从而有效地“重新连接”了原始插值轨迹。

是什么造就了整流它的优点在于它保留了边缘分布在每个点上都实现了“更好”的耦合就最佳运输而言：

边缘保存

这及其整流在每个时间点都具有相同的边缘分布，那是：

在哪里表示随机变量的概率分布（或规律）。

直观地说，根据定义在（1）中，根据动力学，进入和流出空间中每个无穷小体积的总质量流量相等。和这样就确保了即使流动方向不同，这两个过程也能产生相同的边缘分布。
运输成本

起始-结束对来自整流的保证运输成本不会高于同时，对于所有凸成本函数：

直观地说，这是因为根据三角不等式，解开交点可以减少轨迹的长度：